Als Filter werden Schaltungen bezeichnet, die auf ein frequenzabhängiges Übertragungsverhalten ausgelegt sind, um das Spektrum eines Eingangssignals in einer gewünschten Weise zu formen. Sie besitzen vielfältige Anwendungsbereiche in der Signalverarbeitung. Die vier Grundtypen sind Tief- und Hochpass, sowie Bandpass- und Bandsperrfilter. In der Hochfrequenztechnik kommen verschiedene Realisierungsformen zum Einsatz. Neben den Filtern aus konzentrierten Bauelmenten (Spulen und Kondensatoren) werden auch verteilte Bauelemente in Form von Leitungsstücken eingesetzt.

Filterarten [Bearbeiten]

Tiefpass

Der Tiefpass ist ein Filter, der Signalanteile mit Frequenzen unterhalb einer Grenzfrequenz passieren lässt, Signalanteile oberhalb einer Grenzfrequenz werden dagegen blockiert. Die Realisierung passiver analoger Tiefpässe erfolgt durch passive Bauelement, wie Widerständen, Spulen und Kondensatoren. Durch schaltungstechnische Erweiterungen um aktive Bauelemente wie Operationsverstärker oder Transistoren können aktive analoge Tiefpässe realisiert werden. Unterschieden wird hierbei zwischen dem idealem und realen Tiefpass.

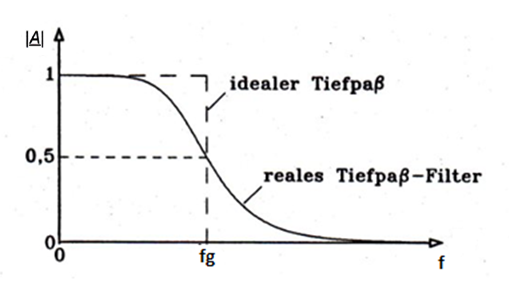
Ein idealer Tiefpass lässt die Eingangsspannung unterhalb der Grenzfrequenz $$f_g$$  unverändert durch, oberhalb dieser Grenzfrequenz wird die Eingangsspannung vollständig gesperrt. Der ideale Tiefpass ist jedoch nur ein Modell, dem man sich in einer Realisierung zu nähern versucht. Diese Annäherung wird durch den realen Tiefpass beschrieben.

Die folgende Abbildung soll den Amplitudengang eines idealen bzw. realen Tiefpasses zeigen:

Passiv analoger Tiefpass

Da der passive analoge Tiefpassfilter, wie sein Name schon sagt, aus passiven Bauelementen wie z.B. Widerständen, Spulen und Kondensatoren realisiert wird, besitzt dieser keine wirkende Verstärkungsfunktion.

RC-Tiefpass 

Im einfachsten Fall besteht ein Tiefpass aus einem Widerstand und einem Kondensator, dem sog. RC-Glied. Der RC-Tiefpass stellt einen Filter mit 1. Ordnung in folgender Anordnung dar:

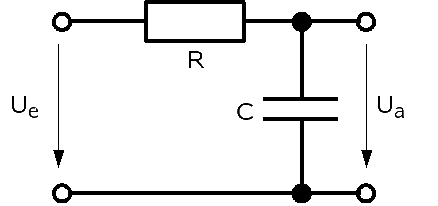
Übertragungsfunktion

Gemäß der Spannungsteilerregel folgt einer sinusförmigen Eingangsspannung mit der Frequenz $$f$$ wieder eine sinusförmige, jedoch frequenzabhängige Ausgangsspannung:

$$U_a= U_{\rm{e}} \left \frac{{\vert X_c \vert}} {\sqrt{X^2_c+R^2}}$$

dabei bezeichnet $$U_e$$ und $$U_a$$ die Beträge der Ein- bzw. Ausgangsspannungen,

$$\vert X_c \vert= \frac{{1}} {\omega C}}$$ beschreibt den Betrag des Blindwiderstands des Kondensators und $$\omega= 2 \pi f$$ die Kreisfrequenz.

Damit ergibt sich für die Übertragungsfunktion eines RC-Tiefpasses folgende Beziehung:

$$ \frac{{U_a}} {{U_e}}= \frac{1}{\sqrt{1+(2 \pi f R C)^2}}$$

mit $$ \tau= RC$$ als Zeitkonstante des RC-Glieds.

Die Gleichung zeigt, dass sich bei niedrigen Frequenzen $$f$$  das Verhältnis $$U_a$$ zu $$U_e$$ annähernd eins wird:

 für $$f \to0$$ wird $$ R^2 (2 \pi f C)^2 << 1$$ daraus folgt:  $$ \frac{{U_a}} {U_e}} \approx1$$ 

Bei steigender Frequenz hingegen wird die Ausgangsspanunng $$U_a$$ nahezu Null:

für $$f \to \infty$$ wird $$ \frac{{U_a}} {U_e}} \approx \frac{{1}} {\infty}} \approx0$$ daraus folgt: $$U_a \to0$$

Der Übergang dieser beiden Frequenzbereiche wird Grenzfrequenz genannt und ist mit

$$ \frac{{U_a}} {U_e}}= \frac{{1}} {\sqrt{2}}$$ oder $$ U_a= \frac{{U_e}}{\sqrt{2}} \approx U_e \cdot0{,}707$$ definiert (d. h. $$U_a$$  ist gegenüber $$U_e$$  um 3 dB abgeschwächt). Bei Frequenzen, die exakt der Grenzfrequenz entsprechen, sind die Werte des Blind-und Wirkwiderstands gleich. Diese Frequenz lässt sich durch folgende Formel bestimmen:  $$f_g= \frac{{1}} {2 \pi R C}}$$.

RL-Tiefpass

Die Realisierung eines Tiefpasses 1. Ordnung mit Hilfe des RL-Gliedes stellt folgende Anodnung dar:

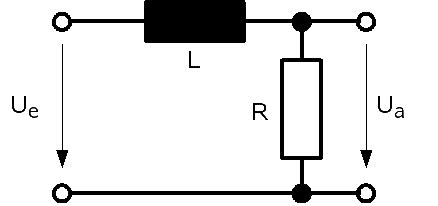
Übertragungsfunktion

Gemäß der Spannungsteilerregel folgt:

 $$U_a= U_{\rm{e}} \left \frac{{R}} {\sqrt{R^2 + X^2_L}}$$

dabei bezeichnet $$U_e$$ und $$U_a$$ die Beträge der Ein- bzw. Ausgangsspannungen,

$$X_L= \omega \cdot L$$ beschreibt den Betrag des Blindwiderstands der Induktivität und $$\omega= 2 \pi f$$ die Kreisfrequenz.

Damit ergibt sich für die Übertragungsfunktion eines RL-Tiefpasses folgende Beziehung:

$$ \frac{{U_a}} {{U_e}}= \frac{1}{\sqrt{1+ \frac{(2 \pi f \cdot L)^2}{R^2}}$$

mit $$ \tau= L/R$$ als Zeitkonstante des RL-Glieds.

Die Gleichung zeigt, dass sich bei niedrigen Frequenzen $$f$$  das Verhältnis $$U_a$$ zu $$U_e$$ annähernd eins wird:

für $$f \to0$$ wird $$ (\frac{2 \pi f \cdot L}{R})^2<< 1$$ daraus folgt:  $$ \frac{{U_a}} {U_e}} \approx1$$

Bei steigender Frequenz hingegen wird die Ausgangsspanunng $$U_a$$ nahezu Null:

für $$f \to \infty$$ wird $$ \frac{{U_a}} {U_e}} \approx \frac{{1}} {\infty}} \approx0$$ daraus folgt: $$U_a \to0$$

Grenzfrequenz : $$f_g= \frac{{R}} {2 \pi L}}$$

 Amplitudengang: $$H(\omega)= \frac{\hat u_a}{\hat u_e}= \frac{1}{\sqrt{1+  (\frac{\omega L}{R})^2}}$$

 Phasengang:  $$\phi(\omega)= -\arctan( \frac {\omega L}{R})$$

Tiefpass 2. Ordnung

Für die Realisierung eines Tiefpasses 2. Ordnung wird zu dem Wirkwiderstand R eine Induktivität L in Reihe geschaltet. Durch den zusätzlichen Energiespeicher wird der Tiefpass in seiner Wirkung stärker.

Passiver Tiefpass 2. Ordnung:

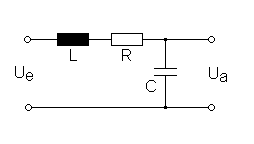
Übertragungsfunktion

$$H(\omega)= \frac{U_a}{U_e}= \frac{\vert X_C\vert}{\sqrt{R^2+ (X_L+ X_L)^2}}$$

mit $$ X_L= \omega L$$ , $$ X_C= - \frac{1}{\omega C}$$ und  $$ \omega= 2\pi f$$

$$H(\omega)= \frac{1}{\sqrt{\omega^4 L^2 C^2+\omega^2 R^2 C^2- 2\omega^2 L C +1}}$$

Tiefpass n-ter Ordnung

Tiefpässe höherer Ordnungen erreicht man durch das hintereinanderschalten von mehreren Tiefpässen. Zwei hintereinandergeschaltete
Tiefpässe 2. Ordnung bilden einen Tiefpass 4. Ordnung. Allgemein werden zur Realisierung von Tiefpassfilter n-ter Ordnung n speichernde Elemente, wie Kondensatoren oder Spulen benötigt.

Aktiv analoger Tiefpass

Aktive Tiefpassfilter können durch mehrstufige Breitbandverstärker und einem frequenzabhängigen Rückkopplungsfaktor realisiert werden. Als Breitbandverstärker kommen Operationsverstärker zum Einsatz. Beim Aufbau des Rückkopplungsnetzwerkes werden RC Komponenten verwendet.

Aktiver Tiefpass 1. Ordnung:

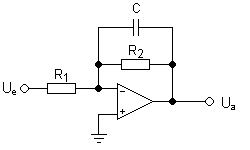
Übertragungsfunktion

$$U_a= -U_{\rm{e}} \left \cdot \frac{R_2}{R_1} \cdot \frac{{\vert X_c \vert}} {\sqrt{X^2_c+R^2}}$$

Grenzfrequenz

$$f_g= \frac{{1}} {2 \pi (2 \cdot R \cdot C)}}$$

Bei der Grenzfrequenz ist die Verstärkung $${R_2}/{R_1}$$ auf das $${1}/{\sqrt{2}}$$-fache der Gleichspannungsverstärkung abgefallen.

Hochpass

Das Hochpass-Filter lässt im Idealfall Signale oberhalb einer gewählten Grenzfrequenz ungehindert, also ohne die Amplitude zu dämpfen, passieren und dämpft Signale unterhalb der Grenzfrequenz. Während beim idealen Hochpass ist dies wie auch beim idealen Tiepass in Form einer Schrittfunktion. Zieln einer Realisierung kann also eine möglichst steile Flanke sein. Bei der Auslegung des Filters müssen die Unterschiede zwischen einem idealen und einem realen Filter berücksichtigt werden, da sonst Teile des Signals gedämpft werden könnten.

Passiver Hochpass

Das passive Hochpass-Filter wird üblicherweise als RC- oder RL-Filter realisiert. In der Schaltungstechnik wird meist das RC-Filter gewählt, da eine Spule zu viel Platz auf einer Platine benötigt. Wie Name bereits vermuten lässt werden nur passive Elemente verwendet, wordurch das Filter ein Eingangssignal nicht verstärken kann. Für die Ordnung n=1 besteht das Filter aus 2 Elementen. Mit Erhöhung der Ordnung kann eine steilere Flanke erzeugt werden, die benötigt wird um z.B. Frequenzen, die nahe beieinander liegen trennen zu können.

Die einfachste Realisierung eines Hochpass-Filters sieht wie folgt aus:

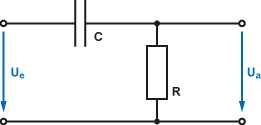
Der Filter lässt sich relativ einfach dimensionieren, indem die gewünschte Grenzfrequenz eingesetzt und ein Elementwert vorgegeben wird.

$$f_{g}= \frac{1}{2 \cdot \pi \cdot R \cdot C} $$

Die Herleitung der Übertragungsfunktion geschieht analog zum Tiefpass-Filter.

Aktiver Hochpass

Ein aktives Filter ist in der Lage, neben dem Filtern von Signalanteilen, das eigentliche Signal zu verstärken. Dieses Filter kann auf zwei Arten realisiert werden. Zum einen kann einfach hinter ein passives Filter ein Operationsverstärker als Impedanzwandler zwischengeschaltet werden. Dadurch erhält man die gewünschte Verstärkung und kann verhindern, dass die Eigenschaften des RC-Filters durch eine Belastung am Ausgang geändert werden.

Auf dem Bild befindet sich fälschlicherweise ein Tiefpass, allerdings ist das Prinzip für ein Hochpass-Filter das selbe. Über R₂ und R₃ kann eine Verstärkung gewählt werden. Der Hochpass vor dem Operationsverstärker bestimmt über die Grenzfrequenz der Schaltung.

Verstärkung: $$A= \frac{R_{2}+R_{3}}{R_{3}} $$

Die andere Möglichkeit besteht darin, den Filter in der Rückkopplung des Operationsverstärkers zu integrieren.

Dimensionieren lässt sich dieses Filter, indem C1, die Grenzfrequenz und die negative Gleichspannungsverstärkung A_∞ vorgeben werden. Mit diesen Vorgaben können R1 und R2 mit:

$$R_{1}= \frac{1}{2 \cdot \pi \cdot f_{g} \cdot a_{1} \cdot C_{1}} $$ und $$R_{2}=-\left(R_{1}\right) \cdot A_{\infty}$$

bestimmt werden. a1 ist ein Koeffizient, der je nach Filtertyp (Butterworth, Tschebyscheff, ...) gewählt wird. Dieser kann aus der Tabelle der Filterkoeffizienzen, z.B. aus [6], entnommen werden.

Aktiver Hochpass n-ter Ordnung

Höhere Ordnungen können durch Verschalten der Filter 1. und 2. Ordnung erreicht werden. Die Frequenzgänge der einzelnen Stufen werden dabei multipliziert. Es ist nicht möglich jede Stufe für eine Grenzfrequenz zu berechnen und diese dann zu verschalten. Das dabei entstehende Übertragungsverhalten wäre ein anderes. Es ist nötig jede Stufe so einzustellen, dass der Gesamtfilter das gewünschte Verhalten besitzt.

Die obere Abbildung zeigt die Realisierung eines aktiven Hochpassfilters zweiter Ordnung.

Bandpass

Der Bandpass ist ein Filter, welcher Signale innerhalb eines Frequenzbereiches passieren lässt. Unterhalb sowie oberhalb dieses Durchlassbereiches werden die Signalanteile unterdrückt. Unterschieden wird hierbei zwischen idealem und realem Bandpass.Die Realisierung eines Bandpasses erfolgt je nach Anwendungsgebebiet aktiv oder passiv mittels Leiterbahnen oder elektronischen Bauteilen.

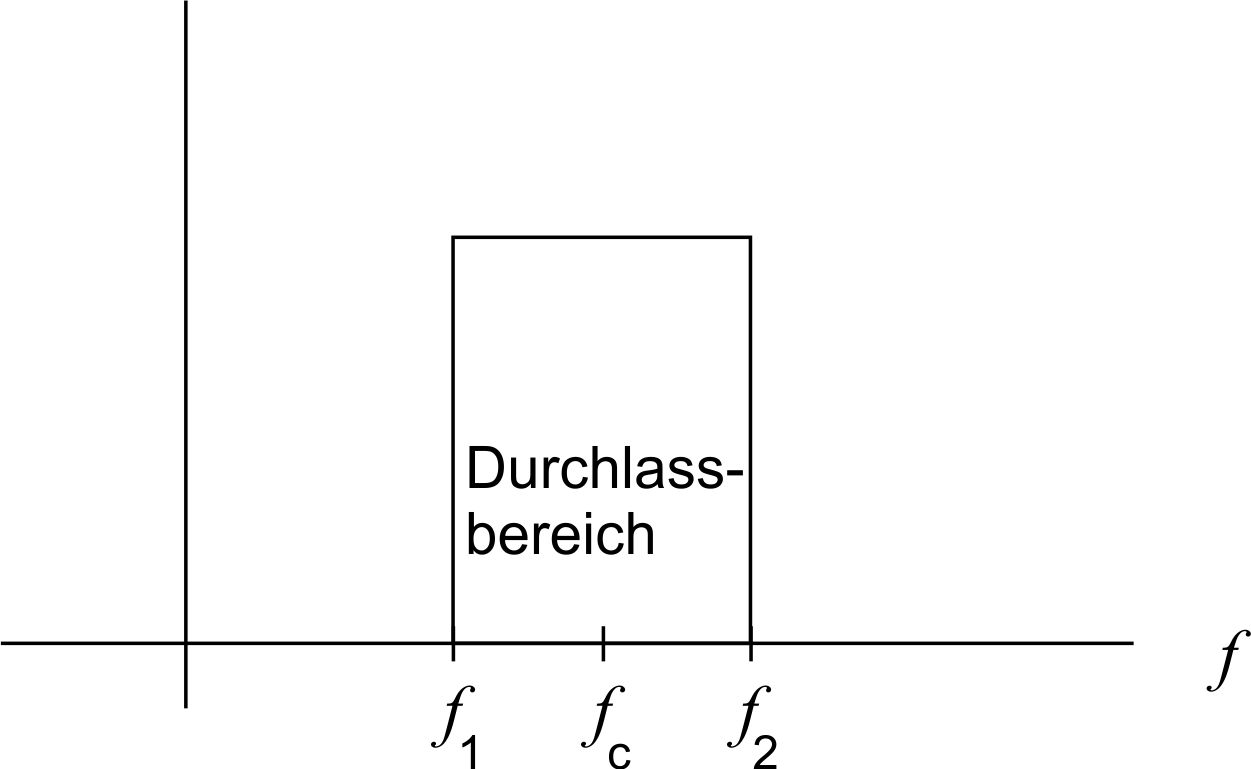
Der ideale Bandpass

Bei einem idealen Bandpass werden die Signale verzerrungsfrei in einem Frequenzbereich übertragen. Das heißt die Übergänge von Sperr in den Durchlassbereich bzw. auch umgekehrt sind abrubt, da das Filter im Sperrbereich durch eine unendlich hohe Dämfung und im Durchlassbereich durch keine Dämpfung charakterisiert ist. Desweiteren handelt es sich bei einem idealen Bandpass um ein nichtkausales System, da seine Impulsantwort bereits einsetz bevor das Eingangssignal eintrifft.

Übertragungsfunktion

Unter der Vorraussetzung, dass die Mittenfrequenz mindestens doppelt so groß ist wie die Bandbreite gilt für die Übertragungsfunktion eines idealen Bandpasses:

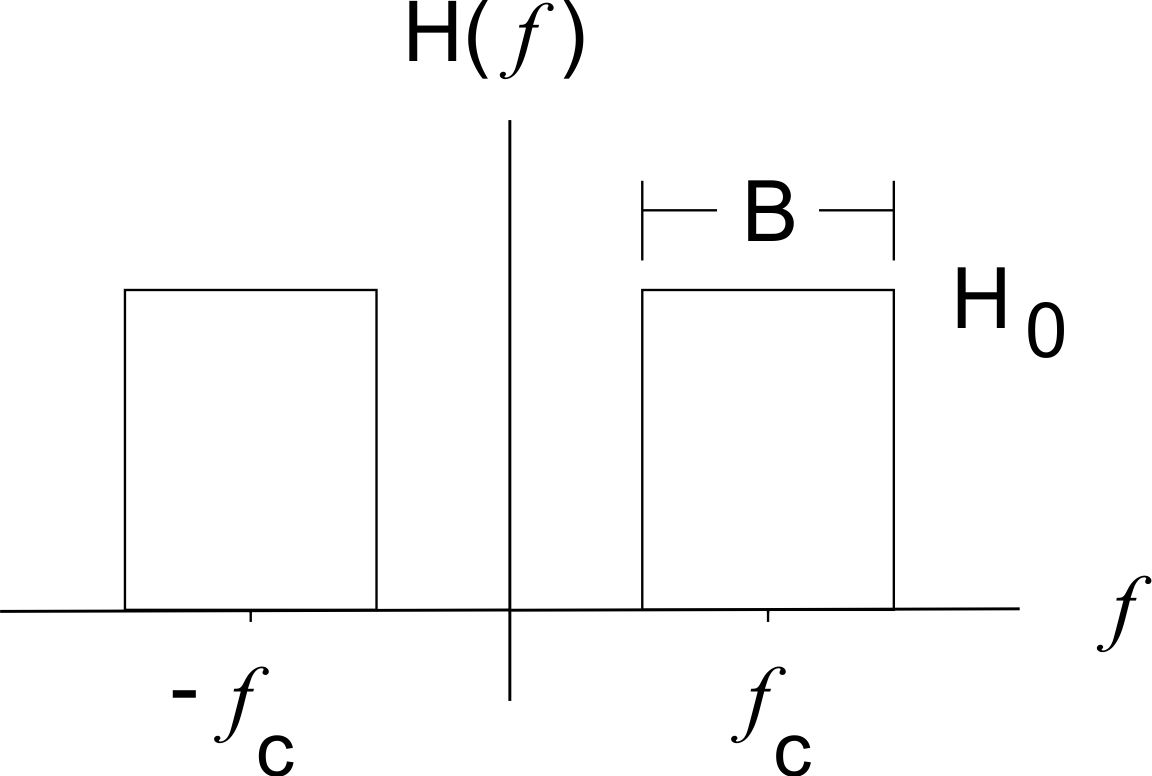
$$H(f) =  H_{\rm{0}} \left( rect\frac{\left( f-f_{\rm{c}}\right)}{B}+rect\frac{\left( f+f_{\rm{c}}\right)}{B}\right)$$


Wobei B die Breite des Durchlassbereiches, $$f_{\rm{c}}$$ die Mittenfrequenz und $$H_{\rm{0}}$$ die Amplitude beschreiben.

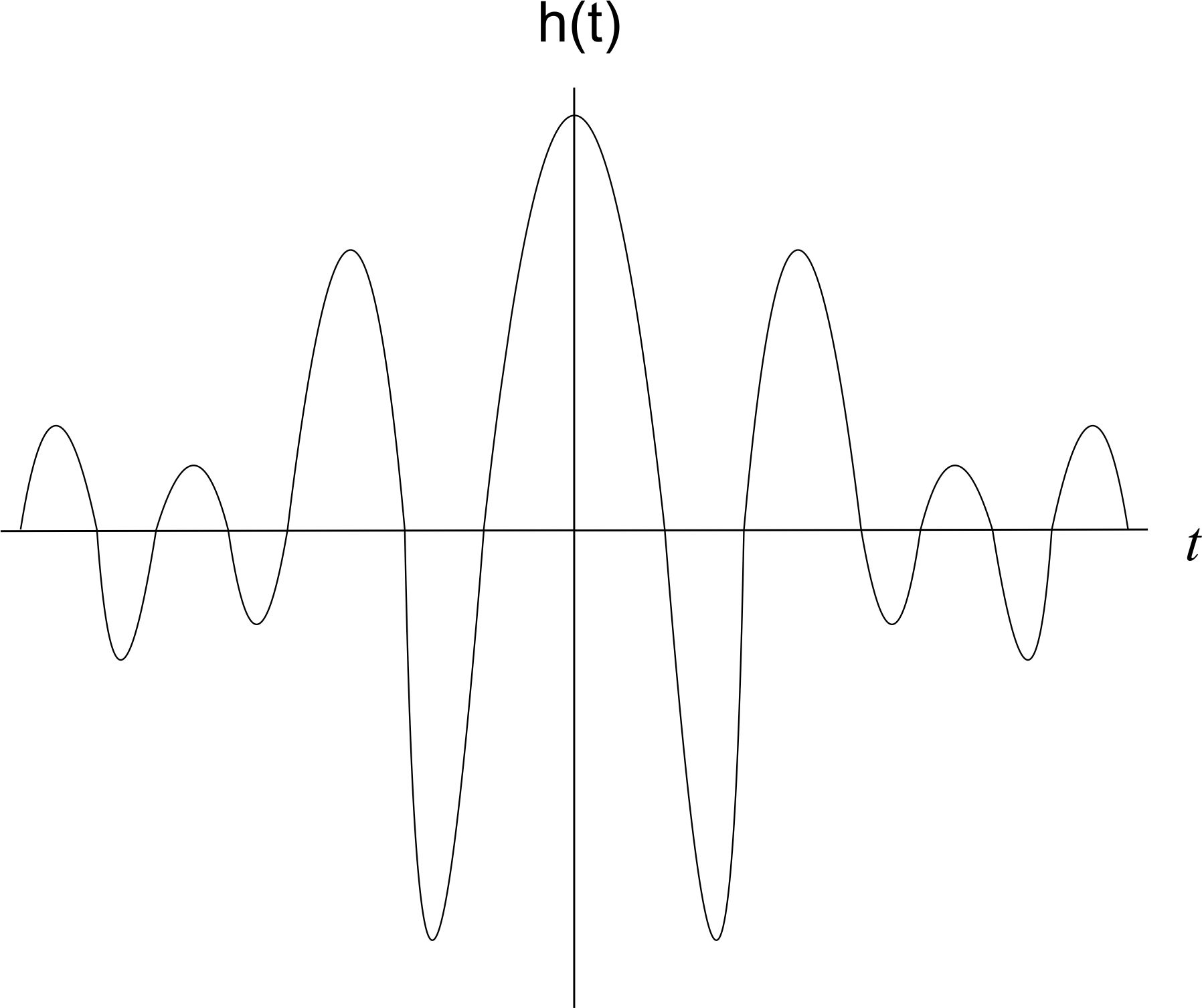
Impulsantwort

Die Impulsantwort eines idealen Bandpasses lässt sich aus der Übertragungsfunktion ableiten. Die Übertragungsfunktion lässt sich dabei als rect-Funktion darstellen, welche im Ursprung verschoben ist.

$$H(f) =  H_{\rm{0}}rect\left( \frac{f}{B}\right)\ast [ \delta\left( f-f_{\rm{c}}\right)+\delta\left( f+f_{\rm{c}}\right)]$$


Unter Zuhilfenahme des Faltungstheorems, der Fourier-Transformierten, der rect-Funktion, des Dirac Impulses und des Verschiebungstheorems folgt:

$$h(t) = \mathfrak{J}^{-1} \{  H_{\rm{0}}rect\left( \frac{f}{B}\right)\} \mathfrak{J}^{-1} \{  \delta\left( f-f_{\rm{c}}\right)+\delta\left( f+f_{\rm{c}}\right)\}$$

$$h(t) = H_{\rm{0}}Bsin(\pi Bt)(e^{j2\pi f_{\rm{c}}t}+e^{-j2\pi f_{\rm{c}}t})$$

$$h(t) = H_{\rm{0}}rect\left( \frac{f}{B}\right) \left( \delta\left( f-f_{\rm{c}}\right)+\delta\left( f+f_{\rm{c}}\right)\right)$$



$$h(t) = 2H_{\rm{0}}B si \left( 2\pi Bt \right)cos\left( 2\pi f_{\rm{c}} t \right) $$

Der reale Bandpass

Bei einem realen Bandpass werden die Signale nicht komplett verzerrungsfrei in einem Frequenzbereich übertragen. Das heißt die Übergänge von Sperr in den Durchlassbereich bzw. auch umgekehrt sind nicht so abrubt wie bei einem idealen Bandpass, da das Filter im Sperrbereich nicht mehr durch eine unendlich hohe Dämfung und im Durchlassbereich durch keine Dämpfung charakterisiert ist.

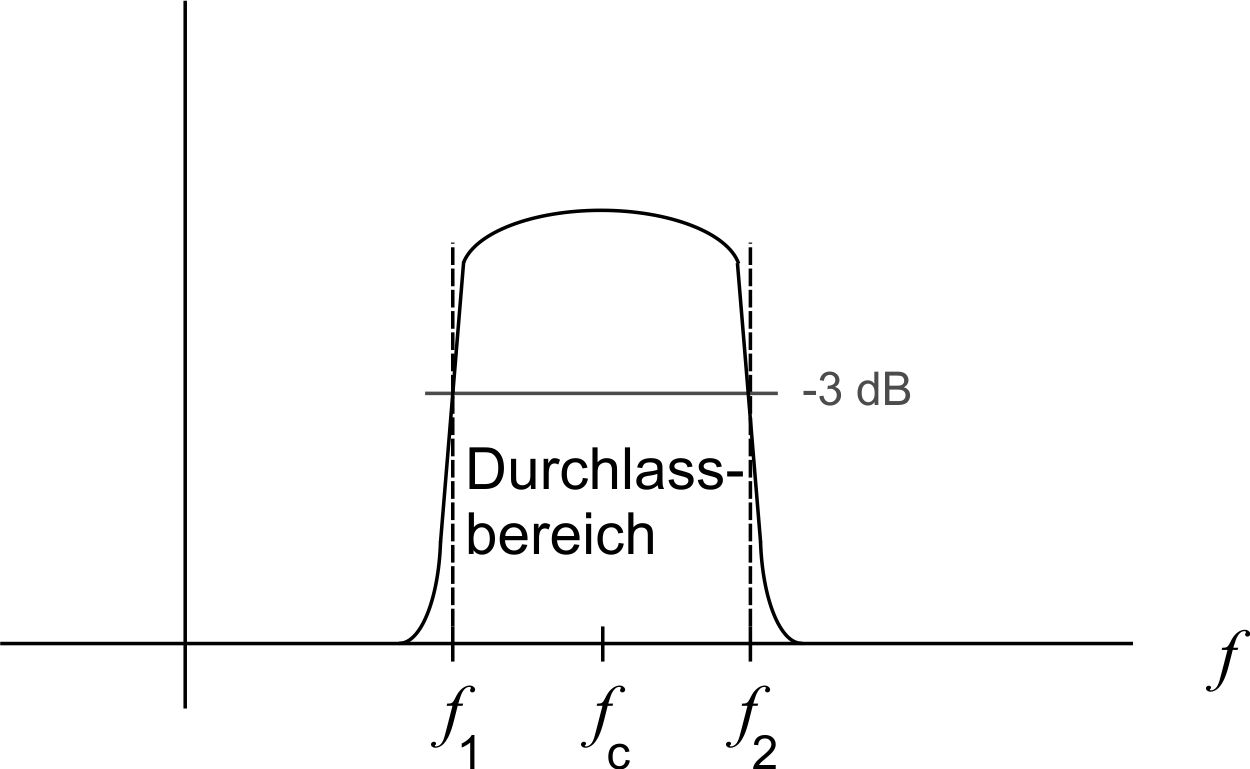
Üblicherweise werden bei Filtern die Kenngrößen anhand der 3dB-Eckfreqeunzen festgemacht. Dabei erfolgt eine Reduktion um 3dB am Übergang zwischen dem Sperrbereich und dem Durchlassbereich.

Die Bandbreite B des Filters entspricht der Breite des Durchlassbereiches und kann als Differenz zwischen der oberen Grenzfrequenz $$ f_2 $$ und der unteren Grenzfrequenz $$ f_1 $$ dargestellt werden:

$$B=f_2-f_1$$

Die Mittenfrequenz $$ f_c $$ die auch als Resonanzfrequenz bezeichnet wird ist wie folgt definiert:

$$f_c=\sqrt{f_2f_1}$$

Realisierungsmöglichkeiten

Passiver Bandpass

Die einfachste Realisierungsmöglichkeit eines Bandpasses besteht in der Kombinationen von Widerständen (R), Spulen (L), Kondensatoren (C).
Da diese Bauelemente keine externe Spannungsversorgung benötigen, werden sie als passive Bauelemente bezeichnet.
Die Anzahl der verwendeten Bauteile richten sich dabei nach der geforderten Güte des Bandpasses.
Meistens ist eine hohe Güte gewünscht, um einen scharfen Übergang der Übertragungsfunktion vom Durchlass- in den Sperrbereich zu ermöglichen.

Aktiver Bandpass

Bei der Realisierung eines aktiven Bandpasses werden neben den passiven Bauteilen zusätzlich noch aktive Bauteile wie z. B. Transistoren oder Operationsverstärker verwendet. Diese aktiven Komponenten benötigen im Gegensatz zu den passiven stets eine externe Spannungsversorgung. Wodurch sie zugleich eine Verstärkung des Signals bewirken können, sodass sie Filter und Verstärker in Einem darstellen.

Ordnungen

Bandpässe weisen mindestens eine Filterordnung von zwei auf.

In der Skizze ist ein Bandpass 2. Ordnung als elektrisch passives Filter dargestellt.

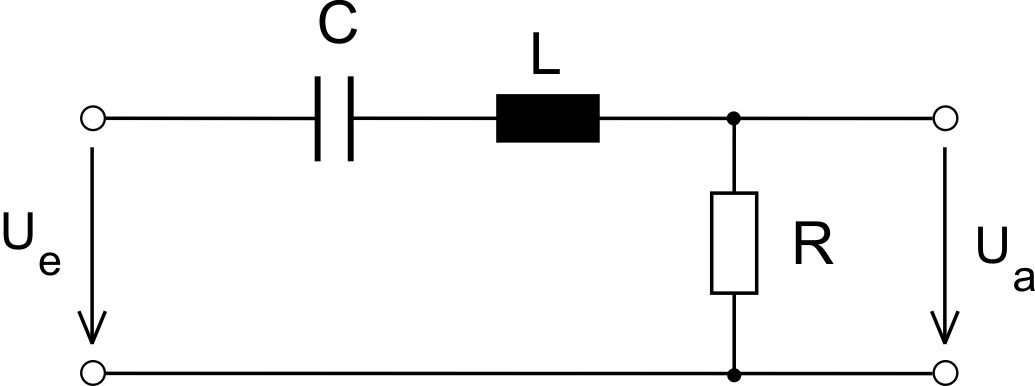
Die dazu gehörige Übertragungsfunktion lautet:

$$H(s) = \frac{sRc}{1+sRC+s^2LC}$$

Eine weitere Größe ist der Gütefaktor. Dieser lautet bei einem Bandpass 2.Ordnung:

$$Q = \frac{f_c}{B}  = \frac{1}{R} \sqrt{ \frac{L}{C}}$$

Bandpässe höherer Ordnung können durch Verkettung einzelner Hoch- und Tiefpässe relisiert werden.

Bandsperre

Die Bandsperre ist das Gegenteil von einem Bandpass. Dabei werden alle Frequenzen ungedämpft übertragen mit Ausnahme eines schmalen Frequenzbereiches. Unterschieden wird hierbei zwischen idealer und realer Bandsperre sowie aktiver und passiver.

Die ideale Bandsperre

Bei einer idealen Bandsperre sind die Übergänge von Sperr- in den Durchlassbereich verzerrungsfrei.

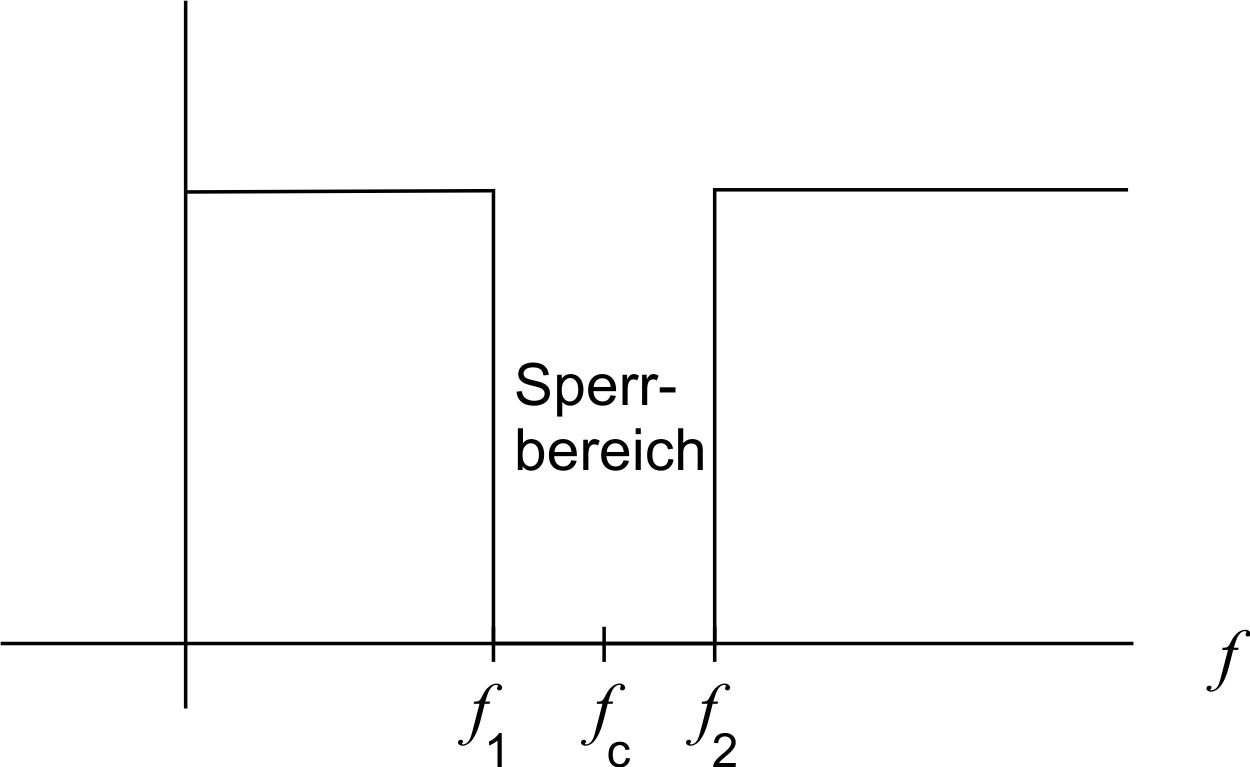
Die reale Bandsperre

Bei der realen Bandsperre sind die Übergänge von Sperr in den Durchlassbereich bzw. auch umgekehrt nicht so abrubt wie bei einem idealen Bandpass. Die folgende Abbildung verdeutlicht dies:

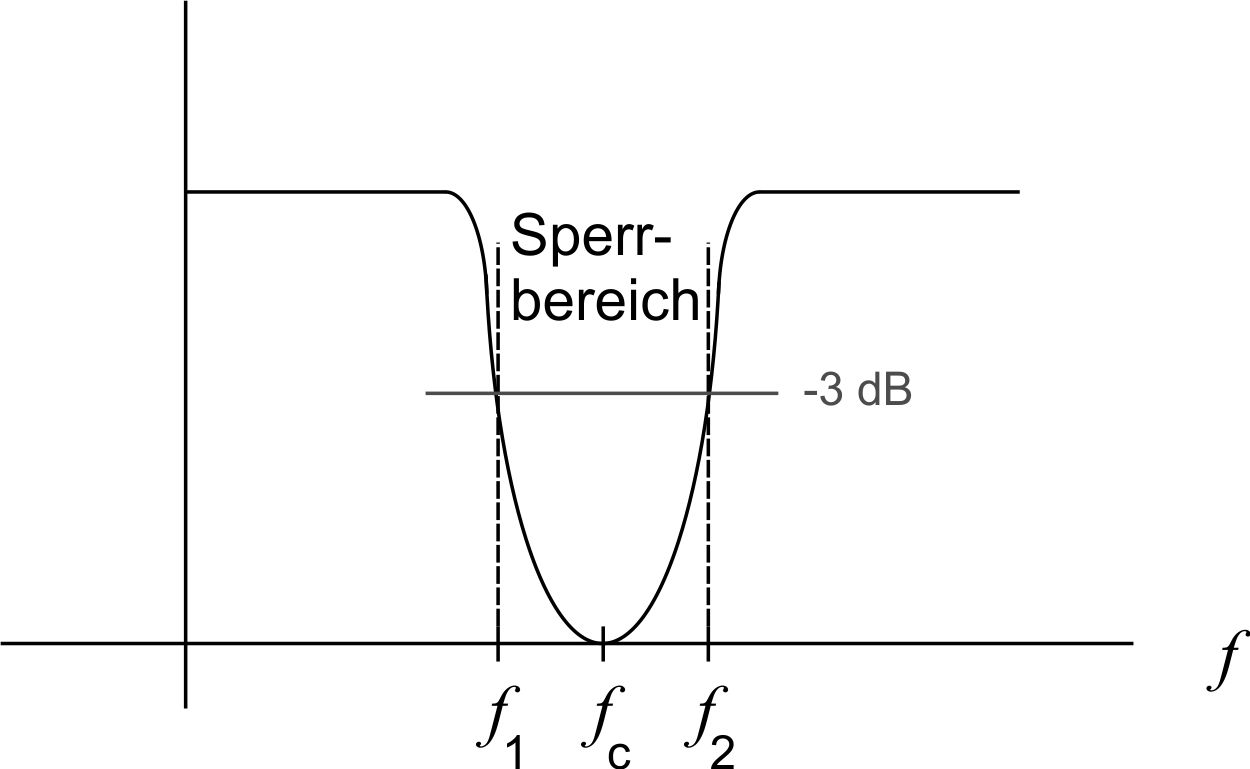
Bei einer Bandsperre ist die Bandbreite im Sperrbereich schmal. Oft werden Filter mit sehr hohen Flankensteilheiten benutzt, deren Bezeichnung Notch-Filter lauten. Anwendung finden Bandsperrfilter unter anderem um bestimmte Störfrequenzen aus einem Audio-Signal oder Netzbrummgeräusche zu entfernen.

Realisierungsmöglichkeiten

Passive Bandsperre

Die einfachste Realisierungsmöglichkeit eines Bandpasses besteht in der Kombinationen von Widerständen (R), Spulen (L), Kondensatoren (C).Die folgende Abbildung zeit eine RC-Bandsperre 2-ter Ordnung :

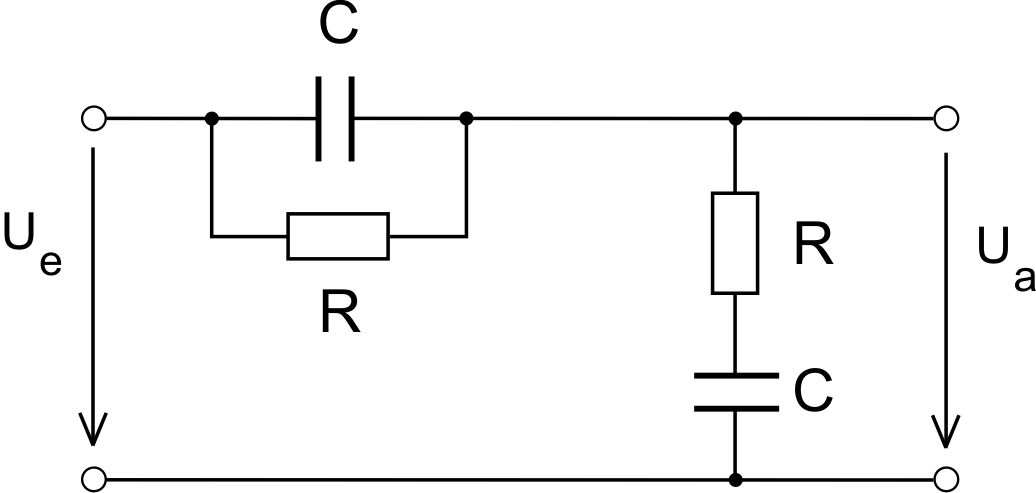
Aktive Bandsperre

Bei der Realisierung eines aktiven Bandpasses werden neben den passiven Bauteilen zusätzlich noch aktive Bauteile wie z. B. Transistoren oder Operationsverstärker verwendet. Ein Beispiel für eine aktive Bandperre stellt der Notch-Filter da, der in folgernder Abbildung dargestellt ist:

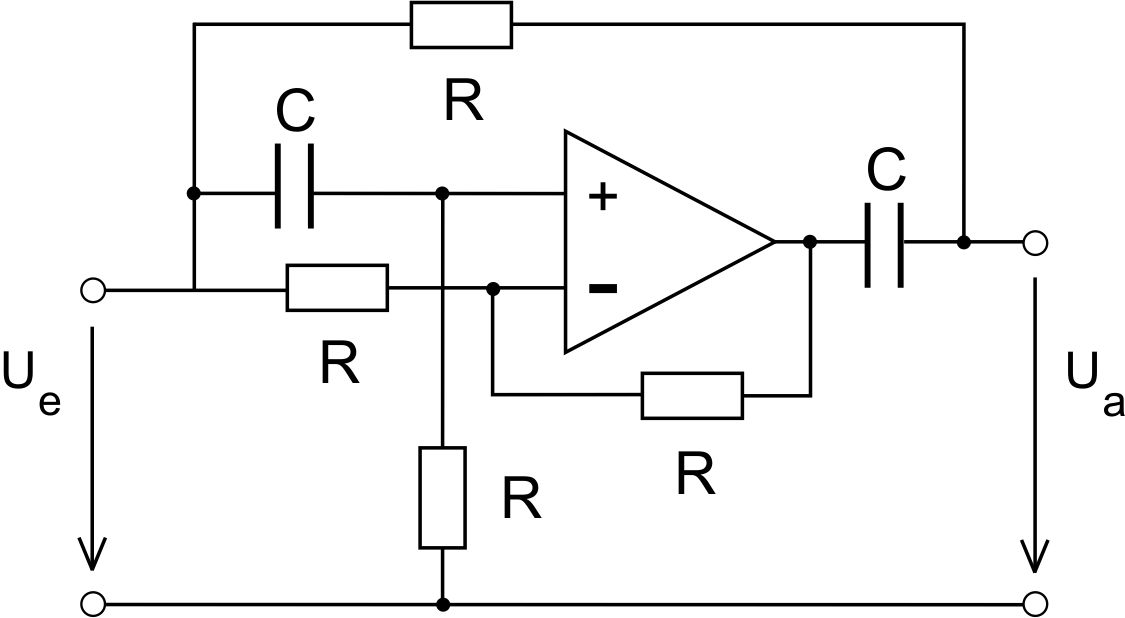
Ordnungen

Bandsperren höherer Ordnung können durch Verkettung einzelner Hoch- und Tiefpässe relisiert werden.

Übersicht

Bei den Filtern, die in der Tabelle aufgeführt sind,handelt es sich um passive RC-Filter erster Ordnung mit Butterworth-Verhalten. Im Wesentlichen verhalten sich Filter höherer Ordnung wie in den Diagrammen. Der Unterschied liegt in der Steilheit und in der größeren Phasenverschiebung. Pro Filterstufe nimmt die Phasenverschiebung um 90° zu.

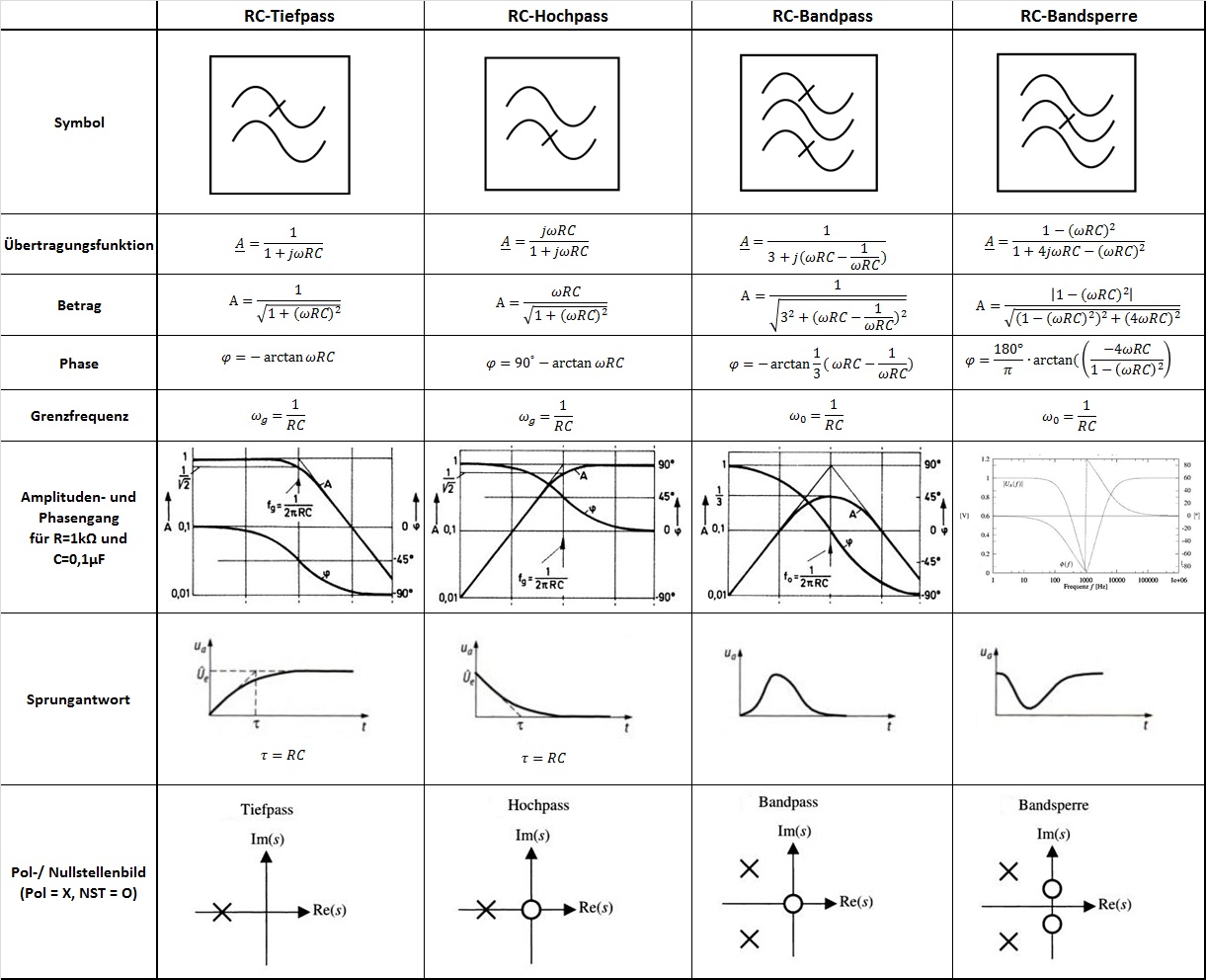
Charakteristische Größen [Bearbeiten]

Übertragungsfunktion

Filter können häufig als lineares, zeitinvariantes System beschrieben werden (siehe Abbildung 2.1).

Abb. 2.1: Blockschaltbild eines Systems

Falls für den Filterentwurf nur passive Strukturen verwendet werden, bleibt das Filter immer stabil. Damit lautet der Zusammenhang zwischen Ein- und Ausgangssignal

$$ y(t)=\int_{-\infty}^{\infty}h(\tau)x(t-\tau)\text{d}\tau $$

mit $$ h(t) $$ als der Impulsantwort, die bei Anregung mit dem Einheitsimpuls $$ \delta(t) $$ auftritt. Im Frequenzbereich erhält man mit

$$ Y(\text{j}\omega)=H(\text{j}\omega)X(\text{j}\omega) $$

die Übertragungsfunktion $$ H(\text{j}\omega) $$ des Systems. Diese können aufgeteilt werden in

$$ A(\text{j}\omega) :=\left| H(\text{j}\omega) \right| \, \text{(Amplitudengang)} $$

$$ \phi(\text{j}\omega) := \text{arg}( H(\text{j}\omega)) \, \text{(Phasengang)} $$

Für niedrige Frequenzen wird die Übertragungsfunktion häufig auf Basis von Strömen und Spannungen definiert. In vielen Fällen wird sie als das Verhältnis von Ausgangs- zu Eingangsspannung eines Zweitors verstanden. In der Hochfrequenztechnik müssen jedoch auch Reflexionen berücksichtigt werden. Daher wird die Übertragungsfunktion auf Basis von Wellengrößen festgelegt. Die folgende Abbildung 2.2 zeigt den allgemeinen Aufbau einer Schaltung mit Wellengrößen.

Abb. 2.2: Schaltung mit Wellenquelle, Zweitor und abschließender Last

Eine Quelle speist ein Zweitor, dessen Übertragungsfunktion gesucht wird. Die Schaltung ist mit einer Last abgeschlossen. Das Zusammenspiel der Wellengrößen wird im Signalflussgraphen (Abbildung 2.3) deutlich.

Abb. 2.3: Signalflussgraph der Schaltung

Neben den Streuparametern des Zweitors sind insbesondere der Reflexionsfaktor der Quelle $$ \Gamma_{G} $$ und der Reflexionsfaktor der Last $$ \Gamma_{L} $$ wichtige Parameter. Die Übertragungsfunktion des Zweitors ist definiert als das Verhältnis der aus dem Zweitor herausfließenden Welle $$ b_2 $$ und der Urwelle $$ b_G $$ der Quelle.

$$ H(\text{j}\omega) = \displaystyle\frac{b_2}{b_G}= \displaystyle\frac{s_{21}}{1-s_{11}\Gamma_G-s_{22}\Gamma_L+s_{11}s_{22}\Gamma_G\Gamma_L-s_{12}s_{21}\Gamma_G\Gamma_L} $$

Diese Definition wird verallgemeinerte Betriebs-Übertragungsfunktion oder Transducer-Übertragungsfunktion genannt. Ein besonderer Speziallfall tritt ein, wenn Quelle an das Zweitor optimal angepasst ist, sodass die Reflexion mit $$ \Gamma_G=0 $$ an der Quelle verschwindet.

$$ H(\text{j}\omega)|_{\Gamma_G=0} = \displaystyle\frac{s_{21}}{1-s_{22}\Gamma_L} $$

Falls nun auch Zweitor und Last reflexionsfrei angepasst sind, wird die Übetragungsfunktion besonders einfach.

$$ H(\text{j}\omega)|_{\Gamma_G,\Gamma_L=0} = s_{21} $$

Einfügungsdämpfung

Für die Spezifikation eines Filters wird häufig der Leistungsverlust durch das Filter im Durchlassbereich angegeben. Der Einfügungsgewinn ist zunächst definiert als das Verhältnis zweier Leistungen.

$$ G_E = \displaystyle\frac{P_t}{P_d} % = \frac{|b_2|^2-|a_2|^2}{|b_0|^2-|a_0|^2} $$

Dabei stellt $$ P_t $$ die tatsächlich in die Last abgegebene Wirkleistung dar.

Abb. 2.4: Schaltung mit Ersatzquelle zur Bestimmung von $$ P_t $$

Die Wirkleistung $$ P_d $$ stellt dagegen die Leistung dar, welche die Quelle unmittelbar in die Last abgibt. In diesem Fall existiert das Zweitor gar nicht und die Quelle ist mit der Last direkt verschaltet.

Abb. 2.5: Schaltung zur Bestimmung von $$ P_d $$

Setzt man die bekannten Größen zusammen mit den Streuparametern des Zweitors ein, so kann für den Einfügungsgewinn dann letztlich

$$ G_E = \displaystyle\frac{|s_{21}|^2 \left| 1-\Gamma_G\Gamma_L \right|^2}{\left| 1-s_{11}\Gamma_G-s_{22}\Gamma_L+s_{11}s_{22}\Gamma_G\Gamma_L-s_{12}s_{21}\Gamma_G\Gamma_L\right|^2} $$

geschrieben werden. Diese Definition ist jedoch mit Vorsicht zu behandeln. Falls $$ \Gamma_G $$ und $$ \Gamma_L $$ unterschiedliche Vorzeichen haben, kann selbst bei passiven Zweitoren eine Verstärkung auftreten. Daher sollte die Einfügungsdämpfung nur für reflexionsfrei angepasste Zweitore gemessen werden. Falls nun sowohl Quelle und Zweitor als auch Last und Zweitor reflexionsfrei angepasst sind, lautet die Einfügungsdämpfung (engl. insertion loss)

$$ A_E|_\text{dB} = -G_E|_{\text{dB}} = -20\log_{10}(|s_{21}|). $$

Phasenlaufzeit

Alle physikalischen Realisierungen von Filtern haben gemein, dass sie kausale Systeme sind. Reaktive Bauteile wie Kondensatoren, Induktivitäten und Leitungen bewirken immer mindestens eine zeitliche Verzögerung der Signale. Für die Beschreibung dieser Verzögerung gibt es die Größe der Phasenlaufzeit. Es wird zunächst angenommen, dass das Filter als Zweitor reflexionsfrei an Quelle und Last angepasst ist. Das Zweitor überträgt das Signal verzerrungsfrei. Es wird lediglich eine zeitliche Verzögerung und eine Dämpfung hervorgerufen. Damit gilt für hineinlaufende Welle $$ a_1 $$ und hinauslaufende Welle $$ b_2 $$

$$ b_2(t)=Ka_1(t-\tau_p). $$

Im Frequenzbereich lautet der Ausdruck

$$ b_2(\text{j}\omega)=Ka_1(\text{j}\omega)e^{-\text{j}\omega\tau_p}. $$

Daraus kann die Übertragungsfunktion

$$ H(\text{j}\omega)=\displaystyle\frac{b_2(\text{j}\omega)}{a_1(\text{j}\omega)}=K e^{-\text{j}\omega\tau_p} $$

entnommen werden. An der Übertragungsfunktion kann abgelesen werden, ob das Zweitor ein Signal verzerrungsfrei überträgt. Dazu muss der Betragsverlauf über alle Frequenzen konstant bleiben und die Phase darf sich nur linear über der Frequenz verändern.

$$ \left| H(\text{j}\omega) \right| = \text{const} $$

$$ \text{arg}( H(\text{j}\omega)) = -\omega\tau_p $$

Daraus ergibt sich die Phasenlaufzeit zu

$$ \tau_p = -\displaystyle\frac{\text{arg}( H(\text{j}\omega))}{\omega}, $$

die auch allgemein für beliebige Übertragungsfunktionen existiert. Allerdings behält diese Größe nur dann die Bedeutung einer Laufzeit, wenn der Betrag der Übertragungsfunktion über alle Frequenzen auch wirklich konstant bleibt.

Gruppenlaufzeit

Häufig reicht es aus, wenn das Filter ein verzerrungsfreies Verhalten nur über einem bestimmten Teil des Spektrums erfüllt. Die restriktiven Vorgaben für ein verzerrungfreies System aus der Definition der Phasenlaufzeit können durchaus gelockert werden, da in der Praxis bei einem Filter die Verzerrungsfreiheit ohnehin nur für den Durchlassbereich gefordert ist. Interessiert nur ein Frequenzband mit Mittenfrequenz $$ \omega_T $$, unterer Grenzfrequenz $$ \omega_{ug}=\omega_T - N\Delta\omega $$ und oberer Grenzfrequenz $$ \omega_{og}=\omega_T + N\Delta\omega $$, so gelten die neuen Bedingungen

$$ \left| H(\text{j}\omega) \right| = \text{const} & \qquad & \text{für} \quad 0<\omega_{ug}<|\omega|<\omega_{og} $$

$$ \text{arg}( H(\text{j}\omega)) = -\omega\tau_G+\chi & \qquad & \text{für} \quad 0<\omega_{ug}<|\omega|<\omega_{og} $$

Der Betrag der Übertragungsfunktion muss demnach nur innerhalb des Bandes konstant bleiben. Der Phasenverlauf darf jetzt auch eine additive Konstante $$ \chi $$ enthalten. Diese Konstante kann über einen Spezialfall festgelegt werden: Wird die Übertragungsfunktion lediglich an der Trägerschwingung $$ \omega_T $$ ausgewertet, so soll das System dort auch wirklich optimal verzerrungsfrei wirken.

$$ \text{arg}( H(\text{j}\omega_T)) = -\omega_T\tau_G+\chi \overset{!}{=} -\omega_T\tau_p $$

Damit gilt für die Konstante

$$ \chi = \omega_T(\tau_G-\tau_p). $$

Die Bedingungen für eine verzerrungsfreie Übertragung innerhalb eines Bandes lauten dann

$$ \left| H(\text{j}\omega) \right| = K = \text{const} \quad & \text{für} & \quad 0 <\omega_{ug}< |\omega|< \omega_{og} $$

$$ \text{arg}( H(\text{j}\omega)) = -\omega\tau_G+\omega_T(\tau_G-\tau_p) \quad & \text{für} & \quad 0 < \omega_{ug} < \omega < \omega_{og} $$

$$ \text{arg}( H(\text{j}\omega)) & = -\omega\tau_G-\omega_T(\tau_G-\tau_p) \quad & \text{für} & \quad -\omega_{og} < \omega < -\omega_{ug} $$

Die Größe $$ \tau_G $$ heißt Gruppenlaufzeit. Die Bedeutung als Laufzeit wird deutlich, wenn die Übertragungsfunktion auf ein Bandpasssignal angewandt wird. Ein Bandpasssignal enthält nur in einem endlichen Frequenzband spektrale Komponenten. Es kann als eine Summe periodischer Signale modelliert werden, deren Schwingfrequenzen um eine Trägerfrequenz $$ f_T=\omega_T/2\pi $$ zentriert sind (siehe Abbildung 2.6).

Abb. 2.6: Bandpasssignal im Frequenzbereich

Ein Bandpasssignal kann in der Form

$$ a_1(t)=\cos(\omega_T t+\phi)r(t) $$

ausgedrückt werden, wobei $$ r(t) $$ stellvertretend steht für eine Summe von harmonischen Schwingungen. Damit kann auch die Fouriertransformierte der einlaufenden Welle bestimmt werden.

$$ a_1(\text{j}\omega)=\frac{1}{2}R(\text{j}(\omega-\omega_T))e^{\text{j}\phi} + \frac{1}{2}R(\text{j}(\omega+\omega_T))e^{-\text{j}\phi} $$

Betrachtet man nur positive Frequenzen, so besitzt $$ a_1(\text{j}\omega) $$ ausschließlich spektrale Komponenten im Bereich $$ \left[ \omega_T - N\Delta\omega, \quad \omega_T + N\Delta\omega\right] $$. Es kann angenommen werden, dass das Filter alle spektalen Komponenten außerhalb von $$ [\omega_{ug}, \omega_{og}] $$ vollständig unterdrückt.

$$ b_2(\text{j}\omega) = H(\text{j}\omega) a_1(\text{j}\omega) = H(\text{j}\omega) \left[ \frac{1}{2}R(\text{j}(\omega-\omega_T))e^{\text{j}\phi} + \frac{1}{2}R(\text{j}(\omega+\omega_T))e^{-\text{j}\phi} \right] $$

$$ b_2(\text{j}\omega) = \frac{K}{2} e^{-\text{j}\omega\tau_G} \left[ R(\text{j}(\omega-\omega_T)) e^{\text{j}\omega_T(\tau_G-\tau_p)} e^{\text{j}\phi} + R(\text{j}(\omega+\omega_T)) e^{-\text{j}\omega_T(\tau_G-\tau_p)} e^{-\text{j}\phi} \right] $$

Das dazugehörige Zeitsignal lautet

$$ b_2(t) = K\cdot r(t-\tau_G)\cos\left(\omega_T(t-\tau_p)+\phi\right) $$

Es ist erkennbar, dass der informationstragende Teil $$ r(t) $$ mit der Gruppenlaufzeit $$ \tau_G $$ verzögert wird, das Trägersignal hingegen mit der Phasenlaufzeit $$ \tau_p $$. In Abbildung 2.7 wird ein Beispiel dargestellt. Eine Zweiseitenband-AM wird durch ein verzerrungsfreies Filter geschickt.

Abb. 2.7: Darstellung des Eingangssignals $$ x(t) $$ als Zweiseitenband-AM und des Ausgangssignals $$ y(t) $$ nach der Filterung durch ein verzerrungsfreies Filter.

Häufig wird die Gruppenlaufzeit auch über die Ableitung des Phasengangs nach der Frequenz definiert.

$$ \tau_G = -\displaystyle\frac{d\phi(\omega)}{d\omega} $$

Diese Definition gilt für beliebige Übertragungsfunktionen. Allerdings kann die Größe nur als Laufzeit interpretiert werden, wenn sowohl $$ \tau_G $$ als auch die Dämpfung im betrachteten Frequenzband konstant sind. Im allgemeinen Fall dient sie lediglich als Maß für die Verzerrungen, die ein Signal erfährt, wenn es durch das Filter gelangt.

Literatur

1. G. Zimmer, "Hochfrequenztechnik Lineare Modelle" , Springer-Verlag, 2000
2. A. Fettweis, "Elemente nachrichtentechnischer Systeme", J. Schlembach Fachverlag, 2004
3. M. H. W. Hoffmann, "Hochfrequenztechnik: Ein systemtheoretischer Zugang", Springer- Verlag, 1997
4. C. Roppel, "Grundlagen der digitalen Kommunikationstechnik", Hanser
   
5. K. Schmidt-Walter, "Taschenbuch der Elektrotechnik", Verlag Harri Deutsch
   
6. U. Tietze Ch. Schenk, "Halbleiter-Schaltungstechnik", Springer-Verlag 2002
   
7. E. Böhmer u.a, "Elemente der angewandten Elektronik", Vieweg + Teubner, Wiesbaden 2010
   
8. Internetseite: http://www.elektroniktutor.de/analog/filter.html