Wiki.inG

1 Einleitung
[Bearbeiten]

Bei Messungen mit Netzwerkanalysatoren (NWA) treten systematische Messfehler auf. Diese sind unter anderem bedingt durch Ungenauigkeiten der Bauteile des NWA und durch die Verbindungen vom NWA zum Messobjekt (Leitungen, Stecker, etc.).
Zur Korrektur dieser Messfehler muss ein NWA vor einer Messung kalibriert werden. Im Rahmen der Kalibrierung werden die Messfehler modellhaft vom Messobjekt getrennt, d.h. der zu messende Aufbau wird in drei Mehrtore aufgeteilt:

• ein Eingangs-Fehlerviertor $$ K $$ (lässt sich in ein Zweitor $$ R $$ überführen)
• das Messobjekt als Zweitor $$ S $$
• ein Ausgangs-Fehlerzweitor $$ T $$
  

Somit entsteht eine Reihenschaltung aus drei Zweitoren.

Abb. 1: Zweitordarstellung für die Messung mit einem Netzwerkanalysator

Die Größen $$ m_\mathrm{f} $$, $$ m_\mathrm{r} $$ und $$ m_\mathrm{t} $$ entsprechen den tatsächlich gemessenen Werten, die proportional zu den zulaufenden, reflektierten und transmittierten Wellen sind. Sie enthalten somit auch die Messfehler, die mittels der Fehlerzweitore beschrieben werden.

Anhand dieses Bildes ist zu erkennen, dass das Eingangs-Fehlerzweitor die Fehler der Referenz-Messung und der Messung der reflektierten Welle widerspiegelt. Die Fehler, die bei der Messung der transmittierten Wellen auftreten, werden durch das Ausgangs-Fehlerzweitor repräsentiert.

Durch geeignete Verfahren lassen sich vor der Messung die Matrix-Elemente von $$ R $$ und $$ T $$ bestimmen, wodurch eine fehlerbereinigte Messung ermöglicht wird. Dazu werden verschiedene Kalibrierstandards, deren Eigenschaften genau bekannt sein müssen, an die Messstellen des NWAs angeschlossen:

• angepasster Abschlusswiderstand
• Kurzschluss
• Leerlauf
• Durchverbindung

Mit den dabei gemessenen Werten lassen sich die Matrix-Elemente bestimmen.

2 Systemfehlerkorrektur mittels 3-Term-Verfahren [Bearbeiten]

Das 3-Term-Verfahren dient dazu einen NWA mit 2 Messstellen, also ein Reflektometer, zu kalibrieren. Dafür betrachten wir zuerst nur eine einfache Reflektometerschaltung, bei der das Messobjekt reflexionsfrei abgeschlossen ist (Abb. 2).

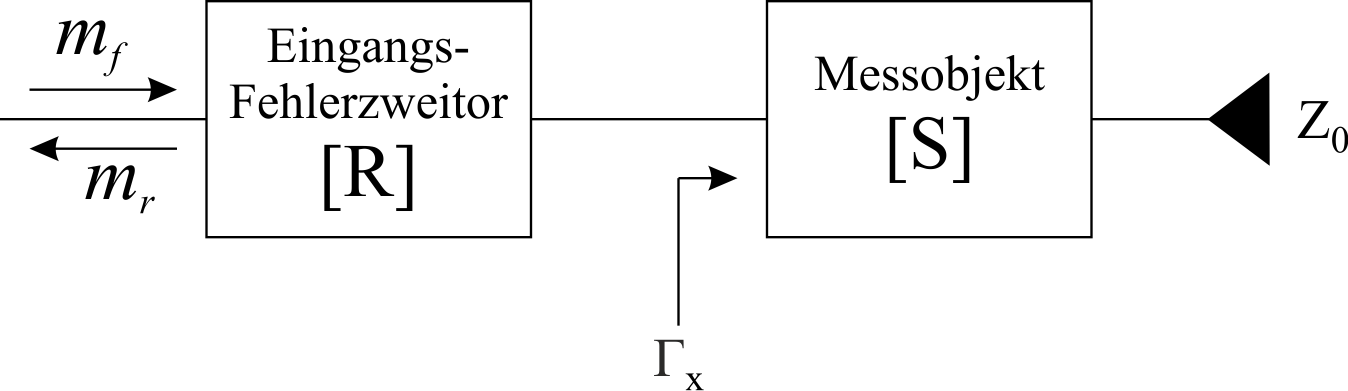
Abb. 2: Fehlertor beim 3-Term-Verfahren

Somit entfällt das Fehlerzweitor $$ T $$ und alle für diese Messung relevanten Fehler sind im Fehlerzweitor $$ R $$ zusammengefasst. Das von der Quelle ausgesendete Messsignal wird durch die Messgröße $$ m_\mathrm{f} $$ und das von der Kettenschaltung aus Fehlerzweitor $$ R $$ und Messobjekt $$ S $$ reflektierte Signal durch die Messgröße $$ m_\mathrm{r} $$ repräsentiert. Um nun die Reflexion des Messobjektes von Systemfehlern befreit zu bestimmen, muss das Fehlerzweitor bekannt sein, sodass von den gemessenen Größen $$ m_\mathrm{f} $$ und $$ m_\mathrm{r} $$ auf die gesuchte Reflexion $$ \Gamma_\mathrm{x} $$ des Messobjektes geschlossen werden kann. Zur Bestimmung der gemessenen Reflexion $$ \mu_\mathrm{x} = \frac{m_\mathrm{r}}{m_\mathrm{f}} $$ am Eingang der Kettenschaltung ist der entsprechende Signalflussgraph (SFG) in Abbildung 2 zu betrachten.

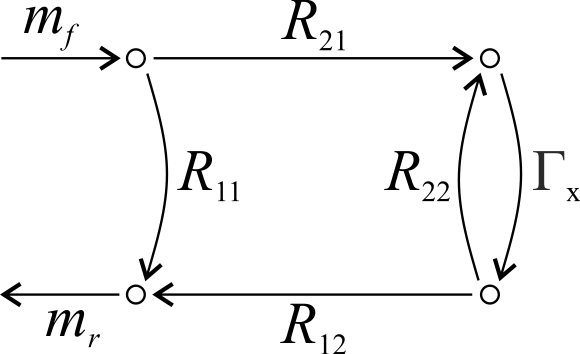
Abb. 3: Signalflussgraph beim 3-Term-Verfahren

Zur Herleitung einer analytischen Beschreibung der gemessenen Reflexion $$ \mu_\mathrm{x} $$ in Abhängigkeit der Matrixelemente des Fehlerzweitores $$ R $$ und der gesuchten Reflexion $$ \Gamma_\mathrm{x} $$ gibt es mehrere Ansätze. Beispielsweise kann der Zusammenhang direkt aus dem SFG abgeleitet werden. Hierfür muss zunächst die Schleife in dem SFG aufgelöst werden. Im Zuge dessen, soll anfags ein vereinfachter SFG, in Abbildung 4 zu sehen, betrachtet werden.

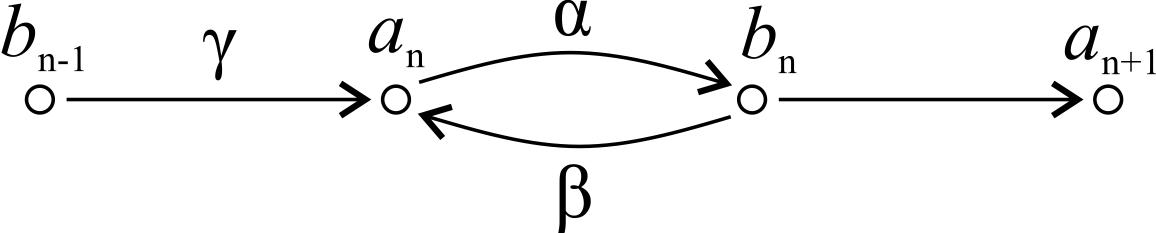
Abb. 4: Schleife in einem Signalflussgraph

Es gilt für den Knotenpunkt $$ a_\mathrm{n} $$:

$$ a_\mathrm{n} = \gamma b_\mathrm{n-1} + \beta b_\mathrm{n} = \gamma b_\mathrm{n-1} + \beta \alpha a_\mathrm{n} $$ (1)

$$ a_\mathrm{n} = \gamma b_\mathrm{n-1} \left(\frac{1}{1-\beta\alpha}\right) $$ (2)

So kann die Schleife folgendermaßen ersetzt werden (Abb. 5):

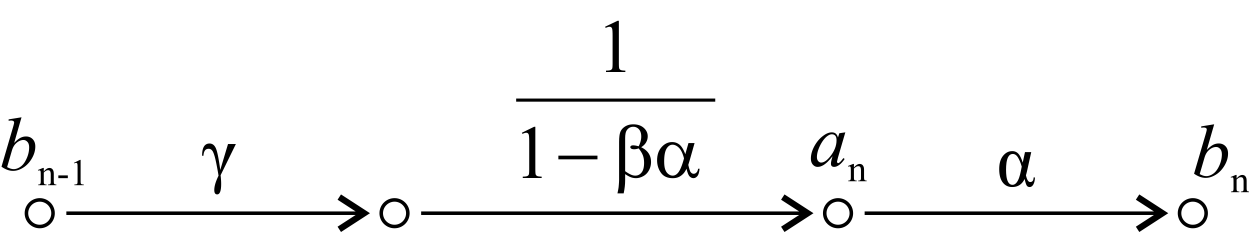
Abb. 5: Aufgelöste Schleife in einem Signalflussgraph

Für die zuvor betrachtete Kettenschaltung ergibt sich somit der in Abbildung 6a dargestellte SFG:

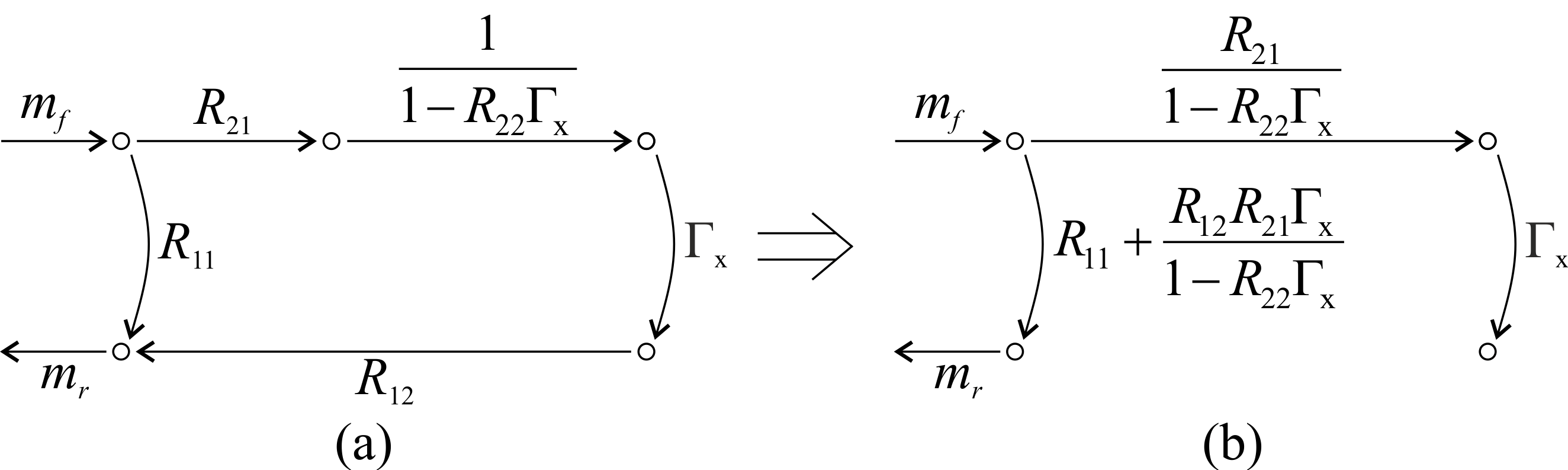
Abb. 6: Signalflussgraph beim 3-Term-Verfahren ohne Schleife

Aus dem weiter umgeformten SFG (Abb. 6b), kann die gemessene Reflexion einfach abgelesen werden:

$$ \mu_\mathrm{x} = \frac{m_\mathrm{r}}{m_\mathrm{f}} = R_\mathrm{11} + \frac{R_\mathrm{12} R_\mathrm{21} \cdot \Gamma_\mathrm{x}}{1 - R_\mathrm{22} \cdot \Gamma_\mathrm{x}} $$ (3)

Alternativ kann dieser Zusammenhang natürlich auch über die Streumatrix des Fehlerzweitors $$ R $$ hergeleitet werden, indem die Eingangs- und Ausgangswellengrößen entsprechend gewählt werden ( $$ a_1=m_\mathrm{f};~b_1=m_\mathrm{r};~a_2=\Gamma_\mathrm{x}b_2 $$ ). Dies kann je nach Umfang und Komplexität des SFG jedoch mehr Zeit in Anspruch nehmen.

Da die beiden Elemente $$ R_\mathrm{12} $$ und $$ R_\mathrm{21} $$ nur gemeinsam als Produkt auftauchen, können diese zu einem Fehlerterm zusammengefasst werden. Somit ergeben sich insgesamt drei Fehlerterme, welche im Rahmen der Kalibrierung bestimmt werden müssen:

$$ R_\mathrm{11} = ~? $$

$$ R_\mathrm{22} = ~? $$

$$ R_\mathrm{12} R_\mathrm{21} = ~? $$

Die Anzahl der unbekannten Fehlerterme sind übrigens Namensgeber dieses 3-Term-Verfahrens und folgender Kalibrierverfahren. Um diese drei Fehlerterme zu bestimmen sind drei Gleichungen nötig, welche man jeweils durch Messungen von insgesamt drei vollständig bekannten Kalibrierstandards erhält (Abb. 7).

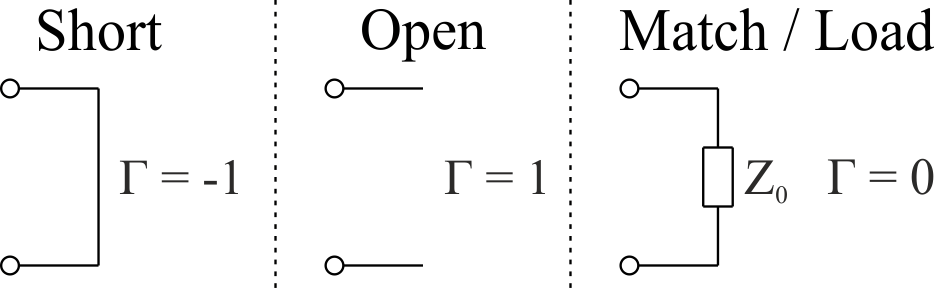
Abb. 7: Drei vollständig bekannte Kalibrierstandards

Dazu wird als Messobjekt zunächst ein Abschlusswiderstand vom Wert $$ Z_\mathrm{0} $$ verwendet, sodass das Fehlerzweitor $$ R $$ vollständig reflexionsfrei abgeschlossen ist. Durch diesen ideal angepassten Abschluss, welcher auch als Match (M) oder Load (L) bezeichnet wird, ergibt sich für den Reflexionsfaktor des Messobjektes $$ \Gamma_\mathrm{M} = 0 $$. Der erste Fehlerterm kann somit direkt bestimmt werden:

$$ \mu_\mathrm{M} = \frac{m_\mathrm{r,M}}{m_\mathrm{f,M}} = R_\mathrm{11} + \frac{R_\mathrm{12} R_\mathrm{21} \cdot 0}{1 - R_\mathrm{22} \cdot 0} = R_\mathrm{11} $$ (4)

Als zweiter Kalibrierstandard wird das Messobjekt durch einen Kurzschluss (Short, S) am Ausgang des Fehlerzweitors $$ R $$ ersetzt. Der Reflexionsfaktor ergibt sich so zu $$ \Gamma_\mathrm{S} = -1 $$, was in (3) eingesetzt die zweite Gleichung für die Bestimmung der Fehlerterme ergibt:

$$ \mu_\mathrm{S} = \frac{m_\mathrm{r,S}}{m_\mathrm{f,S}} = R_\mathrm{11} - \frac{R_\mathrm{12} R_\mathrm{21}}{1 - R_\mathrm{22}} $$ (5)

Zuletzt wird als dritter Kalibrierstandard ein Leerlauf (Open, $$ \Gamma_\mathrm{O} = 1 $$) am Ausgang des Fehlerzweitors $$ R $$ verwendet, was zu der Gleichung

$$ \mu_\mathrm{O} = \frac{m_\mathrm{r,O}}{m_\mathrm{f,O}} = R_\mathrm{11} + \frac{R_\mathrm{12} R_\mathrm{21}}{1 - R_\mathrm{22}} $$ (6)

führt. Zusammen mit Gleichung (5) und dem zuvor in Gleichung (4) bestimmten Fehlerterm $$ R_\mathrm{11} $$ lassen sich somit die verbleibenden Fehlerterme $$ R_\mathrm{22} $$ und $$ R_\mathrm{12} R_\mathrm{21} $$ bestimmen:

$$ R_\mathrm{11} = \mu_\mathrm{M} $$ (7)

$$ R_\mathrm{22} = \frac{2 R_\mathrm{11} - \mu_\mathrm{S} - \mu_\mathrm{O}}{\mu_\mathrm{S} - \mu_\mathrm{O}} $$ (8)

$$ R_\mathrm{12} R_\mathrm{21} = (\mu_\mathrm{O} - R_\mathrm{11}) \cdot (1 - R_\mathrm{22}) $$ (9)

Sind nach erfolgreicher Kalibrierung alle Fehlerterme nach oben genannten Gleichungen bestimmt, lässt sich der fehlerkorrigierte Reflexionsfaktor $$ \Gamma_\mathrm{x} $$ beliebiger Messobjekte durch Umstellen von Gleichung (3) bestimmen:

$$ \Gamma_\mathrm{x} = \frac{\mu_\mathrm{x} - R_\mathrm{11}}{R_\mathrm{12} \cdot \mu_\mathrm{x} + R_\mathrm{12} R_\mathrm{21} - R_\mathrm{11} R_\mathrm{22}} $$ (10)

3 Systemfehlerkorrektur mittels 5-Term-Verfahren [Bearbeiten]

Das 5-Term-Verfahren wird genutzt, um Netzwerkanalysatoren mit 3 Messstellen zu kalibrieren. Wie in Abbildung 8 zu sehen, wird diese weitere Messstelle dazu genutzt um ergänzend zur Reflexion zusätzlich die Transmission eines Messobjektes bestimmen zu können.

Abb. 8: Fehlertore beim 5-Term-Verfahren

Dadurch erhält man auch ein zweites Fehlerzweitor $$ T $$ zwischen dem Ausgang des Messobjektes und der dritten Messstelle. Um die Fehlerterme dieses Fehlerzweitors zu bestimmen, wird ein weiterer Kalibrierstandard benötigt, welcher jedoch im Unterschied zu den zuvor im 3-Term-Verfahren verwendeten Standards eine bekannte Transmission aufweisen muss, um so die Verbindung zwischen dem Messsignal und der weiteren Messstelle herzustellen. Für diesen Kalibrierstandard wird demnach eine ideale, angepasste Durchverbindung verwendet, welche auch als Through- (T-) Standard bezeichnet wird. Setzt man also eine Durchverbindung an der Stelle des Messobjektes ein und misst sowohl die Reflexion als auch die Transmission, ergeben sich im Hinblick auf den Signalflussgraphen (Abb. 9) zwei weitere Gleichungen:

Abb. 9: Signalflussgraph beim 5-Term-Verfahren bei einer Durchverbindung anstatt dem Messobjekt

$$ \mu_\mathrm{T,refl.} = \frac{m_\mathrm{r}}{m_\mathrm{f}} = R_\mathrm{11} + \frac{R_\mathrm{12} R_\mathrm{21} \cdot T_\mathrm{11}}{1 - R_\mathrm{22} \cdot T_\mathrm{11}} $$ (11)

$$ \mu_\mathrm{T,trans.} = \frac{m_\mathrm{t}}{m_\mathrm{f}} = \frac{R_\mathrm{21} \cdot T_\mathrm{21}}{1 - R_\mathrm{22} \cdot T_\mathrm{11}} $$ (12)

Es ist dabei zu beachten, dass für eine Systemfehlerkorrektur nach dem 5-Term-Verfahren, für die in das Fehlertor $$ T $$ einfallende Welle $$ a_\mathrm{t} = 0 $$ angenommen wird.

Zusammen mit den zuvor im 3-Term-Verfahren ermittelten Fehlertermen $$ R_\mathrm{11} $$, $$ R_\mathrm{22} $$ sowie $$ R_\mathrm{12} R_\mathrm{21} $$ enthalten die Gleichungen (11) und (12) zwei weitere zu bestimmende Fehlerterme $$ T_\mathrm{11} $$ sowie $$ R_\mathrm{21} T_\mathrm{21} $$.

Durch Umstellen der Gleichung (11) nach $$ T_\mathrm{11} $$ und anschließendem Einsetzen in Gleichung (12) und Auflösen nach $$ R_\mathrm{21} T_\mathrm{21} $$ ergeben sich die beiden noch verbleibenden Fehlerterme zu:

$$ T_\mathrm{11} = \left( \frac{R_\mathrm{12}R_\mathrm{21}}{\mu_\mathrm{T,refl.}-R_\mathrm{11}} + R_\mathrm{22} \right)^{-1} $$ (13)

$$ R_\mathrm{21}T_\mathrm{21} = (1-R_\mathrm{22}T_\mathrm{11}) \cdot \mu_\mathrm{T,trans.} $$ (14)

Sind im Rahmen der Kalibrierung nun alle 5 Fehlerterme bestimmt, muss nach der zunächst fehlerbehafteten Messung eines unbekannten Zweitors mit Hilfe der Fehlerterme auf die korrigierten Streuparameter dieses Zweitors zurückgerechnet werden. Dazu wird zunächst die Kettenschaltung aus Abbildung 8, bestehend aus Fehlerzweitor $$ R $$, Messobjekt $$ S $$ sowie Fehlerzweitor $$ T $$ , zu einem Gesamtzweitor $$ W $$ zusammengefasst, da sich auf dieses Zweitor die in der Messung bestimmten Größen $$ m_\mathrm{f} $$, $$ m_\mathrm{r} $$ sowie $$ m_\mathrm{t} $$ beziehen. Damit ergeben sich mit den gemessenen Größen die Zusammenhänge:

$$ W_\mathrm{11} = \frac{m_\mathrm{r}}{m_\mathrm{f}} $$ (15)

und

$$ W_\mathrm{21} = \frac{m_\mathrm{t}}{m_\mathrm{f}} $$ (16)

Da in dieser Konfiguration das Messobjekt nur an Tor 1 angeregt wird, ist es nur möglich die Reflexion am Eingangstor und die Transmission in Vorwärtsrichtung zu bestimmen. Um das Messobjekt vollständig zu charakterisieren und damit alle S-Parameter zu bestimmen, muss eine zweite Messung durchgeführt werden, bei der Eingang und Ausgang des Messobjektes vertauscht werden. Somit können auch die Reflexion am anderen Tor und die Transmission in umgekehrter Richtung bestimmt werden. Das für diesen Fall resultierende Gesamtzweitor, bestehend aus Fehlerzweitor $$ R $$, Messobjekt $$ S $$ für den Fall, dass Eingang und Ausgang vertauscht sind sowie Fehlerzweitor $$ T $$, wird mit $$ X $$ bezeichnet. Somit gilt:

$$ X_\mathrm{11} = \frac{m_\mathrm{r}}{m_\mathrm{f}} $$ (17)

$$ X_\mathrm{21} = \frac{m_\mathrm{t}}{m_\mathrm{f}} $$ (18)

Betrachtet man für die Zweitore $$ W $$ und $$ X $$ jeweils die Transmissionsmatrizen, ist ersichtlich, dass jeweils der zweite Spaltenvektor durch die Messung bekannt ist:

$$ \begin{pmatrix} \frac{-\Delta W}{W_\mathrm{21}} & \frac{W_\mathrm{11}}{W_\mathrm{21}} \\ -\frac{W_\mathrm{22}}{W_\mathrm{21}} & \frac{1}{W_\mathrm{21}} \end{pmatrix} $$ (19)
und
$$ \begin{pmatrix} \frac{-\Delta X}{X_\mathrm{21}} & \frac{X_\mathrm{11}}{X_\mathrm{21}} \\ -\frac{X_\mathrm{22}}{X_\mathrm{21}} & \frac{1}{X_\mathrm{21}} \end{pmatrix} $$ (20)

Stellt man nun die Gleichungen gemäß der Kettenschaltung in Abbildung 8 in Transmissionsmatrixdarstellung auf und betrachtet davon ebenfalls nur die rechten Spatenvektoren, erhält man folgende Gleichungen:

$$ \begin{bmatrix} \frac{W_\mathrm{11}}{W_\mathrm{21}} \\ \frac{1}{W_\mathrm{21}} \end{bmatrix} = \frac{1}{R_\mathrm{21} T_\mathrm{21}} \begin{bmatrix} -\Delta R & R_\mathrm{11} \\ -R_\mathrm{22} & 1 \end{bmatrix} \cdot \frac{1}{S_\mathrm{21}} \begin{bmatrix} -\Delta S & S_\mathrm{11} \\ -S_\mathrm{22} & 1 \end{bmatrix} \cdot \begin{bmatrix} T_\mathrm{11} \\ 1 \end{bmatrix} $$ (21)

$$ \begin{bmatrix} \frac{X_\mathrm{11}}{X_\mathrm{21}} \\ \frac{1}{X_\mathrm{21}} \end{bmatrix} = \frac{1}{R_\mathrm{21} T_\mathrm{21}} \begin{bmatrix} -\Delta R & R_\mathrm{11} \\ -R_\mathrm{22} & 1 \end{bmatrix} \cdot \frac{1}{S_\mathrm{21}} \begin{bmatrix} -\Delta S & S_\mathrm{22} \\ -S_\mathrm{11} & 1 \end{bmatrix} \cdot \begin{bmatrix} T_\mathrm{11} \\ 1 \end{bmatrix} $$ (22)

Dabei ist zu beachten, dass in Gleichung (22) $$ S_\mathrm{11} $$ und $$ S_\mathrm{22} $$ vertauscht sind, was mit der Vertauschung von Eingang und Ausgang des Messobjektes bei der zweiten Messung zu begründen ist. Durch die Messungen des unbekannten Messobjektes sind die linken Seiten der Gleichungen vollständig bekannt. Ebenso sind auf der rechten Seite alle Terme links und rechts der Transmissionsmatrixdarstellung von $$ S $$ bekannt. Multipliziert man nun die Gleichungen (21) und (22) jeweils von links mit dem Ausdruck

$$ \left( \frac{1}{R_\mathrm{21} T_\mathrm{21}} \begin{bmatrix} -\Delta R & R_\mathrm{11} \\ -R_\mathrm{22} & 1 \end{bmatrix} \right)^{-1} $$

ergeben sich die beiden stark vereinfachten Gleichungen

$$ \begin{bmatrix} y_\mathrm{1} \\ y_\mathrm{2} \end{bmatrix} = \frac{1}{S_\mathrm{21}} \begin{bmatrix} -\Delta S & S_\mathrm{11} \\ -S_\mathrm{22} & 1 \end{bmatrix} \cdot \begin{bmatrix} T_\mathrm{11} \\ 1 \end{bmatrix} $$ (23)

und

$$ \begin{bmatrix} y_\mathrm{3} \\ y_\mathrm{4} \end{bmatrix} = \frac{1}{S_\mathrm{21}} \begin{bmatrix} -\Delta S & S_\mathrm{22} \\ -S_\mathrm{11} & 1 \end{bmatrix} \cdot \begin{bmatrix} T_\mathrm{11} \\ 1 \end{bmatrix} $$ (24)

mit

$$ \frac{1}{R_\mathrm{21} T_\mathrm{21}} \begin{bmatrix} -\Delta R & R_\mathrm{11} \\ -R_\mathrm{22} & 1 \end{bmatrix} \cdot \begin{bmatrix} \frac{W_\mathrm{11}}{W_\mathrm{21}} \\ \frac{1}{W_\mathrm{21}} \end{bmatrix} = \begin{bmatrix} y_\mathrm{1} \\ y_\mathrm{2} \end{bmatrix} $$ (25)

$$ \frac{1}{R_\mathrm{21} T_\mathrm{21}} \begin{bmatrix} -\Delta R & R_\mathrm{11} \\ -R_\mathrm{22} & 1 \end{bmatrix} \cdot \begin{bmatrix} \frac{X_\mathrm{11}}{X_\mathrm{21}} \\ \frac{1}{X_\mathrm{21}} \end{bmatrix} = \begin{bmatrix} y_\mathrm{3} \\ y_\mathrm{4} \end{bmatrix} $$ (26)

Demzufolge sind $$ y_\mathrm{1} $$, $$ y_\mathrm{2} $$, $$ y_\mathrm{3} $$ und $$ y_\mathrm{4} $$ vollständig aus den Messungen sowie der Kalibrierung bekannt. Die vier Gleichungen, welche in den Gleichungen (23) und (24) enthalten sind, bilden ein Gleichungssystem, mit dem $$ S_\mathrm{11} $$, $$ S_\mathrm{12} $$, $$ S_\mathrm{21} $$ sowie $$ S_\mathrm{22} $$ bestimmt werden können:

$$ S_\mathrm{11} = \frac{y_\mathrm{1} y_\mathrm{4} - T_\mathrm{11}}{y_\mathrm{2} y_\mathrm{4} - T_\mathrm{11}^2} $$ (27)

$$ S_\mathrm{22} = \frac{y_\mathrm{2} y_\mathrm{3} - T_\mathrm{11}}{y_\mathrm{2} y_\mathrm{4} - T_\mathrm{11}^2} $$ (28)

$$ S_\mathrm{12} = \frac{1 - T_\mathrm{11} S_\mathrm{11}}{y_\mathrm{4}} $$ (29)

$$ S_\mathrm{21} = \frac{1 - T_\mathrm{11} S_\mathrm{22}}{y_\mathrm{2}} $$ (30)

Damit ist das zu vermessende Zweitor $$ S $$ vollständig bekannt. Die gesamte Rechnung gilt jedoch nur für einen einzelnen Frequenzpunkt, daher muss die komplette Kalibrierung sowie Rechnung bis hin zu den korrigierten S-Parametern für jeden Frequenzpunkt einzeln durchgeführt werden, was in einem Netzwerkanalysator im Rampenbetrieb automatisch erfolgt.

4 Systemfehlerkorrektur mittels 10-Term-Verfahren [Bearbeiten]

Da beim 5-Term-Verfahren das Messobjekt von der Messung in Vorwärtsrichtung für die in Rückwärtsrichtung manuell gedreht werden muss, erweist sich dieses Vorgehen häufig als unpraktisch und fehleranfällig, denn die Verbindungen zum Messobjekt müssen manuell gelöst und wieder verbunden werden und sind unter Umständen nicht exakt reproduzierbar. Daher ist es weitaus besser, durch einen hochfrequenztauglichen Umschalter im Messgerät das Messobjekt automatisch an beiden Toren hintereinander anzuregen, sodass ein manuelles Lösen der Verbindungen und Umdrehen des Messobjektes vermieden wird (Abb. 10). Bei diesem Messverfahren wird zur Kalibrierung im Prinzip nur das 5-Term-Verfahren zweimal hintereinander, einmal für jede Schalterstellung, angewendet, was zu insgesamt 10 Fehlertermen führt. Dabei übernimmt in der zweiten Schalterstellung einfach das Fehlerzweitor $$ T $$ die Rolle des Fehlerzweitors $$ R $$ in Schalterstellung 1 und umgekehrt. Die gesamte Rechnung bleibt identisch wie beim 5-Term-Verfahren und dient daher ebenfalls zur Kalibrierung eines NWAs mit 3 Messstellen.

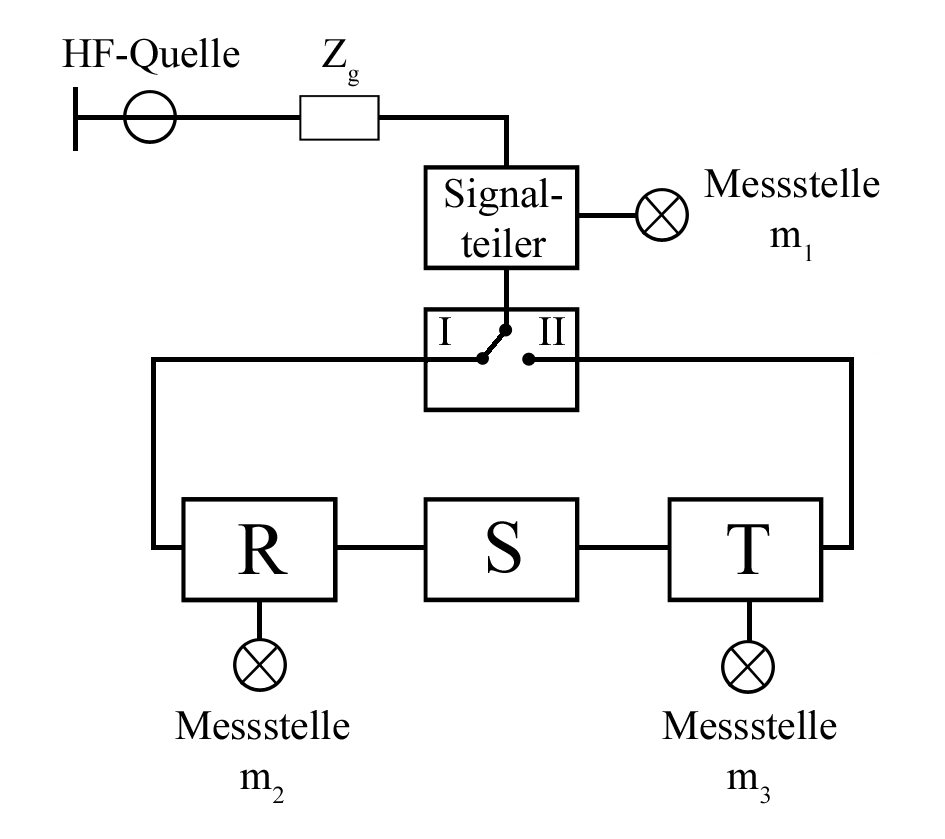
Abb. 10: Netzwerkanalysator mit 3 Messstellen und Schalter

Nichtidealitäten des Schalters, wie beispielsweise eine Dämpfung, werden dabei durch die Kalibrierung kompensiert. Dennoch ergeben sich gewisse Anforderungen an den Schalter. Dieser muss zum einen eine sehr gute Reproduzierbarkeit der einzelnen Schalterstellungen aufweisen und es dürfen keine Übersprecher in Schalterstellung 1 auf Schalterstellung 2 und umgekehrt stattfinden, da bei der Kalibrierung für die am nicht angeregten Tor einfallende Welle $$ a_\mathrm{t} = 0 $$ angenommen wurde (Abb. 9). Übersprecher des Schalters im Rahmen einer Kalibrierung zu berücksichtigen ist nur bei einem Netzwerkanalysator mit 4 Messstellen möglich. Dieser hat eine weitere Messstelle für hinlaufende Wellen an Tor 2, wodurch andere Kalibrierverfahren möglich sind.

5 Literaturverzeichnis
[Bearbeiten]

1. B. Schiek, "Grundlagen der Hochfrequenztechnik", Springer, 1999