Radargleichung

Die Radargleichung ist eine der grundlegensten Gleichungen zur Beschreibung von Radarsystemen. Sie ermöglicht die Bestimmung der maximalen Reichweite eines Radarsystems bzw. das für eine gewünschte Reichweite benötigte Verhältnis von Sendeleistung zu minimal detektierbarer Leistung am Empfänger in Abhängigkeit von den Eigenschaften der verwendeten Antenne, der Frequenz, den Reflexionseigenschaften des zu detektierenden Objektes sowie dem Ausbreitungsmedium, in dem das System betrieben wird. Ebenso lässt sich mit Hilfe der Radargleichung abschätzen, ob bei einem vorhandenen Radarsystem ein gegebenes Ziel in bekanntem Abstand ein ausreichend stark reflektiertes Signal am Empfänger erzeugt.

Da die für die Reflexion von elektromagnetischen Wellen relevanten Eigenschaften eines Radarziels u.a. stark von der Größe eines Objektes abhängen, unterscheidet man grundsätzlich zwischen zwei verschiedenen Varianten der Radargleichung. Für elektrisch kleine Streukörper, deren Reflexion wiederum als Punktquelle angesehen werden kann, ergibt sich somit eine andere Radargleichung als für elektrisch große Volumenziele. Die Unterscheidung zwischen elektrisch großen und elektrisch kleinen Objekten erfolgt anhand der verwendeten Wellenlänge des Radarsystems:

$$ \lambda = \frac{c}{f} $$ (1)

Für Ziele deren Abmessungen sich im Bereich der Wellenlänge $$ \lambda $$ oder darunter befinden spricht man von elektrisch kleinen Zielen. Andersherum werden Objekte, deren Abmessungen deutlich größer als $$ \lambda $$ sind, als elektrisch große Objekte bezeichnet, sodass für solche Ziele eine andere Variante der Radargleichung zum Einsatz kommt. Nachfolgend sollen nun beide Varianten der Radargleichung ausführlich erklärt und hergeleitet werden.

Grundlagen zum Abstrahlverhalten von Antennen

Um den Zusammenhang von Sende- und Empfangsleistung herzuleiten, wird zunächst von einem isotropen Kugelstrahler als Sender ausgegangen, welcher die Leistung $$ P_{\mathrm S} $$ abstrahlt. Da die Leistung in alle Richtungen gleichmäßig abgestrahlt wird, ergeben sich konzentrisch um den Strahler Kugelschalen gleicher Leistungsdichte, welche mit zunehmenden Abstand $$ R $$ vom Zentrum des Senders auf Grund der Strahldivergenz geringer wird (Abb. 1):

$$ S_{\mathrm i} = \frac{P_{\mathrm S}}{4 \cdot \pi \cdot R^2} $$. (2)

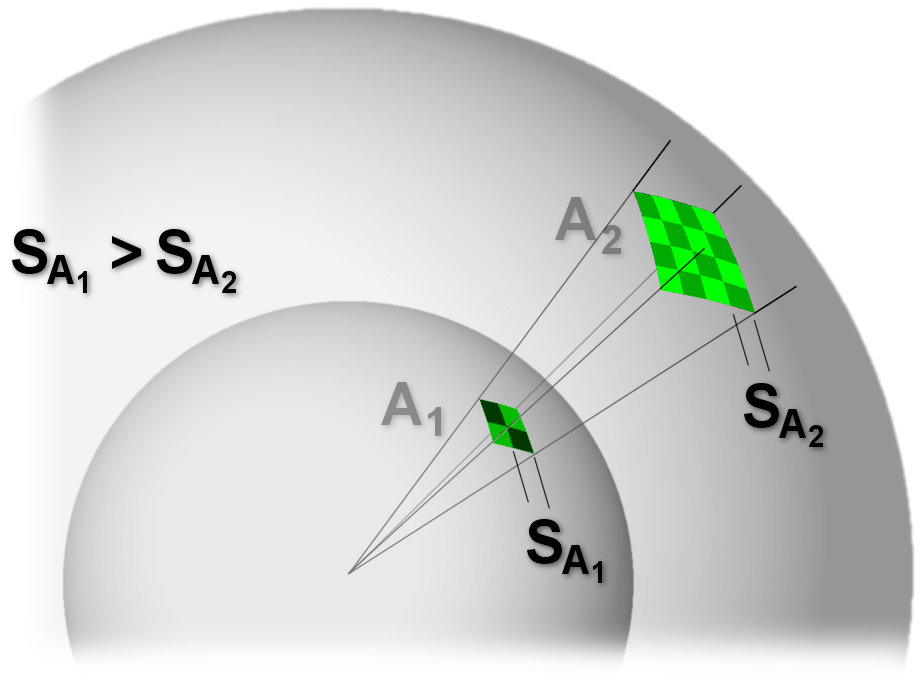
Abb. 1: Strahldivergenz beim isotropen Kugelstrahler [1]

Antennen, welche für Radaranwendungen verwendet werden, strahlen die eingespeiste Leistung in der Regel nicht in alle Raumrichtungen ab, sondern bündeln diese und formen so einen i.d.R. möglichst scharf begrenzten Strahl welcher einen sehr geringen Strahlquerschnitt aufweist und oft als Hauptkeule der Antenne bezeichnet wird. Da die von der Antenne abgestrahlte Leistung so auf einen bedeutend kleineren Raumwinkel konzentriert wird, fällt die gerichtete Leistungsdichte innerhalb dieses Raumwinkels deutlich größer aus. Diese Verstärkung der Leistungsdichte im Vergleich zu einem isotropen Kugelstrahler wird mit Hilfe des Antennengewinns $$ G $$ beschrieben. In Abb. 2 ist beispielsweise ein Richtdiagramm einer Antenne mit hoher Richtwirkung angegeben.

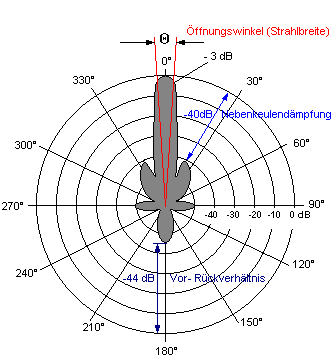
Abb. 2: Richtdiagramm einer Antenne [2]

Es ist deutlich die Hauptabstrahlrichtung bei $$ \Theta = 0^\circ $$ zu erkennen, in welche die Leistung hautsächlich abgetrahlt wird. Der Faktor, um welchen die Leistungsdichte in der Hauptabstrahlrichtung der Antenne größer ist als die eines isotropen Kugelstrahlers wird als Antennengewinn $$ G $$ bezeichnet. Die von einer Antenne abgestrahlte Leistungsdichte ergibt sich so zu:

$$ S_{\mathrm A} = S_{\mathrm i} \cdot G $$. (3)

Radargleichung für elektrisch kleine Streukörper

Wie viel Leistung von einem Streukörper reflektiert wird, hängt in erster Linie vom Radarquerschnitt $$ \sigma $$ ab, welcher abhängig von der Größe, Form und Beschaffenheit des Objektes ist. Zusammen mit dem Radarquerschnitt ergibt sich die vom Ziel reflektierte Leistung zu:

$$ P_{\mathrm R} = S_{\mathrm A} \cdot \sigma = \frac{P_{\mathrm S}}{4 \cdot \pi \cdot R^2} \cdot G \cdot \sigma $$. (4)

Für elektrisch kleine Ziele wird die refklektierte Leistung in alle Richtungen zurück gestreut, womit die Reflexion am Objekt wieder als Kugelwelle bzw. als Punktstrahler betrachtet werden kann. Somit kann die Leistungsdichte am Empfänger auf dem gleichen Wege berechnet werden, wie bei einem isotropen Kugelstrahler:

$$ S_{\mathrm E} = \frac{P_{\mathrm R}}{4 \cdot \pi \cdot R^2} $$. (5)

Die Leistung, welche eine Antenne einem vorhandenem Feld, welches durch eine Strahlungsdichte gegeben ist, entnehmen kann, ist abhängig von ihrer Apertur sowie der Apertureffizienz. Die Apertur einer Antenne bezeichnet die Größe bzw. geometrische Fläche einer Antenne. Bei einer Parabolantenne entspricht die Aptertur beispielsweise der Reflektorgröße, bei einer Hornantenne der Größe der Öffnung des Hornes. Da jedoch nicht die gesamte Fläche der Antenne dem Feld Leistung entnehmen kann, beschreibt die Aptertureffizienz den Anteil der Fläche, welcher dem Feld effektiv Leistung entnimmt und am Ausgang der Antenne zur Verfügung stellt. Diese Apertureffizienz ist maßgeblich abhängig von der verwendeten Wellenlänge, sowie dem Gewinn und der Antennenfläche selber. Das Produkt von geometrischer Antennenfläche sowie der Apertureffizienz bezeichnet man als Antennenwirkfläche. Sie bezeichnet die elektrisch wirksame Fläche der Antenne und ist gegeben durch:

$$ A_{\mathrm W} = A_{\mathrm geo} \cdot \eta_{\mathrm eff} = \frac{\lambda^2}{4 \cdot \pi} \cdot G $$. (8)

Bei Antennentypen wie beispielsweise Linearantennen (Dipol, Monopol, etc.) wird zur Berechnung ebenfalls die Antennenwirkfläche verwendet, jedoch ist die Betrachtung über die geometrische Größe im Zusammenhang mit der Apertureffizienz eher unüblich. Hier wird die Antennenwirkfläche direkt als Funktion der Wellenlänge und des Gewinns betrachtet. Die Leistung, die eine Antenne nun dem Feld entnimmt und welche damit am Empfänger zur Verfügung steht, ist somit gegeben durch das Produkt der Leistungsdichte $$ S_{\mathrm E} $$ und der Antennenwirkfläche $$ A_{\mathrm W} $$:

$$ P_{\mathrm E} = S_{\mathrm E} \cdot A_{\mathrm W} $$ (7)

Fasst man nun die Gleichungen (4) bis (7) zusammen, erhält man für die gesamte empfangene Leistung:

$$ P_{\mathrm E} = \frac{P_{\mathrm S} \cdot G^2 \cdot \sigma \cdot \lambda^2}{\left( 4 \cdot \pi \right)^3 \cdot R^4} $$. (8)

Um neben der geometrischen Ausbreitung zusätzlich noch die Dämpfung durch das Ausbreitungsmedium (i.d.R. Luft) sowie geräteinterne Verluste zu berücksichtigen, wird Gleichung (8) um den Faktor $$ \frac{1}{L(f)} $$ erweitert, in welchem diese Verluste zusammengefasst sind:

$$ P_{\mathrm E} = \frac{P_{\mathrm S} \cdot G^2 \cdot \sigma \cdot \lambda^2}{\left( 4 \cdot \pi \right)^3 \cdot R^4} \cdot \frac{1}{L(f)} $$. (9)

Stellt man diese Gleichung nun nach dem Abstand $$ R $$ um, so ergibt sich:

$$ R = \left( \frac{P_{\mathrm S} \cdot G^2 \cdot \sigma \cdot \lambda^2}{\left( 4 \cdot \pi \right)^3 \cdot P_{\mathrm E}} \cdot \frac{1}{L(f)} \right)^\frac{1}{4} $$ (10)

was im Allgemeinen als Radargleichung bekannt ist. Setzt man anstelle der Empfangsleistung $$ P_{\mathrm E} $$ die minimal vom Empfänger detektierbare Leistung ein, erhält man die maximal zu detektierende Entfernung des Radarsystems.

Radargleichung für elektrisch große Volumenziele

Anders als bei elektrisch kleinen Streukörpern, kann die Reflexion an großen Volumenzielen nicht selbst wieder als Punktstrahler bzw. als Kugelwelle betrachtet werden. Nachfolgend soll am Beispiel einer unendlich großen Metallwand als Ziel (Abb. 3) die Radargleichung bzw. die Leistungsbilanz für den Fall elektrisch großer Volumenziele hergeleitet werden.

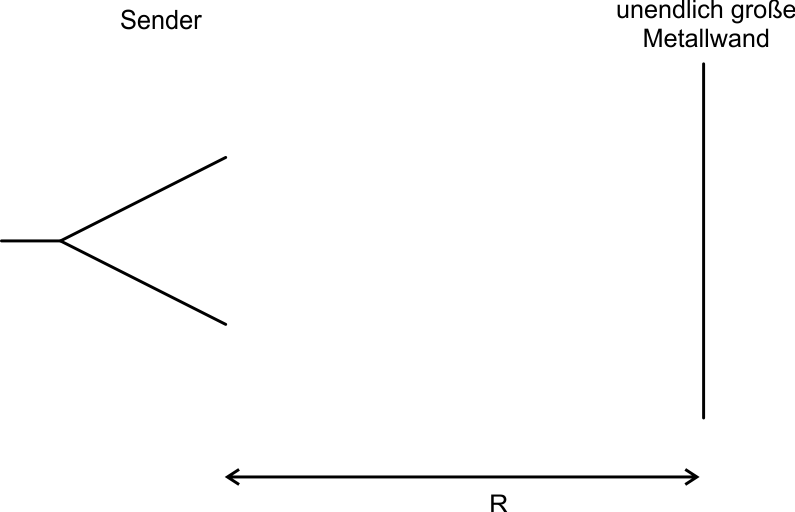
Abb. 3: Szenario für ein elektrisch großes Ziel

Wird als Ziel eine elektrisch leitfähige, unendlich große Metallwand betrachtet, so gelten an der Metallwand bestimmte Randbedingungen, welche erfüllt sein müssen. Dazu zählt, dass die Tangentialkomponente des elektrischen Feldes verschwinden muss ($$ \vec{E}_{\mathrm tan} = 0 $$) und somit die einfallende Welle gegenphasig reflektiert wird. Da die reflektierte Welle bis auf eine Phasendrehung von $$ \Delta \phi = 180^\circ $$ und der entgegengesetzten Ausbreitungsrichtung genau der einfallenden Welle entspricht, lässt sich für die Berechnung der am Empfänger ankommenden Leistung das Prinzip der Spiegelquelle ansetzen. Demnach kann anstelle der unendlich ausgedehnten Metallwand eine exakt gleiche Quelle in doppeltem Abstand angenommen werden, welche mit einer Phasenverschiebung von $$ \phi = 180^\circ $$ sendet (Abb. 4).

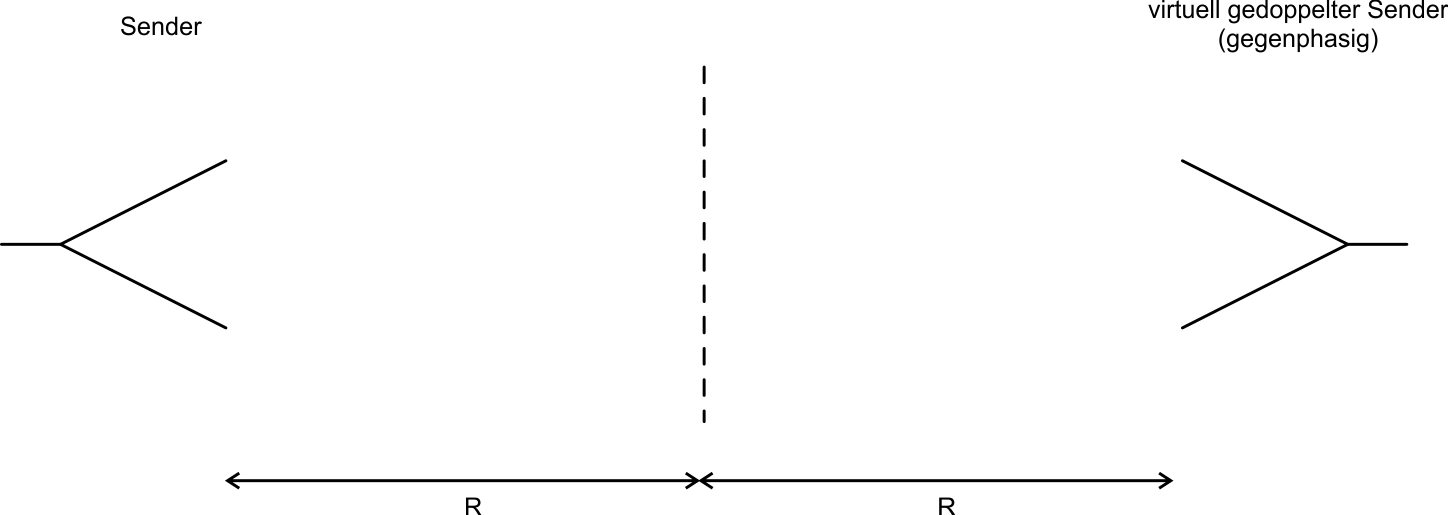
Durch die Wahl der genau doppelten Entfernung sowie der Phasenverschiebung um $$ \phi = 180^\circ $$ überlagern sich die Feldkomponenten des eigentlichen Senders und der Spiegelquelle im Abstand $$ R $$ zum ursprünglichen Sender destruktiv, sodass auch hier die Bedingung $$ \vec{E}_{\mathrm tan} = 0 $$ an der Stelle $$ R $$ gilt, womit wir in der Ebene der Metallwand einen virtuellen Kurzschluss erhalten und somit die Randbedingungen der Metallwand erfüllt sind.

Um nun die am Empfänger ankommende Leistungsdichte zu berechnen, muss lediglich die von der Spiegelquelle abgestrahlte Leistungsdichte in der Entfernung $$ 2 \cdot R $$ berechnet werden. Dies geschieht wieder durch die Betrachtung der Leistungsdichte eines isotropen Kugelstrahlers und der Multiplikation mit dem Antennengewinn:

$$ S_{\mathrm E} = \frac{P_{\mathrm S}}{4 \pi \cdot (2R)^2} \cdot G $$. (11)

Durch Multiplikation mit der Antennenwirkfläche ergibt sich die vom Empfänger detektierte Leistung:

$$ P_{\mathrm E} = S_{\mathrm E} \cdot A_{\mathrm W} = \frac{P_{\mathrm S} \cdot G \cdot A_{\mathrm W}}{16 \pi \cdot R^2} $$. (12)

Für eine vergleichbare Darstellung bzw. um die Berechnung der maximal detektierbaren Entfernung zu ermöglichen, ergibt sich für Gleichung (12) nach $$ R $$ umgestellt:

$$ R = \sqrt{\frac{P_{\mathrm S} \cdot G \cdot A_{\mathrm W}}{16 \pi \cdot P_{\mathrm E}}} $$. (13)

Schlussfolgerung

Bei Betrachtung der beiden Varianten der Radargleichung ist ersichtlich, dass die Größe eines Radarziels einen entscheidenen Einfluss auf die reflektierte Leistung hat. Somit fällt die am Empfänger detektierte Leistung für elektrisch kleine Ziele in Abhängigkeit von der Entfernung proportional zu $$ \frac{1}{R^4} $$ ab, wohingegen die Empfangsleistung für elektrisch große Ziele für größere Entfernungen lediglich mt $$ \frac{1}{R^2} $$ abfällt. Somit lassen sich bei Radarsystemen mit ansonsten identischen Eigenschaften und Kennwerten sowie unter Vernachlässigung der Freiraumdämpfung bei elektrisch großen Zielen höhere Reichweiten erzielen als bei elektrisch kleinen Zielen.

Literaturverzeichnis

[1]  http://de.wikipedia.org/wiki/Leistungsdichte

[2]  http://epzilon.org/facharbeit/sendeantenne.shtml