10.4a Rechenregeln für Grenzwerte (Fortsetzung)
10.4 Rechenregeln für Grenzwerte (Fortsetzung)
Grenzwerte und Anordnung
Eine wichtige Eigenschaft von Grenzwerten besteht darin, dass sie die Anordnung nicht ändern. Wenn das n-te Glied \(x_n\) einer Folge also immer kleiner oder gleich dem n-ten Glied \(y_n\) einer anderen Folge ist (und wenn beide Folgen einen Grenzwert besitzen), dann gilt diese Sortierung auch für die Grenzwerte.
\(x_n\leq y_n\;\) für alle \(\;n\in\mathbb{N}\)
erfüllt ist, dann ist auch\(\lim\limits_{n\to\infty}x_n\leq\lim\limits_{n\to\infty}y_n.\)
Beweisidee: Man argumentiert hier indirekt, das heißt, man zeigt, dass \(\lim\limits_{n\to\infty}x_n\leq\lim\limits_{n\to\infty}y_n\) sein muss, weil \(\lim\limits_{n\to\infty}x_n > \lim\limits_{n\to\infty}y_n\) nicht sein kann.
Wäre nämlich der Grenzwert \(\lim \limits _{n\to \infty } x_n\) größer als der Grenzwert \(\lim \limits _{n\to \infty } y_n\), dann könnte man ein Folgenglied \(x_N\) und ein Folgenglied \(y_ N\) mit einem sehr großen Index \(N\) finden, die beide schon sehr nahe an dem jeweiligen Grenzwert der Folge liegen. Die Folgenglieder und Grenzwerte würden also in etwa so auf der Zahlengeraden liegen:
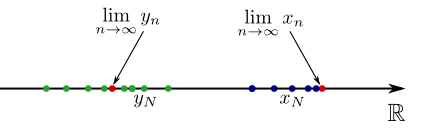
Das kann aber nicht sein, da dann die Vorausetzung \(x_ N \leq y_ N\) nicht erfüllt wäre. Damit kann auch \(\lim \limits _{n\to \infty } x_ n > \lim \limits _{n\to \infty } y_ n\) nicht wahr sein.
☐
Achtung! Es ist durchaus möglich, dass für alle \(n\in \mathbb{N}\) sogar die echte Ungleichung \(x_n < y_n\) gilt und trotzdem \(\lim \limits_{n\to \infty } x_n = \lim\limits_{n\to \infty } y_n \) ist.
Man kann diesen Satz benutzen, um die Konvergenz einer Folge zu beweisen, indem man sie zwischen zwei Folgen mit demselben Grenzwert "einzwängt":
\(x_n\leq y_n\leq z_n\;\) für alle \(\;n\in\mathbb{N}\)
genügen. Falls die Grenzwerte \(\lim\limits_{n\to\infty}x_n=\lim\limits_{n\to\infty}z_n\) existieren, dann konvergiert auch die Folge \((y_n)_{n\in \mathbb{N}}\) und es gilt\(\lim\limits_{n\to\infty}y_n=\lim\limits_{n\to\infty}x_n=\lim\limits_{n\to\infty}z_n\).
-
Es ist \(\lim \limits _{n\to \infty }\displaystyle\frac {n^2+\cos (3n)}{2n^2+3} = \displaystyle\frac{1}{2}\), denn da der Cosinus nur Werte zwischen \(-1\) und \(1\) annimmt ist
\(\displaystyle\frac{n^2-1}{2n^2+3}{\leq}\displaystyle\frac{n^2+\cos(3n)}{2n^2+3}{\leq}\displaystyle\frac{n^2+1}{2n^2+3}\).
Es ist aber
\(\lim\limits_{n\to\infty}\displaystyle\frac{n^2-1}{2n^2+3}=\lim\limits_{n\to\infty}\displaystyle\frac{1-\frac{1}{n^2}}{2+\frac{3}{n^2}}=\displaystyle\frac{1}{2}\)
und genauso \(\lim \limits _{n\to \infty }\displaystyle\frac {n^2+1}{2n^2+3}=\displaystyle\frac {1}{2}\). Daher ist die Folge \(\left(\displaystyle\frac {n^2+\cos (3n)}{2n^2+3} \right)\) trotz der Oszillationen des Cosinus zwischen zwei Folgen eingezwängt, die beide denselben Grenzwert haben. Also muss auch die Folge selbst gegen den Grenzwert \(\displaystyle\frac {1}{2}\) konvergieren.
-
Es gilt
\(\lim\limits_{n\to\infty}\displaystyle\frac{n!}{n^n}=0\)
denn
\(0\leq\displaystyle\frac{n!}{n^n}=\displaystyle\frac{1\cdot 2\cdot 3\cdot\ldots\cdot n}{n^n}\leq\displaystyle\frac{1}{n}\to 0.\)
-
Es ist \(\lim \limits _{n\to \infty }\sqrt [n]{2^ n+3^ n} = 3\), denn etwas Jonglieren mit Potenzgesetzen zeigt
\(3=\sqrt[n]{3^n} \leq \sqrt[n]{2^n+3^n}{\leq}\sqrt[n]{2 \cdot 3^n}=\sqrt[n]{2} \cdot \sqrt[n]{3^n}\)
Da
\(\lim\limits_{n\to\infty}\sqrt[n]{2}\sqrt[n]{3^n}=\lim\limits_{n\to\infty}\sqrt[n]{2}\cdot\lim\limits_{n\to\infty}\sqrt[n]{3^n}=1\cdot 3=3\)
ist die Folge \((\sqrt[n]{2^n+3^n})\) zwischen zwei Folgen "eingequetscht", die beide gegen \(3\) konvergieren. Damit muss sie ebenfalls gegen \(3\) konvergieren.
