11.5a Trigonometrische Funktionen (Fortsetzung)
11.5 Trigonometrische Funktionen (Fortsetzung)
Die Sinus- und Cosinusfunktion
Im Studium wird es auch wichtig sein, Sinus und Cosinus nicht nur als eine Beziehung zwischen geometrischen Objekten zu betrachten, sondern als Funktionen .
Mit den obigen Überlegungen am Einheitskreis kann man die Nullstellen des Sinus und des Cosinus bestimmen. Der Sinus als \(y\)-Koordinate eines Punktes auf dem Einheitskreis verschwindet genau dann, wenn der Winkel \(\varphi\) ein Vielfaches eines halben Umlaufs ist:
\(\sin(\varphi)=0\;\Leftrightarrow\;\varphi\in\{0,\pm\pi,\pm 2\pi,\pm 3\pi,\dots\}=\{k\pi;\;k\in\mathbb{Z}\}\)
Zusammen mit der Periodizität und den oben berechneten speziellen Werten kann man nun schon (fast) das Schaubild der Sinusfunktion zeichnen:

Beim Cosinus betrachtet man die \(x\)-Koordinate eines Punktes auf dem Einheitskreis. Diese ist genau dann Null, wenn der Winkel \(\varphi \) entweder \(\frac{\pi }{2}\) oder \(\frac{\pi }{2}\) plus ein Vielfaches eines halben Umlaufs ist:
\(\cos(\varphi)=0\;\Leftrightarrow\;\varphi\in\left\{\pm\frac{\pi}{2},\pm\frac{3\pi}{2},\pm\frac{5\pi}{2},\dots\right\}=\left\{\frac{\pi}{2}+k\pi;\;k\in\mathbb{Z}\right\}\)
Als Schaubild erhalten wir dann:
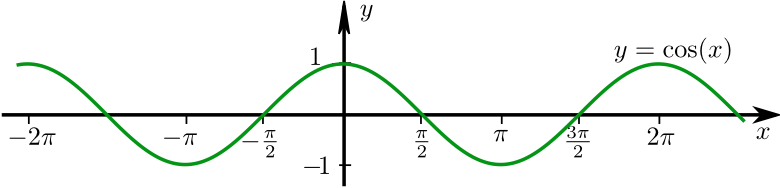
Das sieht genauso aus wie das Schaubild der Sinusfunktion, nur um etwas nach rechts (oder links, wie man möchte) verschoben. Um diese Beobachtung ganz streng zu verifizieren, benötigen wir die Additionstheoreme, mit denen man um eine festen Betrag \(\psi\) verschobene Sinusfunktionen \(\sin (\varphi +\psi )\) umformen kann.
Additionstheoreme für Sinus- und Cosinusfunktion
In Formelsammlungen finden sich viele Additionstheorem, Halbwinkelformeln, etc. für Sinus und Cosinus. Mit etwas Geschick kann man die allermeisten auf zwei grundlegende Additionsformeln zurückführen.
\(\begin{array}{rcl}\sin(\alpha+\beta)&=&\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta)\\& &\\\cos(\alpha+\beta)&=&\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)\end{array}\)
Einen rein geometrischer Beweis zumindest für den Fall, dass \(\alpha +\beta < \frac{\pi }{2}\) sind, enthält die folgende Graphik:
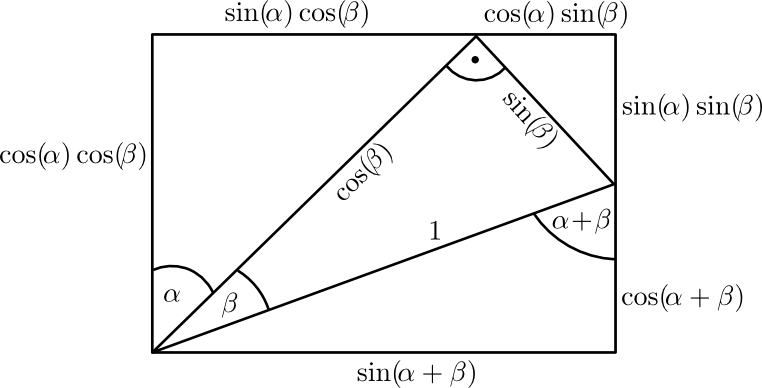
Aus diesen beiden Formeln lassen sich viele weitere trigonometrische Identitäten herleiten, z.B.
\( \begin{array}{rcl} \sin( 2\alpha)= \sin( \alpha+\alpha) & \stackrel{\mathbf{(1)}}{=}& 2\sin(\alpha) \cos(\alpha) \\ \cos( 2\alpha) = \cos( \alpha+\alpha) & \stackrel{\mathbf{(2)}}{=}& \cos^2(\alpha)- \sin^2(\alpha) \\ &&\\\sin( \alpha-\beta)= \sin( \alpha+(-\beta)) & \stackrel{\mathbf{(3)}}{=}& \sin(\alpha) \cos(-\beta) +\cos(\alpha) \sin(-\beta) \\ &\stackrel{\mathbf{(4)}}{=} & \sin (\alpha) \cos (\beta) -\cos (\alpha) \sin (\beta) \\ &&\\ \cos(\alpha-\beta)= \cos(\alpha+(-\beta)) & \stackrel{\mathbf{(5)}}{=} & \cos(\alpha) \cos(-\beta) - \sin(\alpha) \sin(-\beta) \\ & \stackrel{\mathbf{(6)}}{=} & \cos (\alpha) \cos (\beta) + \sin (\alpha) \sin(\beta) \\ &&\\ \sin(\alpha+\displaystyle\frac{\pi}{2}) & \stackrel{\mathbf{(7)}}{=} & \sin (\alpha) \cos(\frac{\pi}{2}) + \cos(\alpha) \sin(\frac{\pi}{2}) \stackrel{\mathbf{(8)}}{=} \cos (\alpha) \end{array} \)
Es ist eine gute Übung, sich bei allen Gleichheitszeichen in diesem Kasten noch einmal klarzumachen, warum sie gelten.
