11.5b Trigonometrische Funktionen (Fortsetzung)

11.5 Trigonometrische Funktionen (Fortsetzung)

Die Tangensfunktion

Auch für den Tangens wollen wir uns das Schaubild und die Additionstheoreme noch überlegen. Da \(\tan (\varphi ) =\displaystyle\frac {\sin (\varphi )}{\cos (\varphi )}\) sind die Nullstellen der Tangensfunktion genau dieselben wie bei der Sinusfunktion:

\(\tan(\varphi)=0\;\Leftrightarrow\;\varphi\in\{0,\pm\pi,\pm2\pi,\pm3\pi,\dots\}=\{k\pi;\;k\in\mathbb{Z}\}\)

Andererseits müssen alle Punkte aus dem Definitionsbereich ausgeschlossen werden, in denen \(\cos (\varphi)=0\) ist. Der Definitionsbereich der Tangensfunktion ist daher

\(D=\mathbb{R}\setminus\left\{\frac{\pi}{2}+k\pi;\;k\in\mathbb{Z}\right\}=\dots\cup\left(-\displaystyle\frac{3\pi}{2},-\displaystyle\frac{\pi}{2}\right)\cup\left(-\displaystyle\frac{\pi}{2},\displaystyle\frac{\pi}{2}\right)\cup\left(\displaystyle\frac{\pi}{2},\displaystyle\frac{3\pi}{2}\right)\cup\dots\)

und das Schaubild ist periodisch mit Periode \(\pi \):

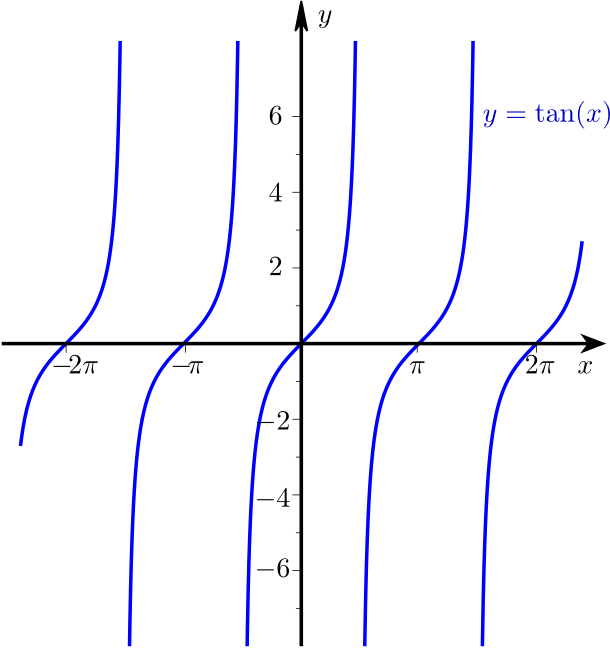
Die Additionstheorem für den Tangens lassen sich aus den Additionstheoremen für Sinus und Cosinus herleiten:

\( \begin{array}{rcl}
\tan(\alpha+\beta)=\displaystyle\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}
& =& \displaystyle\frac{\sin(\alpha) \cos(\beta) +\cos(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta) - \sin(\alpha) \sin(\beta)} \\
& & \\
&=&\displaystyle\frac{ \displaystyle\frac{\sin(\alpha) \cos(\beta)}{\cos(\alpha) \cos(\beta)} +\displaystyle\frac{\cos(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta)}\ }{ \displaystyle\frac{\cos(\alpha) \cos(\beta)}{\cos(\alpha) \cos(\beta)} - \displaystyle\frac{\sin(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta)}} \\
& & \\
& = & \displaystyle\frac{\tan(\alpha) + \tan(\beta)}{1 - \tan(\alpha) \tan(\beta)}
\end{array}\)

Auf dieselbe Weise erhält man

\(\tan(\alpha-\beta)=\displaystyle\frac{\tan(\alpha)-\tan(\beta)}{1+\tan(\alpha)\tan(\beta)}\)

und wenn man in der Formel für \(\tan (\alpha +\beta )\) speziell \(\alpha =\beta\) wählt,

\(\tan(2\alpha)=\displaystyle\frac{2\tan(\alpha)}{1-\tan^2(\alpha)}.\)