11.5c Trigonometrische Funktionen Fortsetzung
11.5 Trigonometrische Funktionen (Fortsetzung)
Inverse trigonometrische Funktionen
Weder die Sinus-, noch die Cosinus- noch Tangensfunktion sind bijektiv, d.h. Gleichungen wie
\(\sin( x)=0.5,\qquad\cos( y)=-\displaystyle\frac{\sqrt{2}}{2}\;\;\text{oder}\;\;\tan( w)=2025\)
haben keine eindeutige Lösung.
▸ Klicken, um Details anzuzeigen
Die Gleichung \(\sin(x) = 0,5 \) hat die Lösungen \( x = \frac{\pi}{6} \) und \( x = \frac{5\pi}{6} \) (und wegen der Periodizität der Sinusfunktion unendlich viele weitere Lösungen).
Die Gleichung \(\cos( y)=-\displaystyle\frac{\sqrt{2}}{2}\) hat die Lösungen \( y = \frac{3\pi}{4} \) und \( y = -\frac{3\pi}{4} \) (und wegen der Periodizität der Cosinusfunktion unendlich viele weitere Lösungen).
Trotzdem möchte man Umkehrfunktionen definieren, um zunächst wenigstens eine der Lösungen dieser Gleichungen zu finden (und damit dann mit etwas Nachdenken auch alle anderen).
Der Ausweg besteht darin, wie bei den Wurzelfunktionen vorzugehen und den Definitionsbereich geeignet einschzuränken.
-
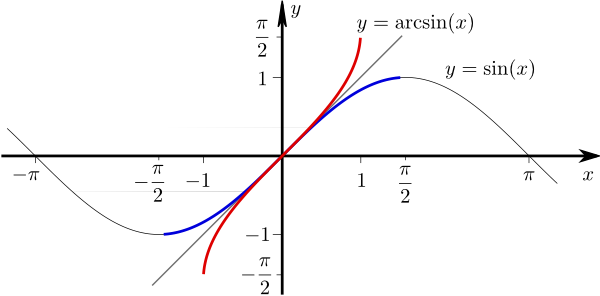
Schränkt man die Sinusfunktion auf das Intervall \(\left[ -\displaystyle\frac {\pi }{2}, \displaystyle\frac {\pi }{2}\right]\) ein (den im Schaubild unten blau markierten Bereich), so ist sie dort streng monoton wachsend und damit umkehrbar.
Ihre Umkehrfunktion ist auf dem Intervall \(\left[ -1, 1\right]\) definiert und heißt Arcussinus.
-
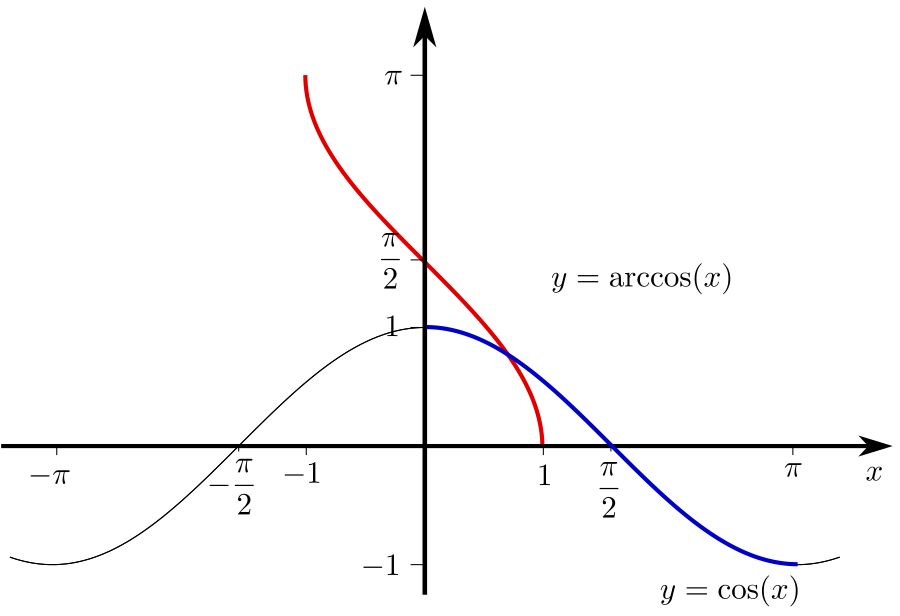
Schränkt man die Cosinusfunktion auf das Intervall \(\left[0,\pi \right]\) ein (den im Schaubild unten blau markierten Bereich), so ist sie streng monoton fallend und damit umkehrbar.
Ihre Umkehrfunktion ist auf dem Intervall \(\left[ -1, 1\right]\) definiert und heißt Arcuscosinus.
-
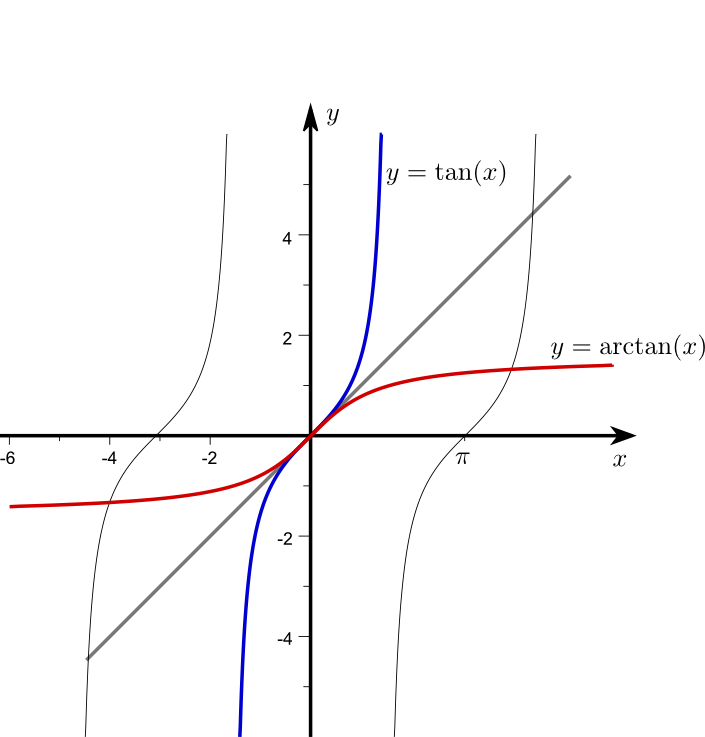
Schränkt man die Tangensfunktion auf das Intervall \(\left( -\displaystyle\frac {\pi }{2}, \displaystyle\frac {\pi }{2}\right)\) ein, so ist sie streng monoton wachsend und damit umkehrbar.
Ihre Umkehrfunktion ist auf ganz \(\mathbb {R}\) definiert und heißt Arcustangens.