15.3 Volumen und Mantelfläche von Rotationskörpern
15.3 Volumen und Mantelfläche von Rotationskörpern
Lässt man ein Kurve \(y=f(x)\) mit \(a \leq x\leq b\) im \(\mathbb{R}^3\) um die x-Achse rotieren, so entsteht ein Rotationskörper, dessen Volumen sich mit Hilfe (eindimensionaler!) Integration bestimmen lässt.
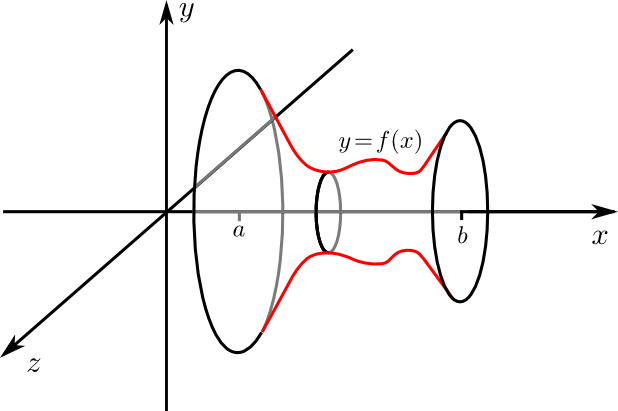
Das Volumen des Rotationskörper kann man annähern, indem man ihn in Scheiben zerlegt. Ist die Breite dieser Scheiben \(\Delta x\), so entspricht deren Radius ungefähr dem $y$-Wert, also dem Funktionswert \(f(x)\) und jede Scheibe hat damit ein Volumen \(\pi (\Delta x)f( x)^2\). Zerlegt man also das Intervall \([a,b]\) durch die Punkte \(x_ j=a+j\Delta x\) der Länge \(\Delta x=\frac{b-a}{n}\), dann erhält man als Näherungswert für das Volumen des Rotationskörpers die Summe
$V_n=\sum\limits_{j=1}^n\pi f(x_j)^2\cdot\Delta x$
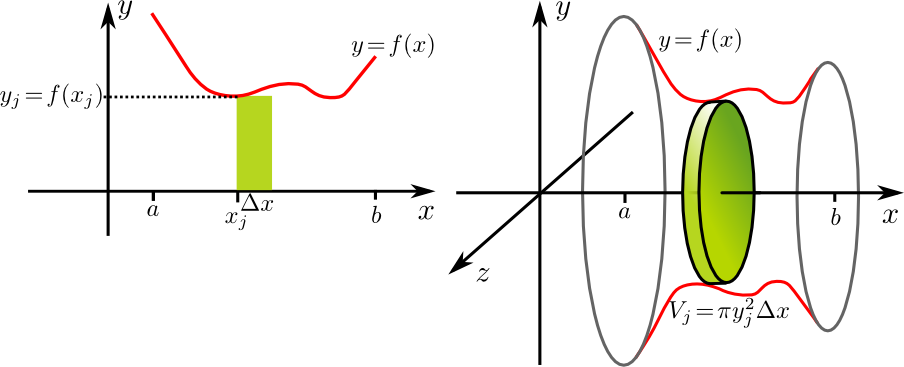
Geht man zu immer dünneren Scheiben über, so kommt man im Grenzfall \(\Delta x\to 0\) bzw. \(n\to \infty\) auf das Integral
\(V=\pi\displaystyle\int\limits_a^bf^2(x)\,\mathrm{d}x.\)
\(V=\pi\displaystyle\int\limits_a^b f^2(x)\,\mathrm{d}x\,.\)
Eine Kugel vom Radius \(R\) kann man als Rotationskörper erzeugen, indem man den Graph von \(f(x)=\sqrt {R^2-x^2}\) über dem Intervall \([-R,R]\) um die \(x\)-Achse rotieren lässt.
Ihr Volumen ist dann
\(V=\pi\displaystyle\int\limits_{-R}^R\left(\sqrt{R^2-x^2}\right)^2\,\mathrm{d}x=\pi\int\limits_{-R}^R\left(R^2-x^2\right)^2\,\mathrm{d}x=\left.\pi(R^2x-\dfrac{x^3}{3})\right|_{x=-R}^R=\dfrac{4}{3}\pi R^3.\)
Die Gewichtskraft einer sehr dünnen homogenen Scheibe konstanter Dicke, die um eine Achse drehbar ist, bewirkt ein Drehmoment. Es gibt einen ausgezeichneten Punkt, den Schwerpunkt \(S\), so dass dieses Drehmoment für jede Achse durch \(S\) verschwindet.
Wie lassen sich die Koordinaten von \(S\) bestimmen?
Sei dazu \(A\) die Fläche zwischen den Graphen von \(f_1\) und \(f_2\), also von der folgenden Form:
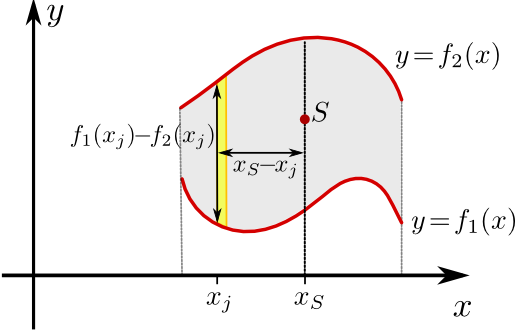
Bezüglich einer zur \(y\)-Achse parallele Drehachse ist das Drehmoment aller Massenelemente, die in einem zur \(y\)-Achse parallelen Streifen \(S_ j\) der Breite \(\Delta x\) fast gleich. Damit trägt dieser Streifen zum Gesamtdrehmoment den Anteil
\(M_j=g\mu\underbrace{(f_2(x_j)-f_1(x_j))\Delta x}_{=\text{Fläche des Streifens}}\cdot\underbrace{(x_S-x_j)}_{\text{Hebelarm}}\)
wobei \(g\) die Erdbeschleunigung und \(\mu\) die Massendichte bezogen auf die Fläche ist.
Durch Summation aller Momente und Übergang zu immer schmaleren Streifen, erhält man als Gesamtdrehmoment
\(M=g\mu\displaystyle\int\limits_a^b(f_2(x)-f_1(x))(x_S-x)\,\mathrm{d}x\,.\)
Gesucht ist derjenige Wert \(x_ S\), für den \(M=0\) ist. Durch einfache Umformungen erhält man
\(x_S=\frac{\int\limits_a^b(f_2(x)-f_1(x))x\,\mathrm{d}x}{\int\limits_a^b(f_2(x)-f_1(x))\,\mathrm{d}x}\,.\)
Da der Nenner gerade der Flächeninhalt
\(A=\displaystyle\int_a^b(f_2(x)-f_1(x))\,\mathrm{d}x\)
ist, kann man auch
\(x_S A=\displaystyle\int\limits_a^b(f_2(x)-f_1(x))x\,\mathrm{d}x\)
schreiben.
Liegt die Drehachse parallel zur \(x\)-Achse, dann sind die Streifen senkrecht zur Achse. Man erhält dann mit ähnlichen Überlegungen für die \(y\)-Koordinate des Schwerpunkts den Ausdruck
\(y_S A=\dfrac{1}{2}\displaystyle\int\limits_a^b(f_2^2(x)-f_1^2(x))\,\mathrm{d}x\,.\)
Vergleicht man diesen Ausdruck wiederum mit dem Volumen des Rotationskörpers, der entsteht, wenn man die Fläche um die \(x\)-Achse rotieren lässt, erhält man das folgende Resultat:
Mantelfläche von Rotationskörpern
Auch die Mantelfläche von Rotationskörpern kann man auf ähnliche Weise bestimmen. Hier genügt es nicht, den Rotationskörper durch Zylinder zu approximieren, sondern man muss das Stück zwischen \(x_ j\) und \(x_{j+1}\) durch einen Kegelstumpf mit den Radien \(f(x_ j)\) und \(f(x_{j+1})\) sowie der Höhe \(\Delta x=x_{j+1}-x_ j\) annähern. Daraus erhält man dann:
\(M=2\pi\displaystyle\int\limits_a^b f(x)\sqrt{1+f’(x)^2}\,\mathrm{d}x\,.\)
Evangelista Torricelli ( 1608 - 1647 ) war ein Schüler von Galilei und fand das folgende Beispiel, das unter dem Namen Torricellis Trompete oder Gabriels Horn bekannt ist, sehr irritierend. Er betrachtete die (unendlich ausgedehnte) Kurve \(y=\frac{1}{x}\) mit \(1\leq x < \infty\), die um die \(x\)-Achse rotierend einen Körper erzeugt, der dem Schallbecher einer Trompete ähnelt.
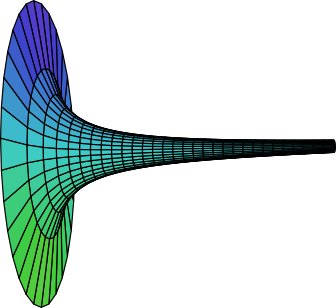
Das Volumen kann man durch einen Grenzübergang bestimmen. Zunächst ist für denjenigen Teil der Trompete mit \(1\leq x \leq R\) nach unserer Formel für das Volumen von Rotationskörpern
\(V(R)=\pi\displaystyle\int\limits_1^R\dfrac{\mathrm{d}x}{x^2}=\left.-\dfrac{\pi}{x}\right|_{x=1}^R=\pi-\dfrac{\pi}{R}\)
und für \(R\to \infty\) konvergiert dieses Volumen gegen den endlichen Wert \(\pi\).
Für den Flächeninhalt der Mantelfläche kann man analog vorgehen: Für das Stück mit \(1\leq x \leq R\) ist die Mantelfläche
\(M(R)=2\pi\displaystyle\int\limits_1^R\frac{1}{x}\sqrt{1+\frac{1}{x^4}}\,\mathrm{d}x=2\pi\int\limits_1^R\dfrac{\sqrt{1+x^4}}{x^3}\,\mathrm{d}x\)
Dieses Integral lässt sich nicht mehr explizit berechnen, es ist aber
\(M(R)=2\pi\displaystyle\int\limits_1^R\dfrac{1}{x}\sqrt{1+\frac{1}{x^4}}\,\mathrm{d}x \geq 2\pi\int\limits_1^R\dfrac{1}{x}\,\mathrm{d}x = 2\pi \ln(R).\)
Dieser Wert und damit auch der Flächeninhalt strebt für \(R\to\infty\) gegen unendlich. Trotz des endlichen Volumens ist die Mantelfläche also unendlich groß!
Am Ende des Kapitels haben Sie wieder die Wahl:
