1.4 Kombinatorik: Die Kunst des Abzählens (Fortsetzung)

Der Binomische Satz

Klassischer Schulstoff sind die Binomischen Formeln, die man durch Ausmultiplizieren und Zusammenfassen gleicher Terme findet:

Graphisch lässt sich die erste Identität so veranschaulichen:

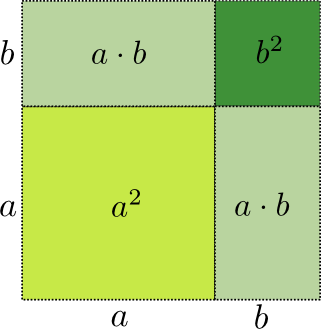
Die zweite Formel ergibt sich übrigens aus der ersten, indem man statt b die Zahl -b verwendet:

\((a-b)^2=(a+(-b))^2=a^2+2a(-b)+(-b)^2=a^2-2ab+b^2.\)

Das Ausmultiplizieren geht auch für höhere Potenzen:

\(\begin{array}{rcl}(a+b)^3 & = & a^3+3a^2b+3ab^2+b^3\\ (a+b)^4 & =& a^4+4a^3b+6a^2b^2+4ab^3+b^4\\ (a+b)^5 & = & a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5\end{array}\)

sieht dann allerdings immer komplizierter aus.

Wie oben kann man auch eines der Vorzeichen ändern und erhält

\(\begin{array}{rcl} (a-b)^3& =& (a+(-b))^3=a^3+3a^2(-b)+3a(-b)^2+(-b)^3\\ & =& a^3-3a^2b+3ab^2-b^3\\ (a-b)^4 & = & a^4-4a^3b+6a^2b^2-4ab^3+b^4\\ (a-b)^5 & = & a^5-5a^4b+10a^3b^2-10a^2b^3+5ab^4-b^5\end{array}\)

Es wäre praktisch, wenn man diese Formeln auch ohne Ausmultiplizieren erhalten könnte, also direkt hinschreiben könnte, was \((a+b)^6\) ausmultipliziert ergibt. Als kleine Vorüberlegung schauen wir noch einmal genau an, was beim Ausmultiplizieren passiert

\(\begin{array}{rcl}(a+b)^5&=&(a+b)(a+b)(a+b)(a+b)(a+b)\\&=&a\cdot a\cdot a\cdot a\cdot a+a\cdot a\cdot a\cdot a\cdot b+a\cdot a\cdot a\cdot b\cdot a+\dots\\&=&\dots\\&=&a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5\end{array}\)

Zunächst stellt man fest, dass nur Terme \(a^5\), \(a^4 b\), \(a^3 b^2\), \(a^2b^3\), \(ab^4\) und \(b^5\) vorkommen, also solche, bei denen die Summe der Exponenten genau fünf ergibt. Das liegt daran, dass man aus jeder der fünf Klammern einen Faktor (ein "\(a\)" oder ein "\(b\)") auswählt. Die entscheidende Frage ist dann nur noch, wieviele Terme von jeder Sorte in der Summe vorkommen. Um die Antwort darauf zu finden, verfolgen wir die Idee noch etwas genauer, dass Ausmultiplizieren bedeutet, aus jeder Klammer entweder den Faktor \(a\) oder den Faktor \(b\) auszuwählen. Zum Beispiel gibt es

• nur einen Term \(a^5\), da dazu in jeder Klammer "\(a\)" gewählt werden muss

• \(5\) Terme der Form \(a^4 b\): das eine "\(b\)" kann aus jeder der fünf Klammern stammen

• \(10\) Terme der Form \(a^3 b^2\): die beiden "\(b\)"s kann man auf \({5\choose 2}\) Arten aus den fünf Klammern wählen

Binomialkoeffizienten spielen also eine entscheidende Rolle: Für einen Term \(a^k b^{5-k}\) muss man die \(k\) Klammern auswählen, aus denen man ein "‘\(a\)"’ nimmt, aus den restlichen \(n-k\) Klammern nimmt man dann das "‘\(b\)"’. Auf diese Weise erhält man

\((a+b)^5=a^5+\left(\begin{array}{c}5\\1\end{array}\right)a^4b+\left(\begin{array}{c}5\\2\end{array}\right)a^3b^2+\left(\begin{array}{c}5\\3\end{array}\right)a^2b^3+\left(\begin{array}{c}5\\4\end{array}\right)ab^4+b^5\)

was (zum Glück) genau mit unserem direkten Ausmultiplizier-Ergebnis von oben übereinstimmt.

Mit einer beliebigen Zahl \(n\) statt \(5\) und denselben Argumenten kann man dann Folgendes zeigen.

Für jede beliebige natürliche Zahl \(n\) gilt:

\((a+b)^n=a^n+\left(\!\begin{array}{c}n\\1\end{array}\!\right)a^{n-1}b+\left(\!\begin{array}{c}n\\2\end{array}\!\right)a^{n-2}b^2+\dots+\left(\!\begin{array}{c}n\\n-1\end{array}\!\right)ab^{n-1}+b^n.\)

Definiert man noch für jede natürliche Zahl \(n\), dass \({n\choose 0} = 1\) ist, dann wird daraus

Für \(n > 5\) hätten wir vermutlich bald Platzprobleme bekommen. Um diese Schwierigkeiten zu umgehen gibt es eine elegante Schreibweise für lange Summen: das Summenzeichen.

Die Schreibweise

\((a+b)^n=\sum\limits_{k=0}^n\left(\begin{array}{c}n\\k\end{array}\right)a^{n-k}b^k\)

heißt: Man lässt \(k\) von \(0\) bis \(n\) laufen, setzt also jede dieser Zahlen einmal für \(k\) ein und addiert alle Ergebnisse:

• mit \(k=0\): \(\left(\begin{array}{c}n\\0\end{array}\right)a^{n-0}b^0 = a^n\)

• mit \(k=1\): \(\left(\begin{array}{c}n\\1\end{array}\right)a^{n-1}b^1= na^{n-1}b\)

• mit \(k=2\): \(\left(\begin{array}{c}n\\2\end{array}\right)a^{n-2}b^2\)

• usw.

• mit \(k=n\): \(\left(\begin{array}{c}n\\n\end{array}\right)a^{n-n}b^n= b^ n\)

Die so erhaltenen n+1 Terme werden abschließend addiert.