11.7 Die Hyperbelfunktionen
11.7 Die Hyperbelfunktionen
\(
\begin{array}{rcl}\cosh( x)&:=&\displaystyle\frac{e^x+e^{-x}}{2}\\ &&\\ \sinh( x)&:=&\displaystyle\frac{e^x-e^{-x}}{2}\\&&\\ \tanh( x)&:=&\displaystyle\frac{\sinh(x)}{\cosh( x)}=\displaystyle\frac{e^x-e^{-x}}{e^x+e^{-x}}=1-\displaystyle\frac{2e^{-2x}}{1+e^{-2x}}\end{array}
\)
Viele Identitäten der Hyperbelfunktionen erinnern an die Eigenschaften von Sinus und Cosinus:
\(\begin{array}{rcl} \cosh( x+y)&=&\cosh( x)\cdot\cosh( y)+\sinh( x)\cdot\sinh( y)\\ &&\\\sinh( x+y)&=&\sinh( x)\cdot\cosh( y)+\cosh( x)\cdot\sinh( y)\\ &&\\\cosh^2( x)-\sinh^2( x)&=&1\end{array}\)
Herleitung: Direkt aus der Definition erhält man
\( \begin{array}{rcl}\cosh ( x)\cdot \cosh ( y)+ \sinh ( x) \cdot \sinh ( y) & =&\displaystyle\frac{e^x+e^{-x}}{2}\displaystyle\frac{e^y+e^{-y}}{2}+\displaystyle\frac{e^x-e^{-x}}{2}\displaystyle\frac{e^y-e^{-y}}{2}\\&&\\&=&\displaystyle\frac{2e^xe^y+2e^{-x}e^{-y}}{4}\\&=&\cosh (x+y)\end{array}\)
und
\( \begin{array}{rcl}\sinh ( x)\cdot\cosh( y)+\cosh( x)\cdot\sinh( y)&=&\displaystyle\frac{e^x-e^{-x}}{2}\displaystyle\frac{e^y+e^{-y}}{2}+\displaystyle\frac{e^x+e^{-x}}{2}\displaystyle\frac{e^y-e^{-y}}{2}\\&&\\&=&\displaystyle\frac{2e^xe^y-2e^{-x}e^{-y}}{4}\\&=&\sinh( x+y)\end{array} \)
und
\( \begin{array}{rcl}\cosh^2( x)-\sinh^2( x)&=&\displaystyle\frac{e^x+e^{-x}}{2}\displaystyle\frac{e^x+e^{-x}}{2}-\displaystyle\frac{e^x-e^{-x}}{2}\displaystyle\frac{e^x-e^{-x}}{2}\\&&\\&=&\displaystyle\frac{2e^xe^{-x}+2e^{x}e^{-x}}{4}=1.\end{array} \)
Allerdings sehen die Schaubilder der Hyperbelfunktionen anders aus als diejenigen der trigonometrischen Funktionen:
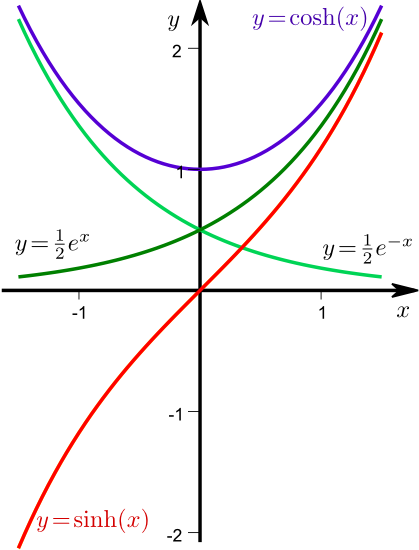
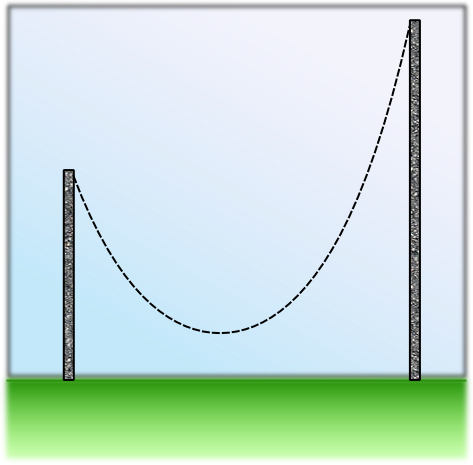Auch wenn wir dies hier noch nicht begründen können, sei trotzdem schon auf das Vorkommen des Cosinus hyperbolicus als Kettenlinie hingewiesen: Die Kurve, die eine zwischen zwei Pfosten frei hängende Kette beschreibt, ist gerade das Schaubild des Cosinus Hyperbolicus. Dabei spielt es keine Rolle, ob die "Aufhängepunkte" auf derselben Höhe oder unterschiedlich hoch angebracht sind.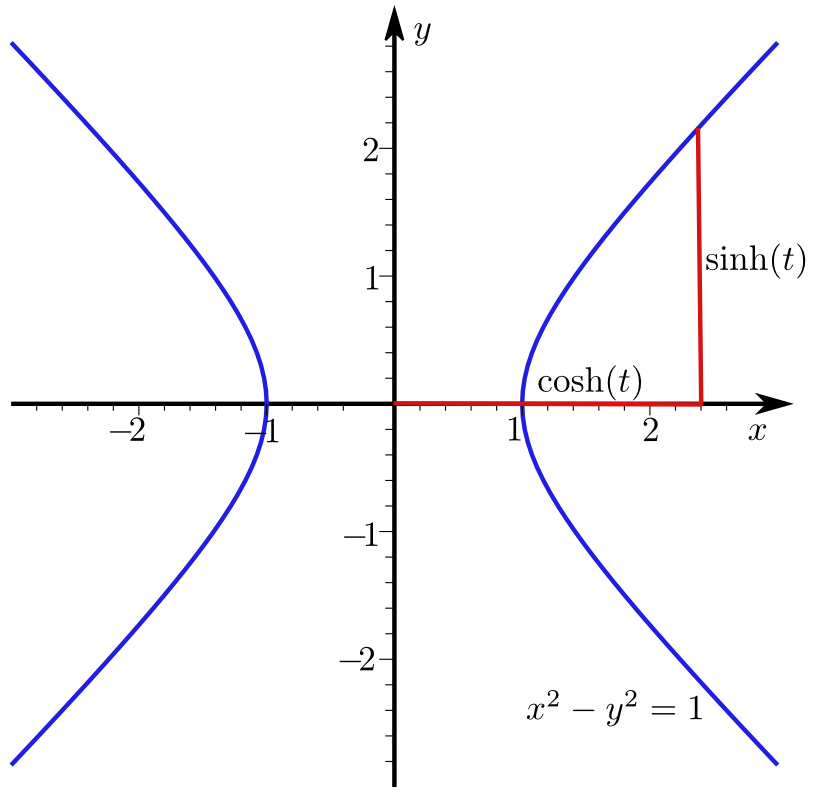
Hier ist wieder ein Kapitel zu Ende und Sie haben die Wahl: