10.1 Einleitung
10.1 Einleitung: Folgen und Grenzwerte
Funktionen sind ein wesentliches Hilfsmittel zur quantitativen Beschreibung vieler Zusammenhänge und Vorgänge: Aus der Schule kennen Sie das Ohmsche Gesetz, nach dem der in einer Leitung fließende Strom eine Funktion von Spannung und Widerstand ist.
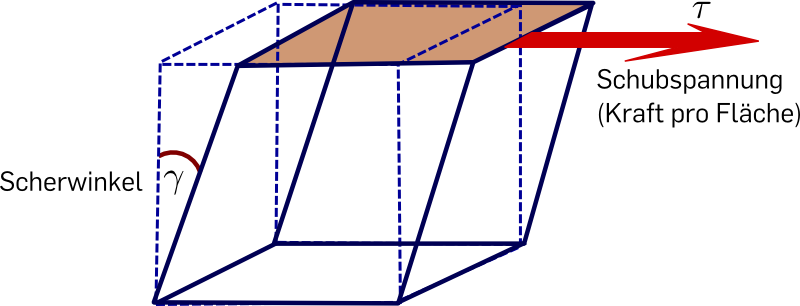
In der Mechanik ist die Schubspannung
\(\tau=G\cdot\tan(\gamma)\)
eine Funktion des Schubmoduls \(G\) und des Schubwinkels \(\gamma \).
In vielen Situationen treten lineare Funktionen auf, die die Proportionalität zwischen verschiedenen Größen beschreiben, aber oft ist dieser lineare Zusammenhang nur für einen gewissen Bereich gültig und muss durch einen kompliziertere Funktion ersetzt werden, wenn man diesen Bereich überschreitet.
Einige Eigenschaften der Funktionen erkennt man am besten, wenn man sich bestimmte Grenzfälle anschaut. Beispielsweise wird der \(\tan (\gamma )\) sehr groß, wenn der Winkel \(\gamma \) sich dem Wert \(\displaystyle\frac {\pi }{2}\) annähert. Das entspricht anschaulich der Vorstellung, dass man eine immer größere Kraft aufwenden muss, um den Scherwinkel zu vergrößern,
Umgekehrt kann man aber auch den Grenzwert kleiner Scherwinkel \(\gamma\) betrachten, zum Beispiel wenn \(\gamma<10^\circ\) ist. Dort unterscheiden sich \(\tan (\gamma )\) und der Winkel \(\gamma\) nur wenig und bei vielen Rechnungen kann man sich das Leben leichter machen, wenn man statt mit \(\tan (\gamma )\) nur mit \(\gamma \) rechnet.
Wie in diesem Fall gibt es viele Situationen, in denen Grenzübergänge eine komplizierte Situation oder Rechnung vereinfachen.
Grenzwerte von Funktionen
Ein Behälter wird nach DIN 2413 als dünnwandig bezeichnet, falls das Verhältnis zwischen Wandstärke \(s\) und Innendurchmesser \(d_ i\) kleiner als \(0,1\) ist. Herrscht im Inneren eines abgeschlossenen, zylinderförmigen dünnwandigen Behälters ein Überdruck \(p_ i\) so führt dies zu einer Ausdehnung und damit verbunden zu Spannungen in der Wand. Die Tangentialspannung \(\sigma _ t=\displaystyle\frac {p_ i\cdot d_ i}{2s}\) wirkt in Richtung
Die axiale Spannung \(\sigma _ a\) in Richtung der Zylinderachse
Bei dünnwandigen Behältern setzt man voraus, dass diese Spannung innerhalb der Wand konstant ist.
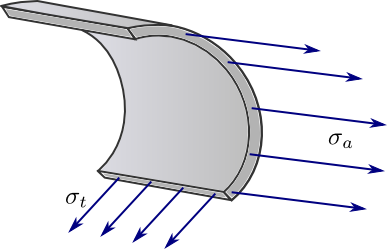
Aus einer Gleichgewichtsbedingung ergibt sich dann die Gleichung
\(\begin{array}{rcl}p_i\underbrace{\displaystyle\frac{\pi}{4}d_i^2}_{\text{innere Querschnittsfläche }}&=&\sigma_a\cdot\underbrace{\displaystyle\frac{\pi}{4}((d_i+s)^2-d_i^2)}_{\text{Querschnittsfläche der Wand}}\\&=&\sigma_a\cdot\displaystyle\frac{\pi}{4}(d_i^2+4sd_i+4s^2-d_i^2)\\ \Leftrightarrow p_id_i^2&=&\sigma_a\cdot(4sd_i+4s^2)\\ \Leftrightarrow\sigma_a&=&\displaystyle\frac{p_id_i^2}{4sd_i+4s^2}\end{array}\)
Nun ist \(s\) viel kleiner als \(d_ i\) und damit \(4s^2\) auch viel kleiner als \(4sd_ i\).
Beim Grenzübergang \(s\to 0\) ("Wanddicke ist vernachlässigbar klein gegenüber dem Kesseldurchmesser") kann man den Term \(4s^2\) daher vernachlässigen (=weglassen). Dies führt auf die wesentlich einfachere "‘Kesselformel"’
\(\sigma_a=\displaystyle\frac{p_id_i}{4s}=\displaystyle\frac{\sigma_t}{2}\)
Dieser Zusammenhang zwischen \(\sigma _ a\) und \(\sigma _ t\) hat übrigens eine recht anschauliche Auswirkung: Bratwürste platzen beim Erhitzen auf dem Grill immer in Längsrichtung auf, da die Umfangsspannung doppelt so groß ist wie die Spannung in Längsrichtung.
Wie in diesem Beispiel helfen Grenzwertbetrachtungen in vielen Fällen unter mehreren Effekten denjenigen auszusondern, der für dünne Wände, lange Seile, große Biegesteifigkeit, etc. den entscheidenden Beitrag liefert. Grenzwerte spielen eine wichtige Rolle, wenn es darum geht, sinnvolle Vereinfachungen durchzuführen. Darüber hinaus erlauben Sie auch zu quantifizieren, welche Fehler bei diesen Vereinfachungen auftreten.
