14.2 Der Hauptsatz der Differential- und Integralrechnung
14.2 Der Hauptsatz der Differential- und Integralrechnung
Leibniz und Newton erkannten im 17. Jahrhundert, dass die Flächenberechnung und die Bestimmung der Tangente in gewisser Weise zueinander invers sind. Anstatt mühsam Riemannsummen aufzuaddieren, kann man daher versuchen, die Umkehrung der Differentiation zu bilden. In moderner Sprechweise lautet die Aussage dieses fundamentalen Satzes
Sei \([a,b]\subset \mathbb {R}\) ein abgeschlossenes Intervall und \(f\colon[a,b]\to \mathbb {R}\) eine stetige Funktion. Dann ist die Funktion \(F\colon[a,b]\to \mathbb {R}\) mit
\(F(x)=\displaystyle\int\limits_a^x f(t)\,\mathrm{d}t\)
differenzierbar im Intervall \((a,b)\) und für alle \(x\in (a,b)\) gilt \(F’(x)=f( x)\).
Beweis: Sei \(x_0\in (a,b)\) beliebig. Wir betrachten den Differenzenquotienten
\(\lim\limits_{h\to 0}\displaystyle\frac{F(x_0+h)-F(x_0)}{h}=\lim\limits_{h\to 0}\displaystyle\frac{1}{h}\left(\displaystyle\int\limits_a^{a+x_0}f(t)\,\mathrm{d}t-\int\limits_a^{a+x_0+h}f(t)\,\mathrm{d}t\right)=\lim\limits_{h\to 0}\displaystyle\frac{1}{h}\displaystyle\int\limits_{x_0}^{x_0+h}f( t)\,\mathrm{d}t,\)
wobei \(h>0\) ist. Nach dem Mittelwertsatz existiert ein \(\xi_h\in [x_0,x_0+h]\) mit
\(\displaystyle\int\limits_{x_0}^{x_0+h}f(t)\,\mathrm{d}t=hf(\xi_h).\)
Da \(f\) in \(x_0\) stetig ist, und für \(h\to 0\) die "Zwischenstelle" \(\xi \) immer näher an \(x_0\) heranrückt, ist \(\lim\limits_{h\to 0}f(\xi_h)=f( x_0)\), also
\(\lim\limits_{h\to 0}\displaystyle\frac{F( x+h)-F( x)}{h}=\lim\limits_{h\to 0}\displaystyle\frac{1}{h}\int\limits_x^{x+h}f( t)\,\mathrm{d}t=\lim\limits_{h\to 0}\displaystyle\frac{1}{h}hf(\xi_h)=f(x).\)
Für \(h<0\) ist das Argument ganz analog, wenn man berücksichtigt, dass in diesem Fall
\(F( x+h)-F( x)=\displaystyle\int\limits_{x_0+h}^{x_0}f( x)\,\mathrm{d}x.\)
?
Das folgende Geogebra-Applet erlaubt es, zu vielen Funktionen die Stammfunktion graphisch darzustellen und mit dem Flächeninhalt unter dem Graph einer Funktion zu vergleichen.
Flächeninhalt und Stammfunktion - GeoGebra Dynamisches Arbeitsblatt
Applet: Flächeninhalt und Stammfunktion
Anleitung: In der Eingabezeile kann mit f(x)=x^2-2 oder f(x)=sin(2*x) oder einer anderen Definition die Funktion f festgelegt werden, die Integralgrenzen können durch Ziehen von a und b mit der Maus bewegt werden.
J.H., erstellt mit GeoGebra
Die Kenntnis von einigen Ableitungen hilft uns, unmittelbar einige Integrale zu berechnen:
\(\begin{array}{rcl}\displaystyle\int x^n\,\mathrm{d}x&=&\displaystyle\frac{x^{n+1}}{n+1}\\ \int e^{\alpha x}\,\mathrm{d}x&=&\displaystyle\frac{1}{\alpha}e^{\alpha x}\\ \int\displaystyle\frac{1}{x}\,\mathrm{d}x&=&\ln(x)\\\int\displaystyle\frac{\mathrm{d}x}{1+x^2}\,&=&\arctan(x)\\ \int\displaystyle\frac{\mathrm{d}x}{\sqrt{1-x^2}}\,&=&\arcsin(x)\end{array}\)
Sei \(f\) eine stetige Funktion. Dann ist die Differenz von zwei beliebigen Stammfunktionen von \(f\) konstant.
Beweis: Seien \(G_1\) und \(G_2\) zwei Stammfunktionen von \(f\). Nach Definition der Stammfunktion ist dann \(G_1’=f=G_2’\), also \(G_1’-G_2’=(G_1-G_2)’=0\). Nach dem Mittelwertsatz ist \(G_1-G_2\) also konstant, konkret \(G_1(x)-G_2(x)=C\) für eine Konstante \(C\in \mathbb {R}\).
Wir wissen schon, dass durch \(F(x):=\int \limits _ a^ xf(t)\, \mathrm{d}t\) eine Stammfunktion gegeben ist. Also sind alle möglichen Stammfunktionen von der Form \(\int \limits _ a^ xf(t)\, \mathrm{d}t +C\) mit einer beliebigen Konstante \(C\in \mathbb {R}\).
Bemerkung:
Manchmal wird als unbestimmtes Integral von \(f\) auch die Menge aller Stammfunktionen von \(f\) bezeichnet. Man schreibt dann
\(\int f( x)\,\mathrm{d}x = F( x) + C,\)
um klarzumachen, dass \(F( x)+C\) f\"ur jedes \(C\in\mathbb{R}\) eine Stammfunktion ist. Die Konstante \(C\) nennt man Integrationskonstante.
Dies hilft uns nun auch bei der Berechnung bestimmter Integrale: Satz:
Sei \(f\colon[a,b]\to \mathbb {R}\) stetig und \(G\) (irgend-)eine Stammfunktion von \(f\). Dann ist
\(\int\limits_a^bf( x)\,\mathrm{d}x=G(b)-G(a).\)
Beweis: Wir betrachten zunächst die Stammfunktion \(F(x)=\int \limits _ a^ xf(t)\, \mathrm{d}t\), die wir schon kennen. Für diese gilt \(F(a)=0\) und \(F(b)=\int \limits _ a^ bf(t)\, \mathrm{d}t\). Da \(F(x)-G(x)=C\) für alle \(x\), ist insbesondere \(F( a)-G( a)=C=F( b)-G( b)\) und damit \(G(b)-G(a)=F( b)-F(a)=\int\limits_a^b f(x)\,\mathrm{d}x.\)
□
Für die Auswertung einer Stammfunktion zwischen den Grenzen \(a\) und \(b\) wird oft
\(\int\limits_a^bf(x)\,\mathrm{d}x=G(x)\bigg|_a^b\)
geschrieben.
Im allerersten Kapitel wurde ein Rotorblatt approximiert durch einen Stab der Länge \(L\) mit Querschnitt \(A\) und Dichte \(\varrho \), der mit der Winkelgeschwindigkeit \(\omega \) rotiert.
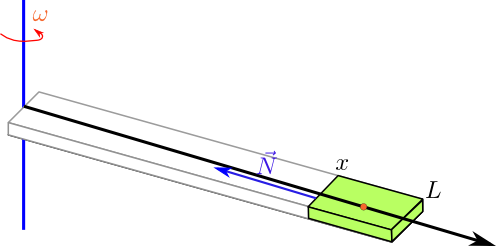
Die Normalkraft, die im Abstand \(x\) von der Drehachse im Rotorblatt nach innen wirkt, beträgt
\(|\vec{N}|=mr\omega^2=\varrho(L-x)A\cdot\frac{1}{2}(L+x)\cdot\omega^2=\frac{1}{2}\varrho A\omega^2(L^2-x^2).\)
und bewirkt eine Spannung
\(\sigma(x)=\displaystyle\frac{|\vec{N}|}{A}=\frac{1}{2}\varrho\omega^2(L^2-x^2),\)
die wiederum eine Längenänderung \(\varepsilon =\frac{1}{E}\sigma \) verursacht, wobei \(E\) der Elastizitätsmodul ist. Da die Spannung von Punkt zu Punkt verschieden ist, muss man die Gesamtverlängerung des Rotorblatts durch Integration bestimmen:
\(\Delta L=\int\limits_0^L\varepsilon(x)\,\mathrm{d}x=\int\limits_0^L\frac{1}{E}\frac{1}{2}\varrho\omega^2(L^2-x^2)\,\mathrm{d}x=\left.\frac{1}{E}\frac{1}{2}\varrho\omega^2(L^2x-\frac{x^3}{3})\right|_{x=0}^L=\frac{1}{E}\frac{1}{3}\varrho\omega^2L^3.\)
Ein wesentlicher Unterschied zwischen dem Differenzieren und dem Integrieren unbekannter Funktionen besteht darin, dass man die Ableitung in den meisten Fällen durch die korrekte Anwendung einiger weniger Regeln berechnen kann, während es bei der Integration kein solch klares Vorgehen gibt.
Das Ziel bei der Integration besteht in vielen Fällen darin, ein gegebenes unbekanntes Integral durch Umformungen in eines oder mehrere Integrale zu überführen, die man schon kennt (weil sie in der obigen Liste enthalten sind).