Betrachte einen langen Balken (d.h. Querschnittsabmessungen \(\ll \) Länge \(L\)), der am Ende mit einer Kraft \(\vec{F}\) belastet wird. Nach der Bernoulli-Hypothese bleiben Querschnitte, die im unverformten Balken senkrecht auf die Balkenachse stehen, während der Deformation eben und senkrecht zur verformten Balkenachse:

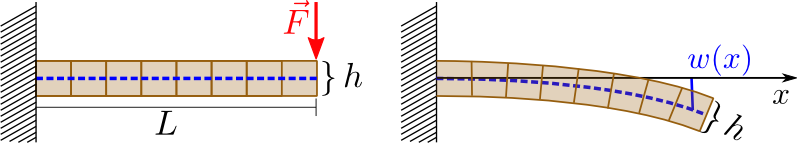
Man kann das Problem daher als eindimensionale Fragestellung behandeln. Die Biegelinie \(w(x)\), also die Auslenkung der neutralen Faser gegenüber dem unverformten Zustand, wird bei einem rechteckigen Balken beschrieben durch die Differentialgleichung

\(w”(x)=-\displaystyle\frac{M}{EI}\)

wobei \(M\) das Biegemoment und \(E I\) die Biegesteifigkeit (= das Produkt aus dem Elastizitätsmodul \(E\) und dem Flächenträgheitsmoment \(I\)) des Balkens ist. Durch Ableiten ergeben sich die Gleichungen

\(\begin{array}{rcl}EIw”’(x)&=&-M’(x)=-Q(x)\;\;\text{(Querkraft)}\\EIw””(x)&=&-Q’(x)\,=\;q(x)\;\;\text{(Streckenlast)}\end{array}\)

Bei einem einseitig fest eingespannten Balken ist \(q=0\), wir erhalten daher durch Integration

\(\begin{array}{rcl}EIw””(x)=0&\Rightarrow&EIw”’(x)=EI\int w””(x)\,\mathrm{d}x=C_1\\&&\\&\Rightarrow&EIw”(x)=EI\int w”’(x)\,\mathrm{d}x=C_1x+C_2\\&&\\&\Rightarrow&EIw’(x)=EI\int w”(x)\,\mathrm{d}x=\frac{1}{2}C_1x^2+C_2x+C_3\\&&\\ &\Rightarrow& EIw(x)=EI\int w’(x)\,\mathrm{d}x=\frac{1}{6}C_1x^3+\frac{1}{2}C_2x^2+C_3x+C_4\end{array}\)

Die Integrationskonstanten \(C_1,\dots ,C_4\) ergeben sich aus den Randbedingungen:

Keine Verschiebung an der Einspannung: \(\quad w(x=0)=0 \;\; {\Rightarrow }\; C_4=0\)
Keine Biegung an der Einspannung: \(\quad w’(x=0)=0 \;\; {\Rightarrow }\; C_3=0\)
Querkraft am Balkenende: \(Q(x=L)=|\vec{F}|=F \;\; {\Rightarrow }\; C_1=-F\)
Kein Biegemoment am Balkenende: \(M(x=L)= -EIw”(L)=0 \;\; {\Rightarrow }\; C_2=F{\cdot }L\)

Damit ist \(EI w(x)= -\displaystyle\frac {F}{6} x^3 + \displaystyle\frac {FL}{2} x^2 \), die Absenkung am Balkenende beträgt also

\(w(L)=-\displaystyle\frac{F}{6EI}L^3+\displaystyle\frac{FL}{2EI}L^2=\displaystyle\frac{FL^3}{3EI}.\)