11.4 Die Logarithmusfunktion
11.4 Die Logarithmusfunktion
Wir haben gesehen, dass die Exponentialfunktion \(\exp :\mathbb {R}\to (0,\infty )\) streng monoton wachsend ist und alle Werte im Intervall \((0,\infty)\) annimmt. Daher besitzt die Exponentialfunktion eine Umkehrfunktion.
\(y=\ln( x){\quad}\Leftrightarrow{\quad}x=e^y\)
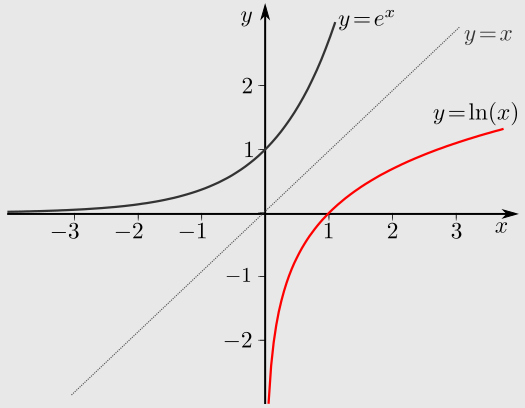
Die Logarithmusfunktion ist ebenfalls streng monoton wachsend und aus den speziellen Werten der Exponentialfunktion ergeben sich die speziellen Werte
\(\ln(1)=0,\qquad\ln(e)=1.\)
Kleinere Flugzeug haben üblicherweise keine Messgeräte, die die Flughöhe direkt messen, sondern verwenden dafür die barometrische Höhenmessung . Weil man weiß, wie der Luftdruck als Funktion der Höhe über dem Boden abnimmt, kann man umgekehrt aus dem gemessenen Luftdruck die Flughöhe bestimmen. Die barometrische Höhenformel besagt, dass bei einem Luftdruck \(p_0\) auf der Höhe \(h_0=0\) der Druck auf der Höhe \(h\) durch
\(p( h)=p_0e^{-\displaystyle\frac{\rho_0}{p_0}gh}\)
gegeben ist, wobei \(\rho _0\) die Dichte auf der Höhe \(0\) und \(g\approx 10\frac{m}{s^2}\) die Erdbeschleunigung ist. Die Umkehrfunktion kann mit Hilfe der Logarithmusfunktion explizit bestimmt werden und ergibt als Höhe\(h( p)=\displaystyle\frac{p_0}{\rho_0 g}\cdot\ln\left(\displaystyle\frac{p_0}{p}\right)\)
in Abhängigkeit des gemessenen Drucks \(p\).
Aus den Rechenregeln für Potenzen (den Potenzgesetzen ) kann man entsprechende Regeln für das Rechnen mit Logarithmen herleiten.
Begründung: Ausgangspunkt ist das Potenzgesetz
\(\underbrace{e^a}_{=x}\cdot\underbrace{e^b}_{=y}=\underbrace{e^{a+b}}_{=x\cdot\,y}.\)
Nach Definition des Logarithmus ist wegen \(a=\ln (x)\), \(b=\ln ( y)\) und \(a+b=\ln ( x\,\cdot\,y)\)
\(\ln(x)+ \ln(y)=\ln( x\,\cdot\,y).\)
Für die dritte Identität beginnen wir mit dem Potenzgesetz
\(\left(\underbrace{e^a}_{=x}\right)^n=\underbrace{e^{n\cdot\,a}}_{=y}\)
Nach der Definition des Logarithmus ist dann \(a=\ln (x)\) und \(n\cdot a=\ln( y)\). Aus der Gleichung \(y=x^n\) erhält man damit
\(n\cdot\ln( x)=\ln( y)=\ln( x^n).\)
Die anderen Identitäten lassen sich auf ähnliche Weise aus den Potenzgesetzen herleiten.
☐
Beweis: Der Grenzwert lässt sich zurückführen auf den schon bekannten Grenzwert
\(\displaystyle\lim\limits_{t\to-\infty}te^t=0,\) ("Die Exponentialfunktion gewinnt immer")
indem man \(x=e^ t\) setzt. Dann ist
\(\displaystyle\lim\limits_{x\to\infty}\displaystyle\frac{\ln(x)}{x^n}=\lim\limits_{t\to\infty}\displaystyle\frac{\ln(e^t)}{(e^t)^n}=\lim\limits_{t\to\infty}\displaystyle\frac{t}{e^{nt}}=\lim\limits_{t\to\infty}\displaystyle\frac{t}{e^{nt}}=\lim\limits_{t\to\infty}te^{-nt}=0\)
☐