3.1 Darstellung von Geraden
In einer Ebene E mit einem kartesischen Koordinatensystem lässt sich eine Gerade g durch eine lineare Gleichung für die Koordinaten x und y beschreiben: Alle Punkte (x,y), die auf der Gerade liegen, erfüllen die lineare Gleichung
\(y = mx + b\)
mit geeigneten Zahlen m und b. Umgekehrt beschreibt jede solche lineare Gleichung eine Gerade in der Ebene.
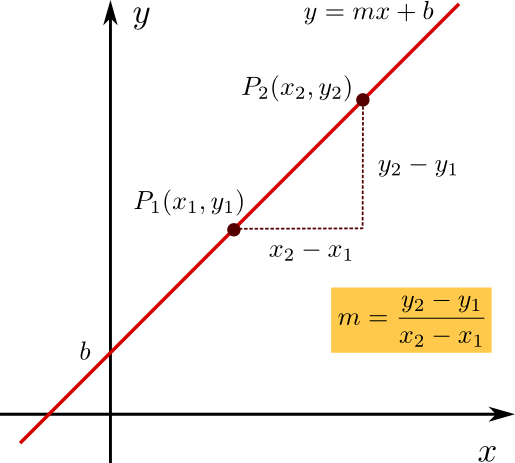
Die beiden Größen m und b haben eine anschauliche Bedeutung:
-
\(m\) ist die Steigung der Geraden
-
\(b\) ist der Achsenabschnitt, d.h. die Gerade schneidet die y-Achse im Punkt \((0,b)\).
Allerdings gibt es Geraden, die sich so nicht darstellen lassen, nämlich alle Geraden, die parallel zur -Achse verlaufen. Wir werden daher noch andere Darstellungsformen untersuchen, die es erlauben, alle Geraden auf eine einheitliche Art zu schreiben.
Bei der Bestimmung von Geradengleichungen begegnet man verschiedenen Aufgabenstellungen.
-
Sind zwei Punkte \(P_0\) und \(P_1\) auf der Geraden \(g\) bekannt, so ergeben sich die zugehörigen Werte m und b, indem man ausnutzt, dass die Koordinaten der Punkte \(P_1 = (x_1, y_1)\) und \(P_2 = (x_2, y_2)\) die Gleichung \(y=mx + b\) erfüllen. Dies führt auf zwei Gleichungen mit den zwei Unbekannten \(m\) und \(b\):
\(\begin{array}{rcl}y_1&=&mx_1+b\\y_2&=&mx_2+b\end{array}\)
aus denen man dann die Werte
\(m=\displaystyle\frac{y_2-y_1}{x_2-x_1}\;\) und \(\;b=y_1-\displaystyle\frac{y_2-y_1}{x_2-x_1}x_1\)
erhält. Man kann allerdings auch die Geradengleichung direkt hinschreiben:
\(y-y_1=\displaystyle\frac{y_2-y_1}{x_2-x_1}(x-x_1)\)
Diese Gleichung stellt sicher, dass der Punkt \((x_1, y_1)\) auf der Geraden liegt, denn setzt man für \(x\) den Wert \(x_1\) und für \(y\) den Wert \(y_1\) ein, dann steht auf beiden Seiten der Gleichung Null. Da auch die Steigung mit der Steigung einer Gerade durch die Punkte \(P_1 = (x_1, y_1)\) und \(P_2 = (x_2, y_2)\) übereinstimmt, liegt auch der zweite Punkt \(P_2 = (x_2, y_2)\) auf der Geraden.
-
Ist die Gerade durch einen Punkt \(P_1 = (x_1, y_1)\) und die Steigung \(m\) gegeben, so erhält man die noch fehlende Größe \(b\), indem man benutzt, dass die Koordinaten des Punktes \(P_1 = (x_1, y_1)\) die Gleichung \(y = mx + b\) erfüllen müssen. Noch einfacher ist es, die Gleichung in der Form
\(y-y_1=m(x-x_1)\)
beziehungsweise\(y=m x \,\underbrace{-m x_1+ y_1}_{=b}\)
direkt hinzuschreiben, bei der man sofort sieht, dass sie für \(y=y_1\) und \(x=x_1\) erfüllt ist, denn in der Version \(y-y_1=m(x-x_1)\) sind dann beide Seiten gleich Null.
Hier eine kleine Aufgabe zu diesem Thema:
Wie man Geradengleichungen mit Hilfe von Vektoren darstellt, siehst Du
