4.2 Das Gaußsche Eliminationsverfahren

In der Schule haben Sie möglicherweise schon gelernt, wie man lineare Gleichungssysteme mit zwei oder drei Unbekannten lösen kann.

Beispielsweise kann man die Variablen der Reihe nach eliminieren, indem man eine Gleichung nach einer der Variablen auflöst und dann in die anderen Gleichungen einsetzt. Dieses bei Studierenden erfahrungsgemäß sehr beliebte Verfahren wird jedoch mit zunehmender Anzahl an Variablen immer komplizierter und ist schon für drei Gleichungen mit drei Unbekannten in der Regel nicht zu empfehlen.

Aus diesem Grund soll hier ein anderes Lösungsverfahren besprochen werden, das sich auch für größere Gleichungssystem eignet und das auch für die numerische Lösung von linearen Gleichungssystemen mit dem Computer implementiert werden kann.

Betrachten wir zunächst ein allgemeines lineares Gleichungssystem:

\(\begin{array}{rcl}a_{11}x_1+a_{12}x_2+\ldots+a_{1n}x_n&=&b_1\\a_{21}x_1+a_{22}x_2+\ldots+a_{2n}x_n&=&b_2\\\vdots\hspace{5em}&&\vdots\\a_{m1}x_1+a_{m2}x_2+\ldots+a_{mn}x_n&=&b_m\end{array}\)

Falls wir irgendwie eine Lösung \((x_1,x_2,\dots ,x_ n)\) gefunden haben, dann ist natürlich jede einzelne dieser Gleichungen erfüllt, zum Beispiel die k-te:

\(a_{k1}x_1+a_{k2}x_2+\ldots+a_{kn}x_n=b_k\)

Wir können die Gleichungen also vertauschen und in beliebiger Reihenfolge hinschreiben (dürfen dabei aber natürlich keine weglassen).

Auch wenn wir eine der Gleichungen mit einer Zahl \(\lambda \neq 0\) multiplizieren, bleibt die Gleichung richtig:

\({\lambda}a_{k1}x_1+{\lambda}a_{k2}x_2+\ldots+{\lambda}a_{kn}x_n={\lambda}b_k,\)

denn wir könnten ja diese Gleichung auch wieder durch \(\lambda\) teilen und hätten dann die ursprüngliche Gleichung zurück.

Man kann auch zwei der Gleichungen zueinander addieren, zum Beispiel die \(j\)-te und die \(k\)-te Gleichung, und erhält dann wieder eine gültige Gleichung:

\((a_{j1}+a_{k1})x_1+(a_{j1}+a_{k2})x_2+\ldots+(a_{jn}+a_{kn})x_n=(b_j+b_k)\)

Die letzten beiden Varianten lassen sich sogar miteinander kombinieren, indem man für Zahlen \(\mu \) und \(\lambda \neq 0\) das \(\mu \)-fache der \(j\)-ten Gleichung zum \(\lambda \)-fachen der \(k\)-ten Gleichung addiert.

\(({\mu}a_{j1}+{\lambda}a_{k1})x_1+({\mu}a_{j1}+{\lambda}a_{k2})x_2+\ldots+({\mu}a_{jn}+{\lambda}a_{kn})x_n=({\mu}b_j+{\lambda}b_k)\)

Diese Eigenschaften liegen dem Gauß-Verfahren zugrunde. Dabei geht es darum, mit Hilfe der sogenannten elementaren Zeilenumformungen , die genau den eben besprochenen Eigenschaften entsprechen, das Gleichungssystem in eine Form zu bringen, die es erlaubt, die Gleichungen der Reihe nach aufzulösen.

Ein Blick voraus: Matrizen

Eine ökonomische Methode, um das Gaußsche Eliminationsverfahren durchzuführen, besteht darin, gar nicht in jedem Schritt die Unbekannten \(x_1, x_2,\dots \) hinzuschreiben, sondern nur die Koeffizienten.

Diese notiert man sich in einer Matrix, d.h. statt des vollen Gleichungssystems

\(\begin{array}{rrrcl}-2x_1&+3x_2&-x_3&=&\phantom{-}3\\x_1&-2x_2&&=&-3\\5x_1&-\phantom{2}x_2&+x_3&=&-4\end{array}\)

schreibt man nur noch

\(\begin{array}{rrr|r}-2&+3&-1&3\\1&-2&0&-3\\5&-1&1&-4\end{array}\)

Dabei muss man darauf achten, für Unbekannte, die in einer Gleichung gar nicht auftauchen, den Koeffizienten \(0\) einzusetzen (hier in der zweiten Zeile der Koeffizient von \(x_3\)). Die Einträge der rechten Seite trennt man typischerweise durch einen vertikalen Strich von den Koeffizienten der Unbekannten.

Hier ein Beispiel zum Selbermachen: Wie sieht das entsprechende Zahlenschema für das lineare Gleichungssystem

\( \begin{aligned} 3x_1+ 5x_2 & = \phantom{-}17 \\ -x_2-4x_3 & = -3 \end{aligned} \)

aus?

Lösung:

\( \begin{array}{rrr|r} 3& 5& 0 & 17 \\ 0& -1 & -4 & -3 \end{array} \)

---

Unter Benutzung der drei erlaubten Operationen

• Vertauschen von Zeilen

• Multiplikation einer Zeile mit einer Zahl \(\lambda \neq 0\)

• Addition des \(\lambda \)-fachen einer Zeile zum \(\mu \)-fachen einer anderen Zeile

versucht man, das Gleichungssystem, bzw. die zugehörige Matrix in eine Form zu bringen, aus der man leichter ablesen kann, ob und ggf. welche Lösungen das Gleichungssystem besitzt. Ziel dabei ist es, die sogenannte Zeilenstufenform zu erreichen:

\(
\left(\begin{array}{ccccccc|r}
\alpha_1\dots\ast & \ast\dots\ast & \ast\dots\ast& \dots & \dots & \dots & \ast & \ast \\
0\dots 0 & \alpha_2\dots\ast & \ast\dots\ast & \dots & \dots & \dots & \ast & \ast \\
0\dots 0 & 0\dots 0 & \alpha_3\dots\ast & \dots & \dots & \dots & \ast & \ast \\
0\dots 0 & 0\ldots 0 & 0\ldots 0 & \ddots & \ddots & \ldots & \vdots & \vdots \\
{\vdots}\hspace{2em} \vdots & {\vdots}\hspace{2em} \vdots & \vdots\hspace{2em} \vdots & \ddots & \ddots & \ldots & \vdots & \vdots \\
0\dots 0 & 0\ldots 0 & 0\ldots 0 & 0\dots 0 & \ddots & \alpha_k & \ast & \ast \\
0\dots 0 & 0\ldots 0 & 0\ldots 0 & \ldots & 0 & \ldots & 0 & \ast \\
{\vdots}\hspace{2em} \vdots &{\vdots}\hspace{2em} \vdots & \vdots\hspace{2em} \vdots & \ldots & & \ldots & \vdots & \vdots \\
0\ldots 0 & 0\ldots 0 & 0\ldots 0 & \ldots & 0 & \ldots & 0 & \ast
\end{array}\right)
\)

Hierbei sind die Einträge \(\alpha _1, \alpha _2,\dots ,\alpha _ n\neq 0\) und an allen Stellen mit Stern darf eine beliebige Zahl stehen.

Die Zeilenstufenform heißt so, weil die Nullen und die von Null verschiedenen Einträge durch "‘Stufen"’ voneinander getrennt sind:

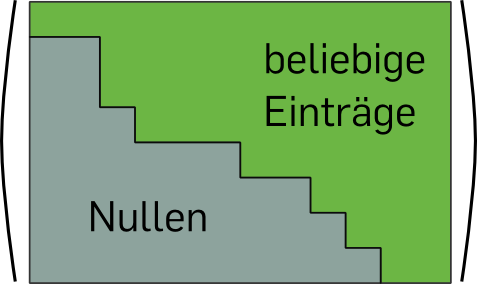
Schreibt man die Koeffizientenmatrix des linearen Gleichungssystems auf, das wir im allerletzten Schritt des Beispiels erhalten hatten, so lautet diese

\(A=\left(\begin{array}{rrr|r}1&-2&0&-3\\0&-1&-1&-3\\0&0&-8&-16\end{array}\right)\)

Aus diesem Schema kann man nun wie oben die Lösung des Gleichungssystems ablesen.

Auf der nächsten Seite sehen Sie ein konkretes Beispiel zum Gauß-Verfahren.