1.6 Funktionen (Fortsetzung)

Injektivität und Surjektivität

Definition (surjektiv, injektiv, bijektiv):
Eine Abbildung \(f:M\to N\) heißt

  • surjektiv, falls es zu jedem Element \(y\) von \(N\) mindestens ein \(x\in M\) gibt mit \(f( x)=y\).

  • injektiv, falls es zu jedem Element \(y\) von \(N\) höchstens ein \(x\in M\) gibt mit \(f( x)=y\).

  • bijektiv, falls \(f\) injektiv und surjektiv ist, d.h. falls es zu jedem Element \(y\) von \(N\) genau ein \(x\in M\) gibt mit \(f( x)=y\).

Bemerkung:
Andere (aber gleichwertige) Formulierungen sind:

  • \(f:M\to N\) ist surjektiv genau dann, wenn \(f(M)=N\) ist.

  • \(f:M\to N\) ist injektiv, wenn kein Element von \(N\) zwei verschiedene Urbilder besitzt, falls also

    \(a\neq b\Rightarrow f(a)\neq f(b)\) für alle \(a,b\in M.\)

    In Worten ausgedrückt heißt das, dass verschiedene Argumente auch verschiedene Funktionswerte liefern. Um Injektivität nachzuprüfen benutzt man gelegentlich die Umkehrung dieser Aussage: \(f\) ist genau dann injektiv, wenn für beliebige \(a,b \in M\)

    \(f(a)=f(b)\Rightarrow a=b\)

    gilt.

Beispiele

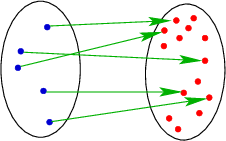
Injektive, aber nicht surjektive Abbildungen:

Sei \(M\) die Menge aller Studierenden der Ruhr-Uni. Die Abbildung \(f:M\to \mathbb {N}\) ordnet jedem Studierenden seine Matrikelnummer zu.

  • injektiv, denn keine zwei Studierende haben dieselbe Matrikelnummer

  • nicht surjektiv, denn nicht alle (natürlichen) Zahlen kommen als Matrikelnummer vor.

Schematisch dargestellt:

inj_notsurj

Surjektive, aber nicht injektive Abbildungen:

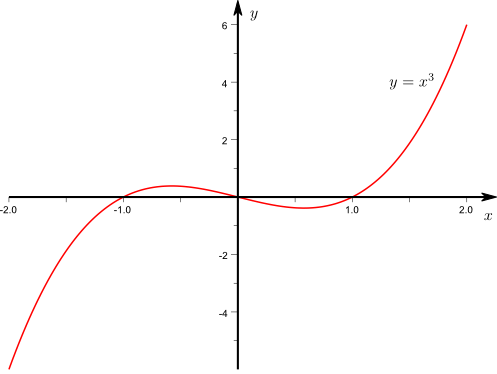
Die Abbildung \(k:\mathbb{R}\to \mathbb {R}\) mit \(q(x)=x^3-x\) ist

  • nicht injektiv , denn \(q(-1)=q(0)=q(1)=0\)

  • surjektiv , denn wenn man das Schaubild von \(q\) betrachtet, erkennt man, dass alle reellen Zahlen als Funktionwerte vorkommen

Kubische Parabel


Schematisch:

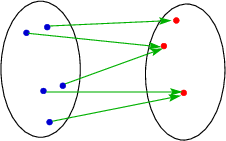
notinj_surj

Bijektive Abbildung:

Die Abbildung \(f:\mathbb {R}\to\mathbb{R}\), die jeder reellen Zahl \(x\) die Zahl \(f(x)=2x-1\) zuordnet ist

    • injektiv und surjektiv

denn zu \(f(x)=y\) kann man sich auf eindeutige Weise das Urbild \(x=\displaystyle\frac {y+1}{2}\) verschaffen.

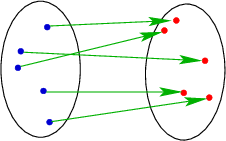
inj_surj

Eine weder injektive noch surjektive Abbildung:

Sei \(M\) die Menge aller Menschen die je gelebt haben. \(f:M\to M\) ordnet jedem Menschen seine Mutter zu.

  • nicht injektiv (Geschwister haben dieselbe Mutter)

  • nicht surjektiv (Männer sind niemals Mütter)

notinj_notsurj

Die Umkehrfunktion

Ist die Abbildung \(f:M\to N\) bijektiv, dann besitzt jedes \(n\in N\) genau ein Urbild.

Man findet daher zu jedem \(n\in N\) ein eindeutiges \(m\in M\) mit \(f(m)= n\) .

Definition:
Die Abbildung \(f^{-1}:N\to M\), die jedem \(n\in N\) sein Urbild zuordnet, heißt Umkehrfunktion von \(f\).

Beispiel: Matrikelnummern
Hier sind \(M\) die Menge der Erstsemester und \(N\) die Menge aller Matrikelnummern von Erstsemestern. Dann kann man die Zuordnungsvorschrift umkehren:

\(\begin{array}{rcl}f:M&\to&N\\
\text{Person}&\mapsto&\text{Matrikelnummer}\\f^{-1}:N&\to&M\\
\text{Matrikelnummer}&\mapsto&\text{Person}\end{array}\)

Beispiel: Lineare Funktion
\(h:\mathbb{R}\to \mathbb{R}\) mit \(h(x)=2x+3\) hat die Umkehrfunktion \(h^{-1}\colon\mathbb {R}\to \mathbb {R}\) mit \(h^{-1}( y) = \displaystyle\frac {1}{2}(y-3)\), denn:

\(\begin{array}{rcl}y=2x+3\Leftrightarrow y-3&=&2x\\&&\\ \Leftrightarrow\;\;\displaystyle\frac{1}{2}(y-3)&=&x\end{array}\)

Modifié le: mardi 22 janvier 2019, 19:17