1.6c Funktionen (Fortsetzung)
1.6 Funktionen (Fortsetzung)
Verkettung von Funktionen
Oft wendet man mehrere Funktionen nacheinander an. Wenn man zuerst die Funktion \(f\) und dann die Funktion \(g\) anwendet, also \( g(f(x)) \) bestimmt, dann schreibt man dafür
\( (g \circ f)(x) \)
Für manche Studierende ist diese Notation etwas gewöhnungsbedürftig, da die Funktionen hier von rechts nach links in Aktion treten, aber vielleicht hilft es etwas, wenn man sich die Sprechweise "g nach f" angewöhnt.
Mit Hilfe eines kleinen Bildchens kann man auch eine andere typische Fehlerquelle einsehen: Wenn \(f\) und \(g\) beide bijektive Funktionen sind mit Umkehrfunktionen \( f^{-1}\) und \(g^{-1}\), dann ist auch \( g\circ f\) eine invertierbare Funktion mit
\( (g\circ f)^{-1}=f^{-1}\circ g^{-1}.\)
Während man bei \( g\circ f\) zuerst \(f\) und dann \(g\) anwendet, muss man auf dem "‘Rückweg"’ zuerst \( g^{-1} \) und dann erst \( f^{-1} \) benutzen.
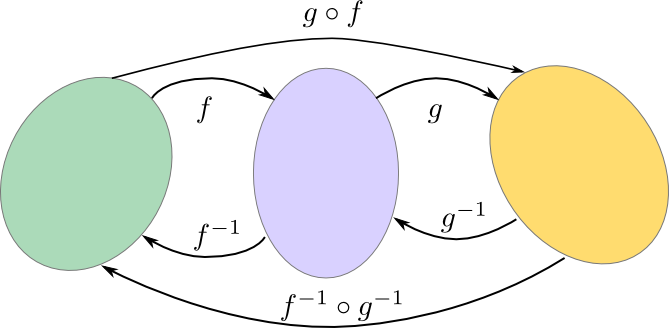
Reelle Funktionen
Die Abbildungen, mit denen wir am meisten zu tun haben werden, sind reelle Funktionen, also Abbildungen \(f: D \to \mathbb{R} \), wobei der Definitionsbereich \( D\) eine Teilmenge von \(\mathbb{R}\) ist (oft ganz \(\mathbb {R} \).
Der Graph (oder das Schaubild)\(G_f\) der reellen Funktion \( f \) ist die Menge
\( G_f:=\{(x,f( x));\;x\in D\}\subset\mathbb{R}\times\mathbb{R} \,.\)
Eine Funktion \( f: \to \mathbb {R} \) heißt periodisch mit der Periode \( p > 0 \), wenn
\( f( x+p)=f( x) \)
für alle \ x \in \mathbb{R} \) .
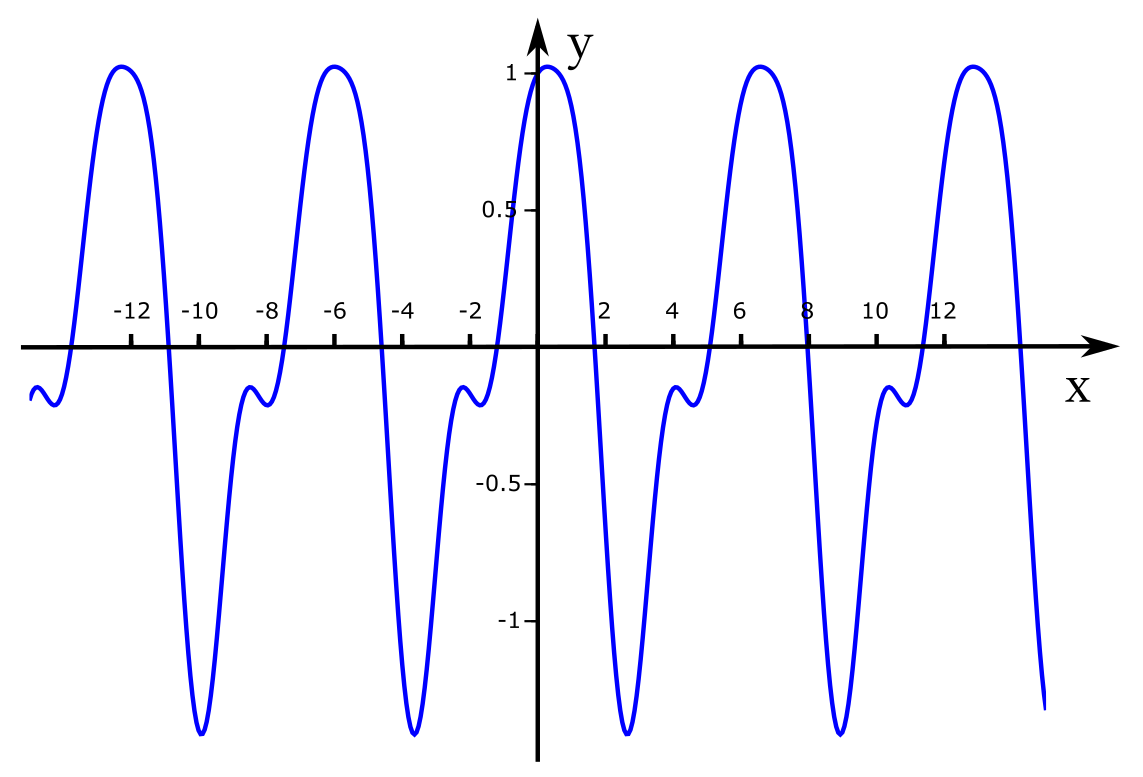
Typischerweise interessiert man sich für die minimale Periode \( p > 0\), die eine Funktion gegebenenfalls besitzt.
Die wichtigsten Beispiel für periodische Funktionen sind die trigonometrischen Funktionen Sinus und Cosinus, die wir in einem späteren Kapitel ausführlich behandeln.
Sei \( f: D \to \mathbb{R}\) eine reelle Funktion mit \( x \in D \Leftrightarrow -x \in D\):
Dann heißt eine Funktion gerade, falls \( f( x) = f(-x)\) für alle \( x\in D \) und ungerade, falls \( f( x) = -f(-x)\) für alle \(x\in D\).
G raphen von geraden Funktion sind spiegelsymetrisch bezüglich der y-Achse. Graphen ungerader Funktionen sind punktsymetrisch bezüglich des Ursprungs.
Ohne Test und Feedback weiter zu Kapitel 2: Vektoren
