1.6b Funktionen (Fortsetzung)
1.6 Funktionen (Fortsetzung)
Injektivität und Surjektivität
-
surjektiv, falls es zu jedem Element \(y\) von \(N\) mindestens ein \(x\in M\) gibt mit \(f( x)=y\).
-
injektiv, falls es zu jedem Element \(y\) von \(N\) höchstens ein \(x\in M\) gibt mit \(f( x)=y\).
-
bijektiv, falls \(f\) injektiv und surjektiv ist, d.h. falls es zu jedem Element \(y\) von \(N\) genau ein \(x\in M\) gibt mit \(f( x)=y\).
-
\(f:M\to N\) ist surjektiv genau dann, wenn \(f(M)=N\) ist.
-
\(f:M\to N\) ist injektiv, wenn kein Element von \(N\) zwei verschiedene Urbilder besitzt, falls also
\(a\neq b\Rightarrow f(a)\neq f(b)\) für alle \(a,b\in M.\)
In Worten ausgedrückt heißt das, dass verschiedene Argumente auch verschiedene Funktionswerte liefern. Um Injektivität nachzuprüfen benutzt man gelegentlich die Umkehrung dieser Aussage: \(f\) ist genau dann injektiv, wenn für beliebige \(a,b \in M\)
\(f(a)=f(b)\Rightarrow a=b\)
gilt.
Beispiele
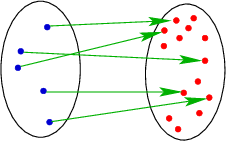
Injektive, aber nicht surjektive Abbildungen:
Sei \(M\) die Menge aller Studierenden der Ruhr-Uni. Die Abbildung \(f:M\to \mathbb {N}\) ordnet jedem Studierenden seine Matrikelnummer zu.
-
injektiv, denn keine zwei Studierende haben dieselbe Matrikelnummer
-
nicht surjektiv, denn nicht alle (natürlichen) Zahlen kommen als Matrikelnummer vor.
Schematisch dargestellt:
Surjektive, aber nicht injektive Abbildungen:
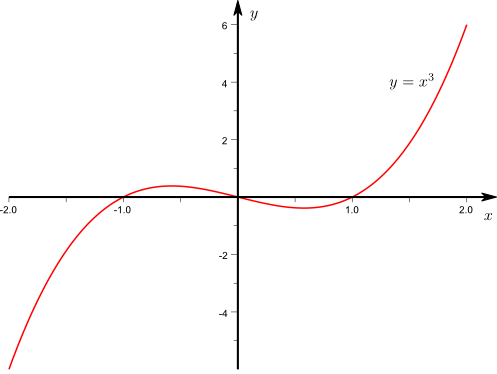
Die Abbildung \(k:\mathbb{R}\to \mathbb {R}\) mit \(q(x)=x^3-x\) ist
-
nicht injektiv , denn \(q(-1)=q(0)=q(1)=0\)
-
surjektiv , denn wenn man das Schaubild von \(q\) betrachtet, erkennt man, dass alle reellen Zahlen als Funktionwerte vorkommen
Schematisch:
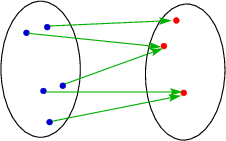
Bijektive Abbildung:
Die Abbildung \(f:\mathbb {R}\to\mathbb{R}\), die jeder reellen Zahl \(x\) die Zahl \(f(x)=2x-1\) zuordnet ist
- injektiv und surjektiv
denn zu \(f(x)=y\) kann man sich auf eindeutige Weise das Urbild \(x=\displaystyle\frac {y+1}{2}\) verschaffen.
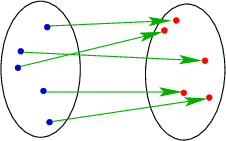
Eine weder injektive noch surjektive Abbildung:
Sei \(M\) die Menge aller Menschen die je gelebt haben. \(f:M\to M\) ordnet jedem Menschen seine Mutter zu.
-
nicht injektiv (Geschwister haben dieselbe Mutter)
-
nicht surjektiv (Männer sind niemals Mütter)
Die Umkehrfunktion
Ist die Abbildung \(f:M\to N\) bijektiv, dann besitzt jedes \(n\in N\) genau ein Urbild.
Man findet daher zu jedem \(n\in N\) ein eindeutiges \(m\in M\) mit \(f(m)= n\) .
Beispiel: Matrikelnummern
Hier sind \(M\) die Menge der Erstsemester und \(N\) die Menge aller Matrikelnummern von Erstsemestern. Dann kann man die Zuordnungsvorschrift umkehren:
\(\begin{array}{rcl}f:M&\to&N\\
\text{Person}&\mapsto&\text{Matrikelnummer}\\f^{-1}:N&\to&M\\
\text{Matrikelnummer}&\mapsto&\text{Person}\end{array}\)
Beispiel: Lineare Funktion
\(h:\mathbb{R}\to \mathbb{R}\) mit \(h(x)=2x+3\) hat die Umkehrfunktion \(h^{-1}\colon\mathbb {R}\to \mathbb {R}\) mit \(h^{-1}( y) = \displaystyle\frac {1}{2}(y-3)\), denn:
\(\begin{array}{rcl}y=2x+3\Leftrightarrow y-3&=&2x\\&&\\ \Leftrightarrow\;\;\displaystyle\frac{1}{2}(y-3)&=&x\end{array}\)
