2.1a Vektoren (Fortsetzung)
2.1 Vektoren (Fortsetzung)
Rechnen mit Vektoren
Für Vektoren gibt es zunächst einmal zwei Rechenoperationen: Die Addition von Vektoren und die skalare Multiplikation (Skalierung) von Vektoren, die man nicht mit dem später noch auftretenden Skalarprodukt zwischen zwei Vektoren verwechseln sollte.
Die Hintereinanderausführung von zwei Parallelverschiebungen \(\overrightarrow {PQ}\) und \(\overrightarrow{QR}\) ergibt wieder eine Parallelverschiebung, nämlich \(\overrightarrow{PR}\), denn der Punkt P wird ja zunächst nach Q und von Q aus nach R verschoben, insgesamt also von P nach R.
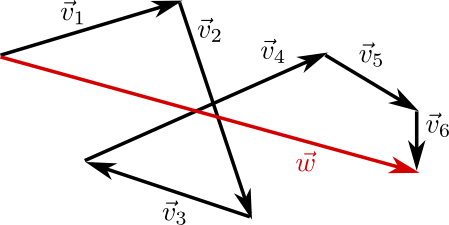
Geometrisch kann man sich das sehr anschaulich klarmachen, indem man die entsprechenden Vektorpfeile aneinandersetzt.
Unter einem Fachwerk versteht man ein Tragwerk aus geraden, masselosen Stäben, bei denen jeder Stab an zwei Knoten gelenkig mit anderen Stäben verbunden ist, z.B. bei Brücken, Kränen oder Strommasten.
An den Knoten können äußere Kräfte angreifen, außerdem sind eventuell einer oder mehrere der Knoten fest oder verschiebbar gelagert.
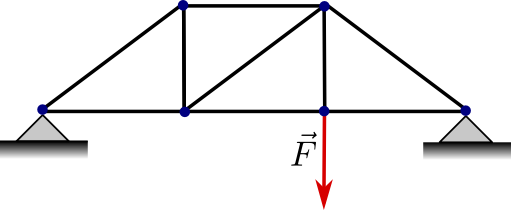
In der Technischen Mechanik bestimmt man die auftretenden Kräfte durch Gleichgewichtsbedingungen, d.h. an jedem einzelnen Knoten muss die vektorielle Addition der dort angreifenden Kräfte \(\vec{0}\) ergeben.
Dies führt dann auf ein Lineares Gleichungssystem, wie wir es in Kapitel 4 behandeln.
Für die Vektoraddition gelten ähnliche Rechenregeln wie für die Addition von reellen Zahlen.
-
\(\;\; \vec{x}+\vec{y}=\vec{y}+\vec{x}\; \; \; \; \) (Kommutativität)
-
\(\;\; (\vec{x}+\vec{y})+ \vec{z}=\vec{x} +(\vec{y}+\vec{z})\; \; \; \; \) (Assoziativität)
-
\(\;\; \vec{x}+\vec{0}= \vec{0}+ \vec{x}=\vec{x}\), d.h. der Nullvektor ist das neutrale Element
-
\(\;\; \vec{x}+(-\vec{x})= \vec{0}\), d.h. \(-\vec{x}\; \; \) ist das inverse Element von \(\vec{x}\)
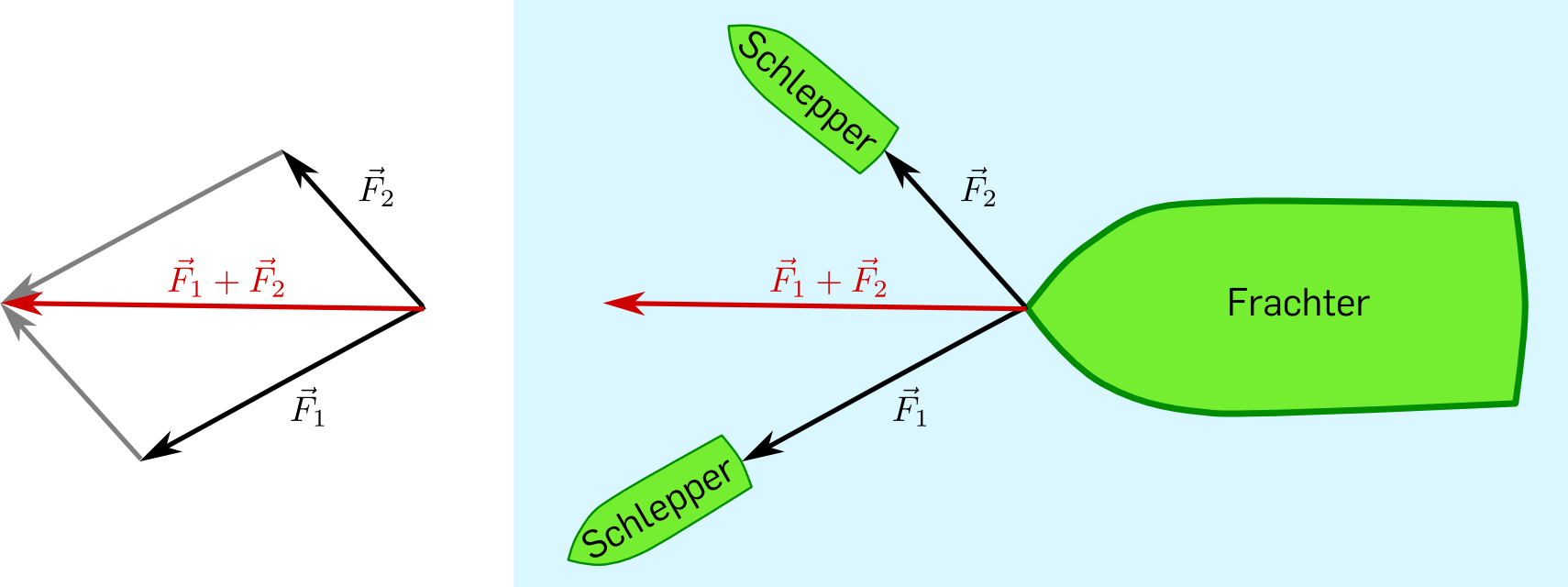
Vektoren kann man zum Addieren also einfach "Aneinanderhängen":
Darüber hinaus kann man Vektoren mit einem reellen Faktor skalieren. Der Vektor \(\alpha \vec{v}\) hat dieselbe Richtung wie \(\vec{v}\), aber die \(\alpha \)-fache Länge. Wenn \(\alpha <0\) ist, dann zeigen \(\vec{v}\) und \(\alpha \vec{v}\) in entgegengesetzte Richtungen.
Insbesondere erhält man für \(\alpha =-1\) den schon angesprochenen Vektor \(-\vec{v}=(-1)\vec{v}\), der dieselbe Länge wie \(\vec{v}\), aber die genau entgegengesetzte Richtung hat.
\(\begin{array}{rcl}\alpha\cdot(\beta\cdot\vec{x})&=&(\alpha\cdot\beta)\cdot\vec{x}\\1\cdot\vec{x}&=&\vec{x}\\\alpha\cdot(\vec{x}+\vec{y})&=&\alpha\cdot\vec{x}+\alpha\cdot\vec{y}\;\;\;\;\text{(Distributivgesetz)}\\ (\alpha+\beta)\cdot\vec{x}&=&\alpha\cdot\vec{x}+\beta\cdot\vec{x}\;\;\;\;\text{(Distributivgesetz)}\end{array}\)
In Koordinaten werden Vektoren komponentenweise addiert bzw. subtrahiert, es ist also
\(\vec{x}+\vec{y}=\left(\begin{array}{c}x_1\\x_2\\ \vdots\\x_n\end{array}\right)+\left(\begin{array}{c}y_1\\y_2\\{\vdots}\\y_n\end{array}\right)=\left(\begin{array}{c}x_1+y_1\\x_2+y_2\\{\vdots}\\x_n+y_n\end{array}\right)\)
Auch die Skalierung erfolgt komponentenweise, d.h. für eine beliebige Zahl \(\alpha \in \mathbb{R}\) gilt:
\(\alpha\cdot\vec{x}=\alpha\cdot\left(\begin{array}{c}x_1\\x_2\\{\vdots}\\x_n\end{array}\right)=\left(\begin{array}{c}\alpha x_1\\\alpha x_2\\{\vdots}\\\alpha x_n\end{array}\right).\)
\(3\left(\begin{array}{r} 2\\ -3\\ 1\end{array}\right) +\left(\begin{array}{r} 2\\ 5\\ 0 \end{array}\right) - \left(\begin{array}{r} -2\\ 1\\ 2\end{array}\right) = \left(\begin{array}{r} 10 \\ -5 \\ 1 \end{array}\right)\)
Einen weiteren Zusammenhang zwischen Punkten in der Ebene bzw. im Raum und Vektoren stellt die folgende Definition her.
Sei im \(\mathbb{R}^2\) oder \(\mathbb{R}^3\) ein kartesisches Koordinatensystem gegeben. Dann ist zu jedem Punkt P der Ortsvektor \(\vec{p}\) von P gegeben als
\(\vec{p}=\overrightarrow{OP}.\)
Insbesondere ist für zwei Punkte P und Q mit Ortsvektoren \(\vec{p}\) und \(\vec{q}\) immer \(\overrightarrow {PQ}=\vec{q}-\vec{p}\).
