2.1b Vektoren (Fortsetzung)
2.1 Vektoren (Fortsetzung)
Bevor wir uns der Beschreibung von Geraden und Ebenen durch Vektoren zuwenden, benötigen wir noch ein Kriterium, um zu überprüfen, ob mehrere vorgegebene Vektoren alle in "verschiedene" Richtungen zeigen, oder ob beispielsweise ein Vektor in der Ebene enthalten ist, die durch zwei andere Vektoren festgelegt wird.
Lineare Unabhängigkeit
Durch die Vektoraddition und Skalierung kann man aus zwei Vektoren \(\vec{p},\vec{q}\in \mathbb {R}^ n\) viele weitere Vektoren konstruieren:
\(\vec{x}=\lambda\vec{p}+\mu\vec{q}\)
mit beliebigen Skalierungsfaktoren \(\lambda , \mu \in \mathbb {R}\). Jede solche Darstellung nennt man eine Linearkombination von \(\vec{p}\) und \(\vec{q}\). Geometrisch sind die Linearkombinationen von \(\vec{p}\) und \(\vec{q}\) die Ortsvektoren aller Punkte, die in einer Ebene liegen. Auf diesen Punkt kommen wir später genauer zurück.
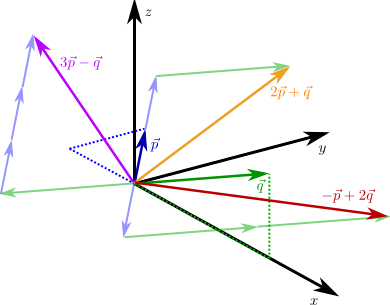
Für die beiden Vektoren \(\vec{p}=\left(\begin{array}{c} -1 \\ 1 \\ 0\end{array}\right)\) und \(\vec{p}=\left(\begin{array}{c} 2 \\ 0 \\ 1\end{array}\right)\) im \(\mathbb {R}^3\) sind einige Linearkombinationen von \(\vec{p}\) und \(\vec{q}\) eingezeichnet.
\(\lambda_1\vec{p}_1+\lambda_2\vec{p}_2+\dots+\lambda_k\vec{p}_k=\vec{0}\)
nur die Lösung \(\lambda_1=\lambda_2=\dots =\lambda_k=0\) besitzt. Im Gegensatz dazu sind die Vektoren \(\vec{p}_1\), \(\vec{p}_2,\dots ,\vec{p}_ k\) linear abhängig, falls man Zahlen \(\lambda_1,\lambda_2,\dots ,\lambda_k\) findet, die nicht alle verschwinden, so dass\(\lambda_1\vec{p}_1+\lambda_2\vec{p}_2+\dots+\lambda_k\vec{p}_k=\vec{0}.\)
Im allgemeinen müssen wir ein lineares Gleichungssystem lösen (und dabei herausfinden, dass es nur die Lösung \(\lambda _1=\lambda _2=\dots =\lambda _ k=0\) gibt), um die lineare Unabhängigkeit von Vektoren zu überprüfen. Da wir ein allgemeines Lösungsverfahren erst in Kapitel 4 kennenlernen werden, stellen wir hier die wichtigsten Spezialfälle zusammen.
-
Wenn einer der k Vektoren \(\vec{p}_1, \vec{p}_2,\dots ,\vec{p}_ k\) der Nullvektor ist, zum Beispiel \(\vec{p}_1=\vec{0}\), dann sind die Vektoren automatisch linear abhängig, denn man kann die Vektorgleichung mit \(\lambda _1\) beliebig und \(\lambda _2=\lambda _3=\dots =\lambda _ k=0\) lösen.
-
Zwei Vektoren \(\vec{p}\neq \vec{0}\) und \(\vec{q}\neq \vec{0}\) sind linear unabhängig, wenn \(\vec{q}\) kein Vielfaches von \(\vec{p}\) ist, d.h. wenn es kein \(\lambda \in \mathbb {R}\) gibt, so dass \(\)\vec{q}=\lambda \vec{p}\(\).
-
Drei Vektoren \(\vec{p},\vec{q},\vec{r}\neq \vec{0}\) sind linear unabhängig, wenn \(\vec{q}\) kein Vielfaches von \(\vec{p}\) und \(\vec{r}\) keine Linearkombination von \(\vec{p}\) und \(\)\vec{q}\(\) sind.
Im \(\mathbb {R}^2\) kann man jeden Vektor als Linearkombination der beiden Vektoren
\(\vec{e}_1=\left(\!\begin{array}{c}1\\0\end{array}\!\right)\) und \(\vec{e}_2=\left(\!\begin{array}{c}0\\1\end{array}\!\right)\)
darstellen, denn
\(\vec{x}=\left(\begin{array}{c}x_1\\x_2\end{array}\right)=x_1\left(\begin{array}{c}1\\0\end{array}\right)+x_2\left(\begin{array}{c}0\\1\end{array}\right)\)
Man könnte aber auch statt \(\vec{e}_1\) und \(\vec{e}_2\) zwei andere Vektoren verwenden, zum Beispiel
\(\vec{b}_1=\left(\!\begin{array}{c}1\\1\end{array}\!\right)\) und \( \vec{b}_2=\left(\!\begin{array}{c}0\\2\end{array}\!\right)\)
Dann wäre
\(\vec{x}=\left(\begin{array}{c}x_1\\x_2\end{array}\right)=x_1\left(\begin{array}{c}1\\1\end{array}\right)+\frac{x_2-x_1}{2}\left(\begin{array}{c}0\\2\end{array}\right)\)
immer noch eindeutig als eine (andere!) Linearkombination dieser Vektoren \(\vec{b}_1\) und \(\vec{b}_2\) darstellbar. Diese Wahlmöglichkeit liegt der folgenden Definition zugrunde.
Jede Basis des \(\mathbb {R}^n\) besteht aus genau \(n\) Vektoren.
Wenn \(\{ \vec{b}_1,\vec{b}_2,\dots ,\vec{b}_ n \} \) eine Basis des \(\mathbb{R}^n\) ist, dann ist für jeden Vektor \(\vec{x}\in \mathbb {R}^ n\) die Darstellung
\(\vec{x}=\lambda_1\vec{b}_1+\lambda_2\vec{b}_2+\dots+\lambda_n\vec{b}_n\)
als Linearkombination der Basisvektoren eindeutig.
(Teil-)Beweis: Wir zeigen nur, dass die Darstellung jedes Vektors \(\vec{x}\) eindeutig ist. Falls nämlich
\(\vec{x}=\lambda_1\vec{b}_1+\lambda_2\vec{b}_2+\dots+\lambda_n\vec{b}_n=\mu_1\vec{b}_1+\mu_2\vec{b}_2+\dots+\mu_n\vec{b}_n\)
zwei Linearkombinationen sind, die den Vektor \(\vec{x}\) ergeben, dann erhält man durch Subtraktion der rechten Seite
\((\lambda_1-\mu_1)\vec{b}_1+(\lambda_2-\mu_2)\vec{b}_2+\dots+(\lambda_n-\mu_n)\vec{b}_n=\vec{0}\)
und weil die (Basis-)Vektoren \(\vec{b}_1,\vec{b}_2,\dots ,\vec{b}_ n\) linear unabhängig sind, müssen alle Koeffizienten verschwinden:
\(\lambda_1-\mu_1=\lambda_2-\mu_2=\dots=\lambda_n-\mu_n=0\)
und die "zwei" Linearkombinationen sind in Wahrheit ein und dieselbe Darstellung. Es gibt also nur eine einzige solche Darstellung von \(\vec{x}\).
\(\diamondsuit\)
-
Hat man zu wenige Vektoren, also weniger als n linear unabhängige Vektoren, dann zeigen diese insgesamt in zu wenige Richtungen und es lassen sich nicht alle Vektoren des \(\mathbb{R}^n\) durch Linearkombinationen darstellen.
-
Hat man zu viele Vektoren, also insgesamt mehr als n Vektoren, dann können diese nicht linear unabhängig sein.
\(\vec{e}_1=\left(\begin{array}{c}1\\0\\0\\{\vdots}\\0\end{array}\right),\vec{e}_2=\left(\begin{array}{c}0\\1\\0\\{\vdots}\\0\end{array}\right),\dots,\vec{e}_n=\left(\begin{array}{c}0\\0\\0\\{\vdots}\\1\end{array}\right)\)
eine Basis, die sogenannte Standardbasis. Die Vektoren \(\vec{e}_1,\vec{e}_2,\ldots , \vec{e}_n\) nennt man auch die Standardeinheitsvektoren.Im nächsten Abschnitt sehen wir, dass die Standardeinheitsvektoren nicht nur eine Basis bilden, sondern weitere günstige Eigenschaften besitzen.
