1 - Pre Learning (Buch)
Quadratische Funktionen
Definition 1.11
Seien $a,b,c \in \mathbb{R}$ und $a \not=0$. Eine Funktion $f: \mathbb{R} \to \mathbb{R}$ darstellbar durch $f(x)=ax^2 +bx + c$ heißt quadratische Funktion.
Wenn wir über eine Wertetabelle für mehrere Punkte aus dem
Definitionsbereich die Paare $(x,f(x))$ bestimmen und diese in das
Koordinatensystem übertragen, erhalten wir als Graphen eine sogenannte
Parabel. Die $y$-Achse enthält alle Werte $(0,y)$. Diese Parabel
schneidet daher die $y$-Achse im Punkt $(0,c)$, denn
$f(0)=a \cdot 0^2 + b \cdot 0 + c=c$. Wir nennen auch hier, wie bei
linearen Gleichungen, $c$ den $y$-Achsenabschnitt.
Ob eine Parabel nach oben oder nach unten geöffnet ist, wird durch den
Vorfaktor $a$ festgelegt: Ist $a>0$, dann ist die Parabel nach oben, ist
$a<0$, dann ist die Parabel nach unten geöffnet.
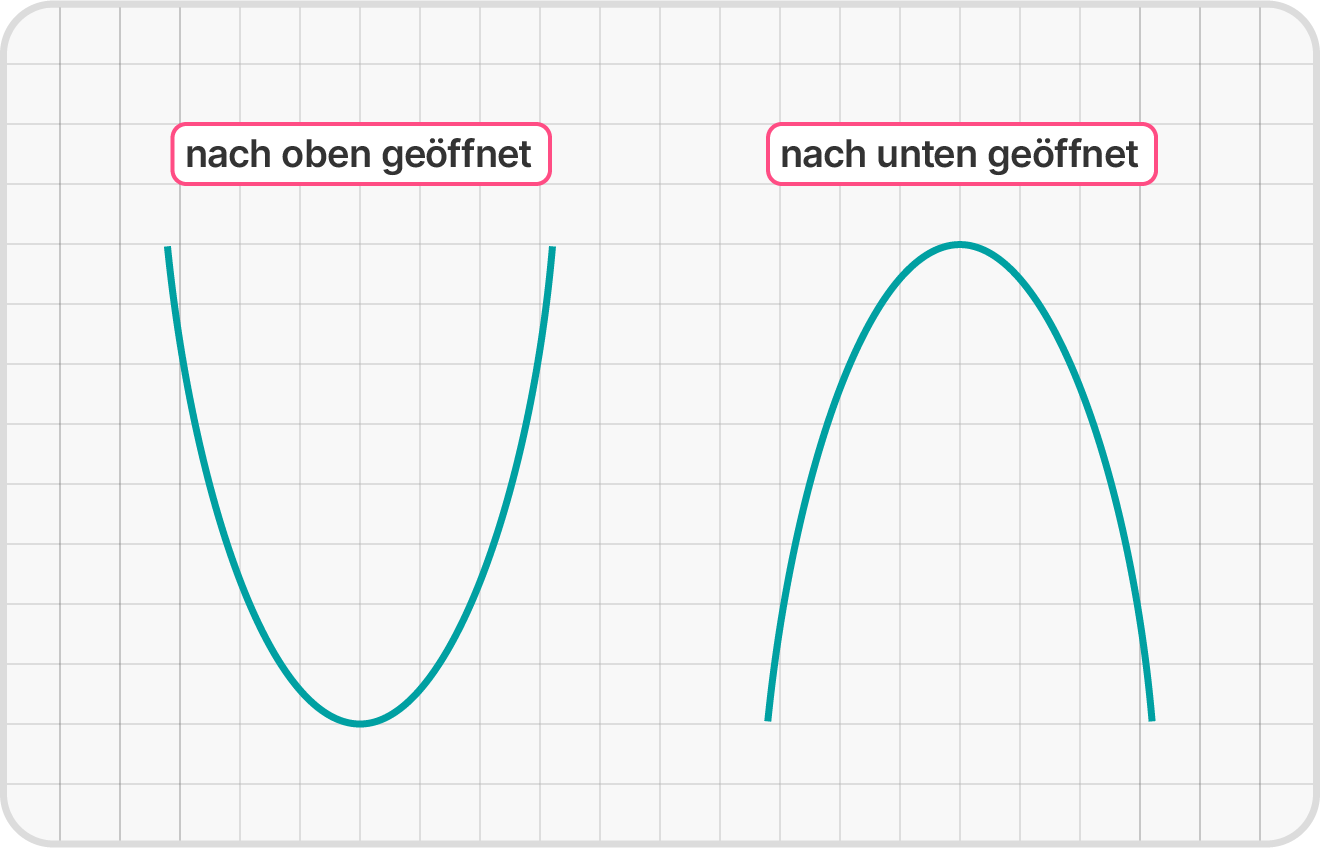
Um die Position einer Parabel im Koordinatensystem eindeutig festzulegen, berechnen wir den Scheitelpunkt der Parabel. Dieser ist der kleinste bzw. der größte Funktionswert der quadratischen Funktion.
Wir wollen uns zuerst ansehen, wie wir den Scheitelpunkt einer Parabel
für einfache Fälle von quadratischen Funktionen bestimmen können:
Fall 1) $f(x)=x^2$. Der Graph ist die sogenannte Normalparabel (Es gilt: $a=1$, $b=0$ und $c=0$). Wir haben sie bereits früher in dieser Lerneinheit visualisiert, siehe Graphen von Funktionen. Wenn wir reelle Zahlen quadrieren, dann ist das Ergebnis stets größer oder gleich null. Quadrieren wir eine von null verschiedene Zahl, so ist das Ergebnis größer null. Der kleinste Wert dieser quadratischen Funktion wird daher in $x=0$ erreicht. Der Scheitelpunkt hat damit die Koordinaten $S=(0,f(0))=(0,0)$.
Fall 2) $f(x)=ax^2$. Diese Funktion unterscheidet sich vom Fall 1) durch den Vorfaktor $a$, den Streckungsfaktor. Dieser Vorfaktor vergrößert, verkleinert oder ändert das Vorzeichen aller unserer Funktionswerte und verändert so die Form unserer Parabel. Er ändert aber nichts an der Position und den Koordinaten des Scheitelpunktes.
Achtung!
Durch den Streckungsfaktor bleibt der Scheitelpunkt erhalten, aber die Parabel wird gestreckt oder bestaucht.
Beim Zeichnen gehen wir wie folgt vor:
Wir tragen den Scheitelpunkt ins Koordinatensystem ein. Dann gehen wir von diesem jeweils einen $1$-Schritt in $x$-Richtung nach rechts und links. Und dann gehen wir in $y$-Richtung jeweils einen Schritt mit dem Wert $a$. Dieser Schritt geht nach oben oder unten, in Abhängigkeit von dem Vorzeichen von $a$. Durch diese beiden neuen Koordinatenpunkte und den Scheitelpunkt verläuft die Parabel.
Fall 3) $f(x)=x^2+d$. Der Summand $d$ ändert die Position der Parabel entlang der $y$-Achse Durch Veränderung von $d$ verschiebt sich die Parabel nach oben oder unten. Der $x$-Wert des Scheitelpunkts bleibt konstant. Der Funktionswert verändert sich in Abhängigkeit von $d$. Die Koordinaten des Scheitelpunkts sind damit $S=(0,f(0))=(0,d).$
Fall 4) $f(x)=(x+s)^2$. Hier betrachten wir eine andere Darstellung einer quadratischen Funktion. Der Summand $s$ im quadratischen Term ändert
die Position der Parabel entlang der $x$-Achse. Durch Veränderung von
$s$ verschiebt sich die Parabel nach links oder rechts um $s$, wobei ein
positives $s$ eine Verschiebung nach links und ein negatives $s$ eine
Verschiebung nach rechts bewirkt. Der Funktionswert des Scheitelpunkts
bleibt dabei konstant. Die Koordinaten des Scheitelpunkts sind damit
$S=(-s,0)$.
Nun wollen wir den allgemeinen Fall einer quadratischen Funktion betrachten. Ihren Scheitelpunkt können wir mithilfe der quadratischen Ergänzung berechnen.
Erinnern Sie sich noch, wie das Verfahren quadratische Ergänzung funktioniert? Falls nicht, so finden Sie eine kurze Wiederholung dieses Themas im Anhang.
Wir können eine quadratische Funktion $f(x)$ wie folgt umformen: $$f(x)=ax^2+bx+c = a(x+\frac{b}{2a})^2 - \frac{b^2}{4a} + c$$ Mit den Erkenntnissen aus der Fallunterscheidung 1-4 folgern wir, dass der Scheitelpunkt bei $S=(-s,d)=(-\frac{b}{2a}, - \frac{b^2}{4a} + c)$ liegt. Die Darstellung $f(x)=(x+s)^2+d$ nennen wir auch die Scheitelpunktform.
