1 - Pre Learning (Buch)
| Website: | RUB Moodle |
| Kurs: | eTutoring-KB |
| Buch: | 1 - Pre Learning (Buch) |
| Gedruckt von: | Gast |
| Datum: | Montag, 5. Januar 2026, 04:13 |
Inhaltsverzeichnis
- 1. Einleitung
- 2. Definition einer Abbildung
- 3. Urbilder von Mengen
- 4. Injektive, surjektive und bijektive Abbildungen
- 5. Umkehrbare Abbildungen
- 6. Graphen von Abbildungen
- 7. Lineare Funktionen
- 8. Quadratische Funktionen
- 9. Anhang
- 10. Anhang: Äquivalenzumformungen
- 11. Anhang: Lösungen linearer Gleichungen
- 12. Anhang: Lösungen quadratischer Gleichungen
Pre Learning 1
Sie finden hier ein digitales Buch vor sich. Es enthält Seiten zum Weiterblättern aber gleichzeitig viele interaktive Aufgaben, mit denen Sie direkt überprüfen können, ob Sie das gerade Gelesene verstanden haben und anwenden können.
Das digitale Material in diesem Buch wurde im Rahmen des Projekts VORsprung, eines digitalen Vorbereitungskurses für internationale Studierende und ist urheberrechtlich geschützt.
Es kann innerhalb dieses Moodle-Kurses genutzt werden, darf aber nicht extern gespeichert werden.
Definition einer Abbildung
Definition 1.1
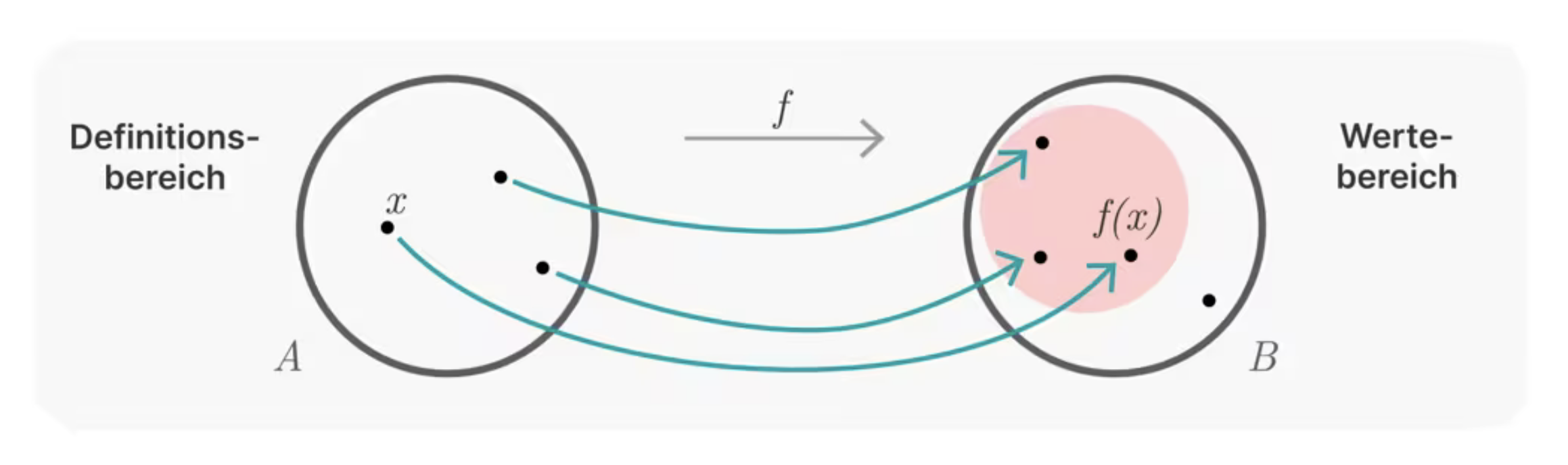
Seien $A$ und $B$ Mengen. Unter einer Abbildung von $A$ nach $B$ verstehen wir eine Zuordnung $f$, die jedem Element $x \in A$ genau ein Element aus $B$ zuordnet, welches wir als $f(x)$ bezeichnen. Wir schreiben $$f:A \to B \qquad \mbox{bzw.} \qquad x \mapsto f(x)$$
Die Menge $A$, mit der wir beginnen, heißt Definitionsbereich. Die Menge $B$, in die die Abbildung führt, heißt Wertebereich. Die Menge $\{ f(x) \;|\; x \in A \} \subseteq B$ wird mit $f(A)$ bezeichnet und heißt das Bild oder die Bildmenge von $A$ in $B$.
Hinweis
Beachten Sie die unterschiedlichen Pfeile, die in der Definition für Zuordnungen genutzt werden:
-
$f:A \to B$, bei der Zuordnung zwischen Mengen nutzen wir „ $\to$ “.
-
$x \mapsto f(x)$, bei der Zuordnung zwischen einzelnen Elementen nutzen wir „ $\mapsto$ “.
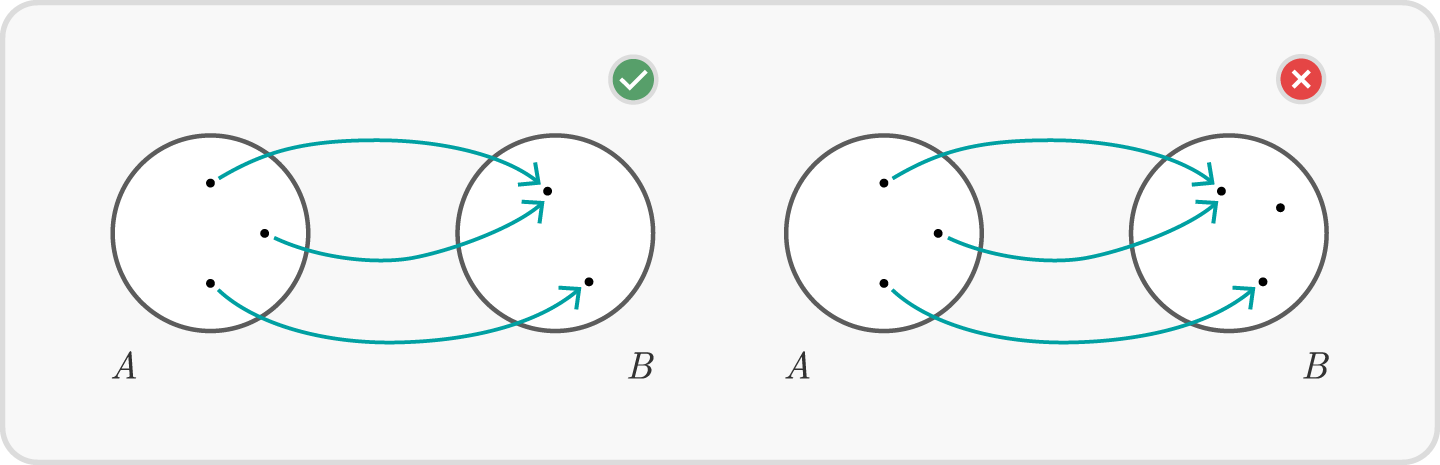
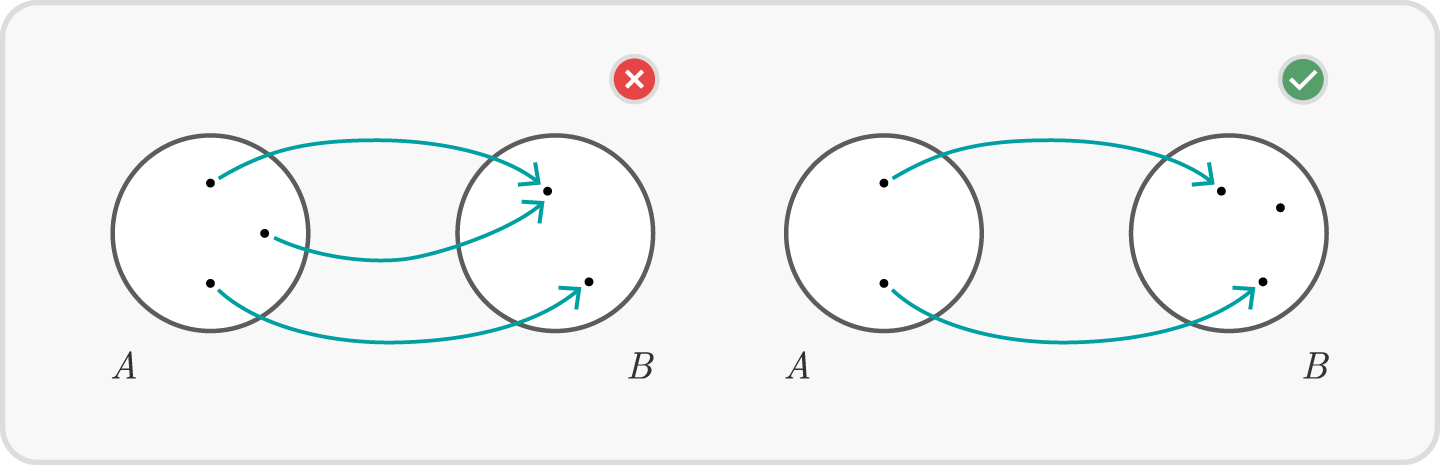
Welche der folgenden Zuordnungen sind Abbildungen?
(Die Lösung steht zum Aufklappen unter den Graphiken)
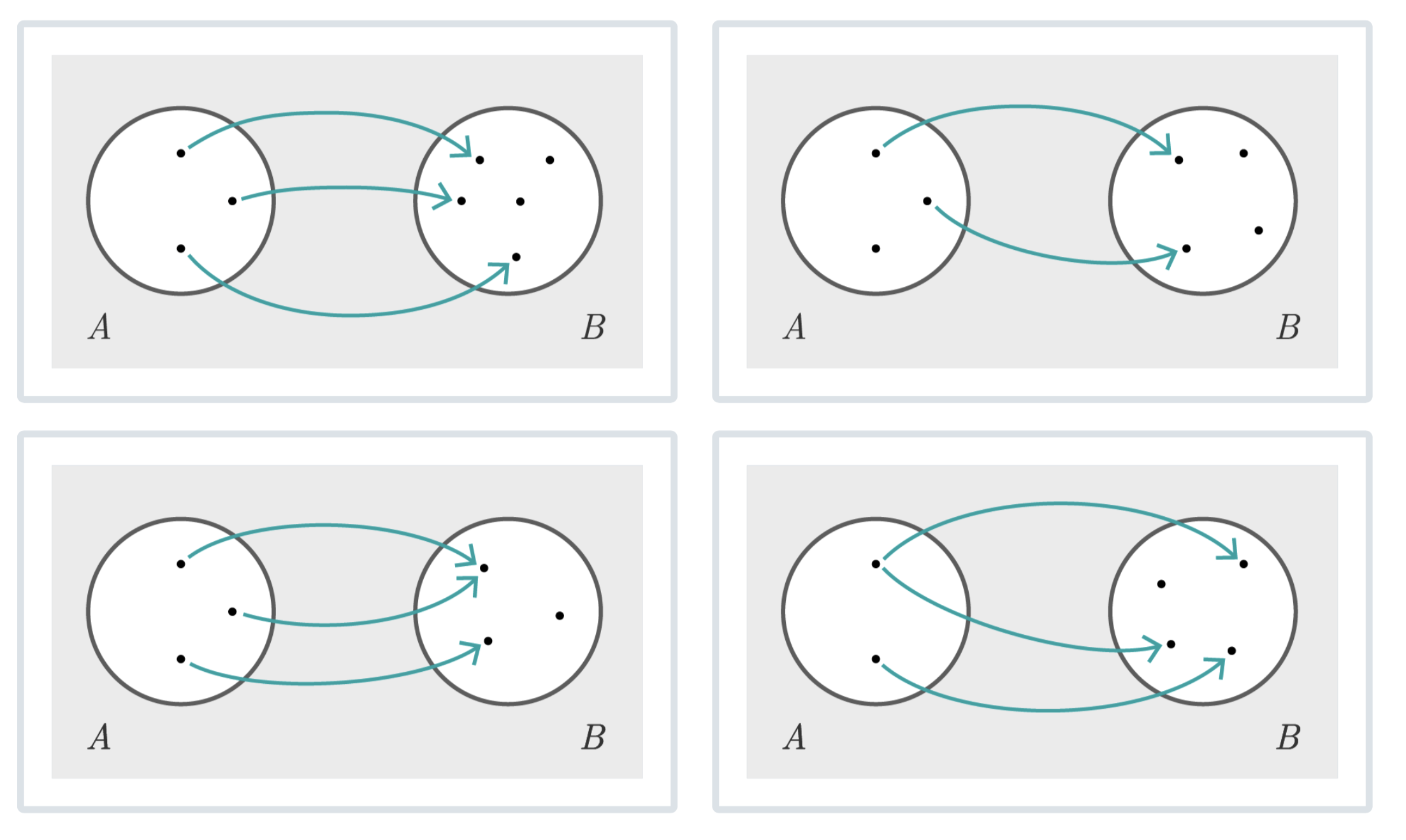
Lösung zum Aufklappen
Die Zuordnung rechts oben ist keine Abbildung, denn nicht in allen Punkten des Definitionsbereiches beginnt ein Pfeil. Die Zuordnung rechts unten ist ebenfalls keine Abbildung, denn die Zuordnung ist nicht eindeutig.
Beispiel
Es ist erlaubt, dass der Definitions- und der Wertebereich von
Zuordnungen die gleiche Menge ist.
Wir überprüfen jetzt für ein Beispiel einer Zuordnung der
natürlichen Zahlen $\mathbb{N}$ zu den natürlichen Zahlen, ob es
sich um eine Abbildung handelt. Die Zuordnung, die wir betrachten,
bildet natürliche Zahlen auf ihr Quadrat ab, d.h.
$$\mathbb{N} \to \mathbb{N} \quad \text{mit} \quad n \mapsto n^2.$$
Ist diese Zuordnung eine Abbildung?
Wir müssen überprüfen, ob wir für jedes beliebige Element aus
$\mathbb{N}$ das Quadrat bilden können. Das ist der Fall. Das
Quadrat einer natürlichen Zahl ist wieder eine natürliche Zahl.
Wir müssen weiter überprüfen, ob die Zuordnung einer natürlichen
Zahl zu ihrem Quadrat eindeutig ist. Auch das ist der Fall.
Damit sind die beiden Eigenschaften aus der Definition überprüft.
Diese Zuordnung ist eine Abbildung.
Es ist erlaubt, dass nicht jeder Zahlenwert im Wertebereich
getroffen wird, also Bild eines Wertes aus dem Definitionsbereich
ist. Hier werden die Zahlen $2$ und $5$ zum Beispiel nicht
getroffen, da sie beide nicht das Quadrat einer natürlichen Zahl
sind.
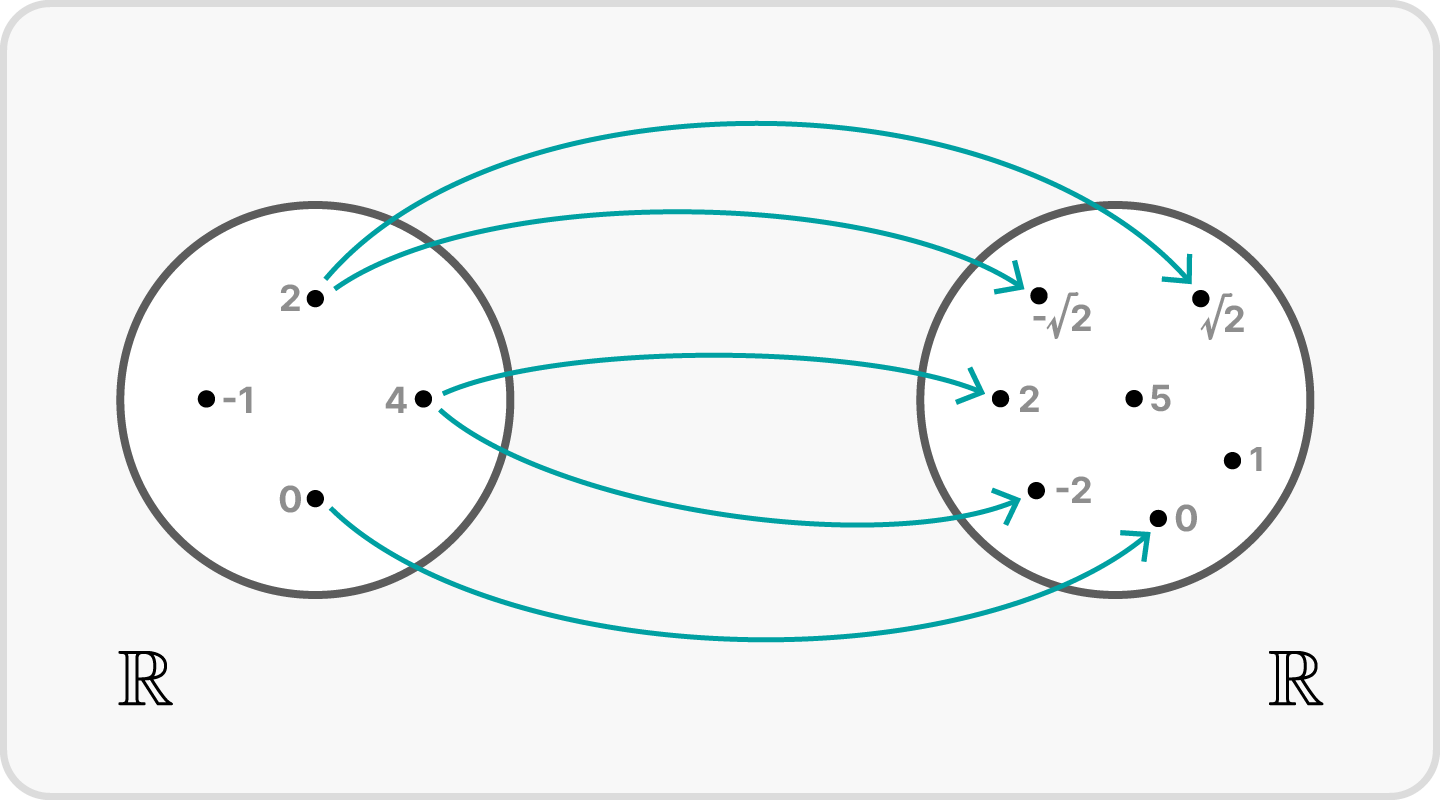
Beispiel
Wir betrachten als weiteres Beispiel die folgende Zuordnung der reellen Zahlen zu den reellen Zahlen: Einer Zahl $x$ wird ein $y$ zugeordnet, für das $y^2=x$ gilt. Diese Zuordnung ist keine Abbildung, denn für $x<0$ finden wir kein $y$ mit der vorgegebenen Eigenschaft und für jedes $x>0$ erhalten wir zwei Elemente, auf die wir $x$ abbilden.
Urbilder von Mengen
Definition 1.2
Sei $f : A \to B$ eine Abbildung und $b \in B$. Dann
ist das Urbild $$f^{-1}(b) = \{ a \in A \;|\; f(a) = b \}$$ von $b$
die Menge aller Elemente von $A$, die auf $b$ abgebildet werden.
Sei nun $C \subseteq B$. Dann heißt
$$f^{-1}(C) = \{ a \in A \;|\; f(a) \in C \}$$ das Urbild von
$C$. Es ist die Vereinigung aller $f^{-1}(c)$ mit $c \in C$.
Es gilt $f^{-1}(B) = A$, denn jedes Element von $A$ besitzt ein Bild in $B$.
Bemerkung
Wir sagen: $f^{-1}(C)$ ist das Urbild von $C$ unter $f$.
Beispiel
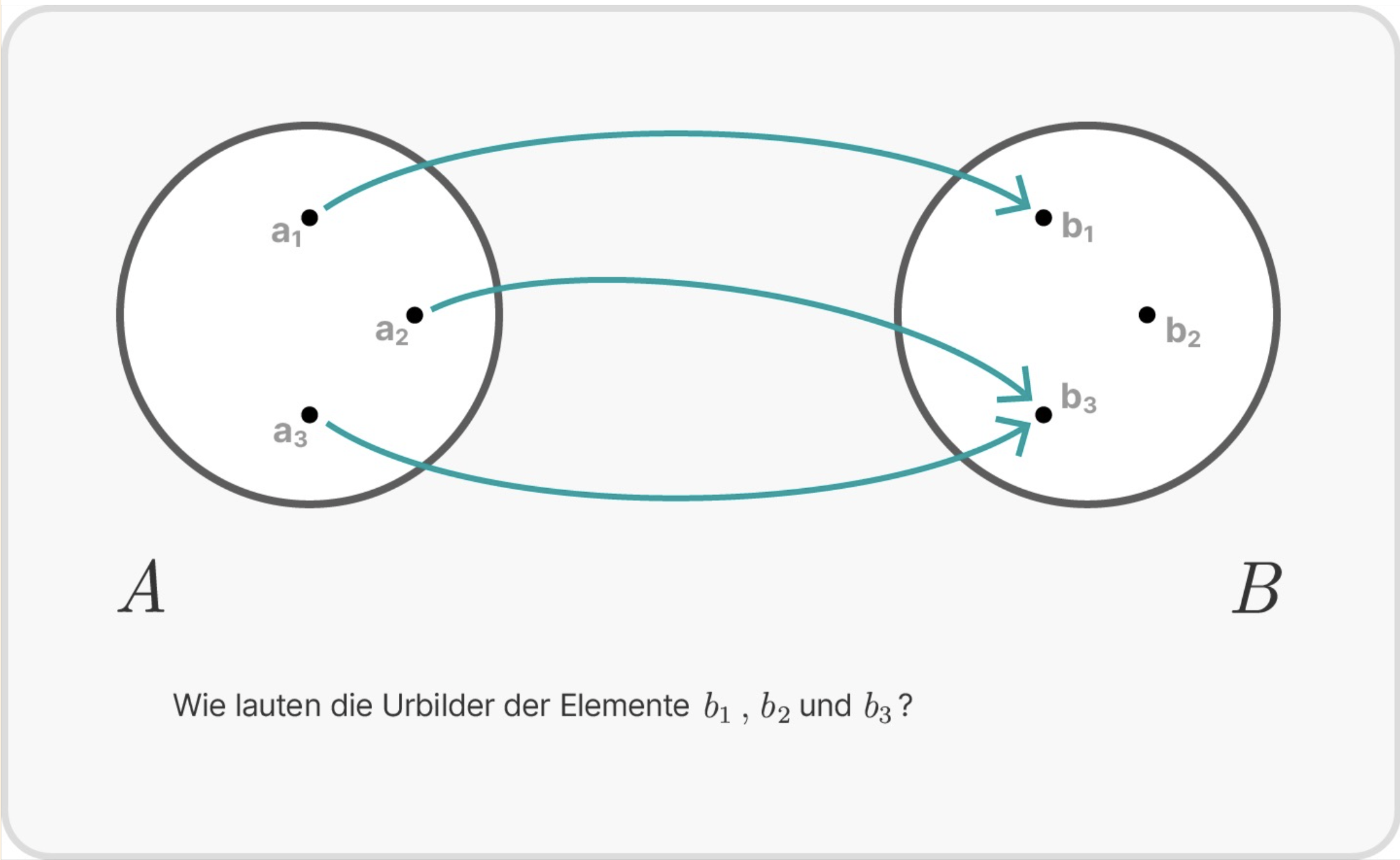
Lösung zum Aufklappen
Das Urbild von $b_1$ ist eine einelementige Menge und enthält nur das Element $a_1$. Wir schreiben_ $f^{-1}(b_1)=\{a_1\}$.
Das Urbild von $b_2$ ist leer. Wir schreiben_ $f^{-1}(b_2)=\{\}$.
Das Urbild von $b_3$ ist eine zweielementige Menge. Sie enthält die Elemente $a_2$ und $a_3$. Wir schreiben_ $f^{-1}(b_3)=\{a_2, a_3\}$.
Injektive, surjektive und bijektive Abbildungen
Wir kennen bereits die Eigenschaften, die eine Zuordnung haben muss, damit sie eine Abbildung zwischen zwei Mengen ist. In diesem Abschnitt werden wir zwei Eigenschaften von Abbildungen kennenlernen, über die wir spezielle Abbildungen charakterisieren können.
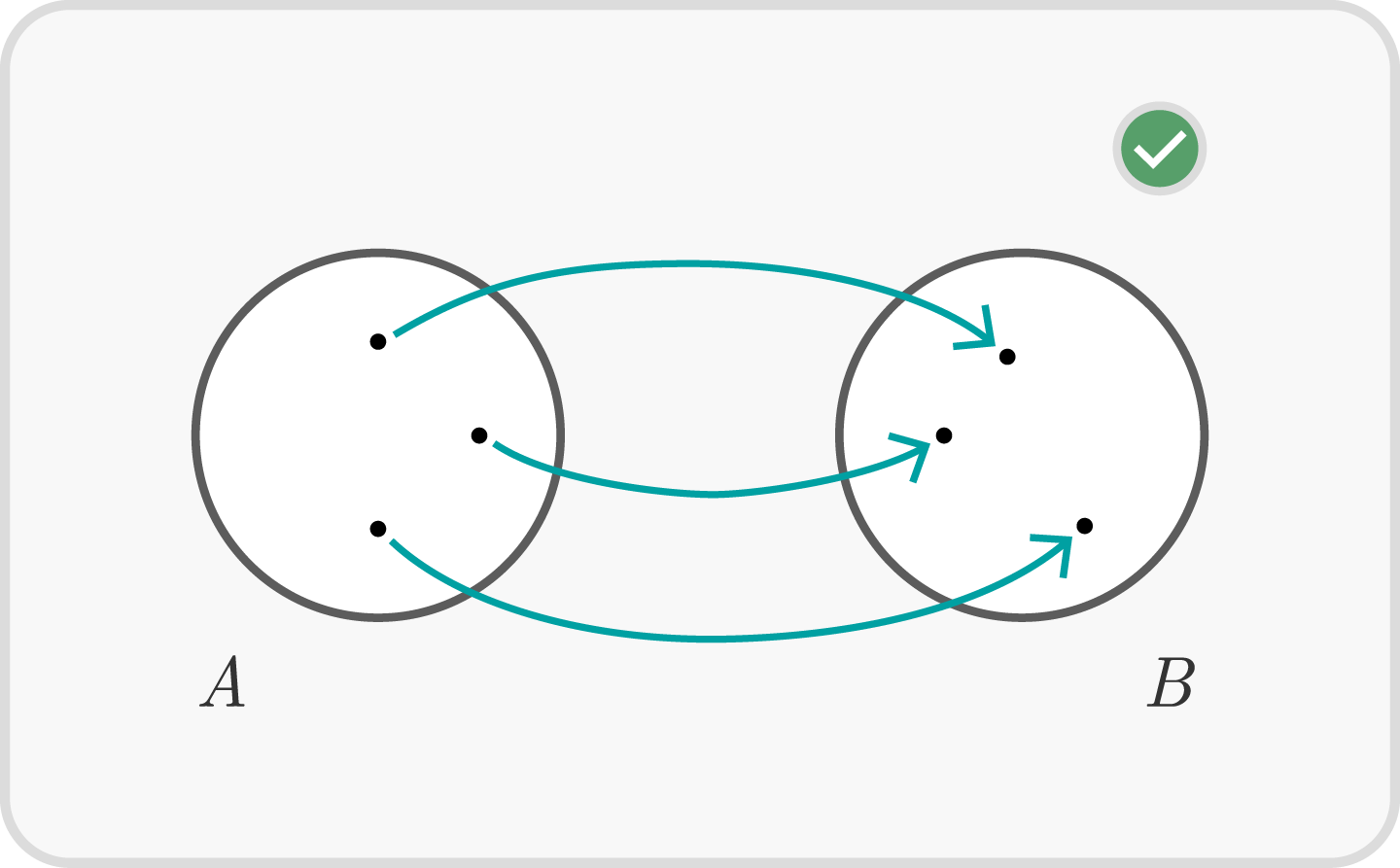
Definition 1.3
Sei $f: A \to B$ eine Abbildung.
- Ist $f(A) = B$, so heißt $f$ surjektiv (alle Werte aus $B$ werden getroffen).
- Gibt es für jedes $b \in B$ höchstens ein $a \in A$ mit $f(a)=b$, so heißt $f$ injektiv.
- Ist $f$ injektiv und surjektiv, so heißt $f$ bijektiv.
Bemerkung
-
Anders formuliert bedeutet Surjektivität, dass jeder Punkt aus $B$ mindestens einmal getroffen wird.
Injektivität bedeutet, dass jeder Punkt aus $B$ höchstens einmal getroffen wird.
Damit bedeutet Bijektivität, dass jeder Punkt aus $B$ genau einmal getroffen wird. -
Es gibt auch Abbildungen, die weder injektiv noch surjektiv sind.
Welche der Abbildungen sind surjektiv, aber nicht injektiv?
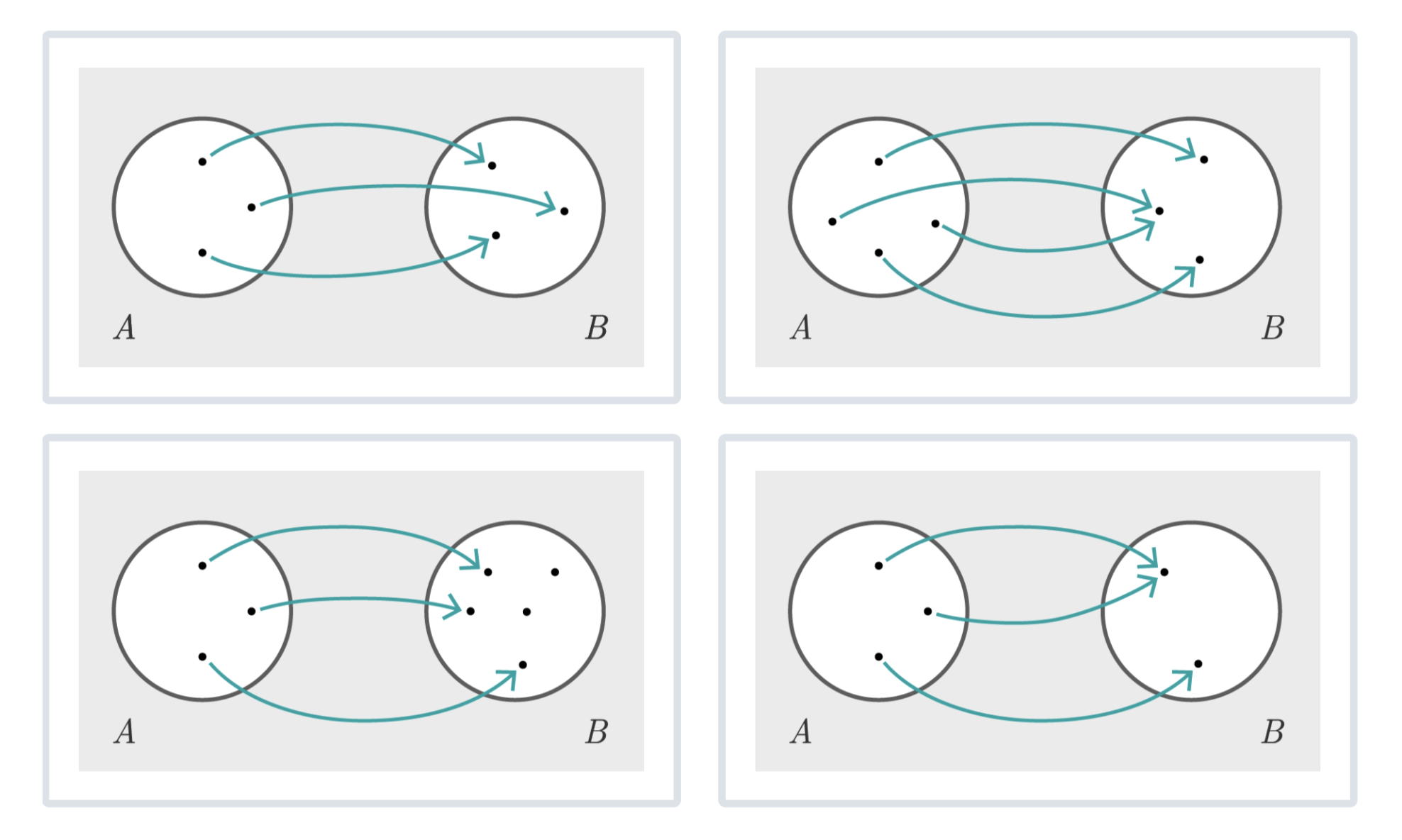
Lösung zum Aufklappen
Die Abbildungen rechts oben und rechts unten sind surjektiv, aber nicht injektiv.
Umkehrbare Abbildungen
Definition 1.4
Die Abbildung $f: A \to f(A) \subseteq B$ heißt umkehrbar, wenn für jedes $b \in B$ die Menge $f^{-1}(b)$ aus jeweils genau einem Element besteht.
Bemerkung
Die Formulierung $f^{-1}(b)$ mit $b \in B$ besteht aus jeweils genau einem Element bedeutet, dass zwei Eigenschaften gleichzeitig erfüllt sein müssen:
-
Das Urbild $f^{-1}(b)$ besteht für jedes $b \in B$ aus mindestens einem Element. Im vorherigen Abschnitt haben wir diese Eigenschaft Surjektivität genannt.
-
Das Urbild $f^{-1}(b)$ besteht für jedes $b \in B$ aus höchstens einem Element. Im vorherigen Abschnitt haben wir diese Eigenschaft Injektivität genannt.
Wir erhalten daraus den folgenden Satz:
Satz 1.1
Seien $A$ und $B$ Mengen. Jede bijektive Abbildung $f: A \to B$ ist umkehrbar und jede umkehrbare Abbildung ist bijektiv.
Beispiel
Seien
$A: = \{ x\;|\;x$ <em>nimmt an der Mathe I im aktuellen Semester teil</em>$\}$ und $B: = \{ y\;|\;y$ <em>ist ein Land auf der Welt</em>$\}$ Mengen.
Die Abbildung $f: A \to B$ ordnet jedem Studierenden bzw. jeder Studentin sein bzw. ihr Herkunftsland zu. $f(A)$ ist die Menge der vorkommenden Länder. Die Abbildung $f: A \to B$ ist nicht umkehrbar, da es Herkunftsländer gibt, die für mehrere Studierende zutreffen (keine Injektivität). Zudem gibt es sicherlich Länder, die nicht als Herkunftsländer der Studierenden von Mathe I vorkommen (keine Surjektivität).
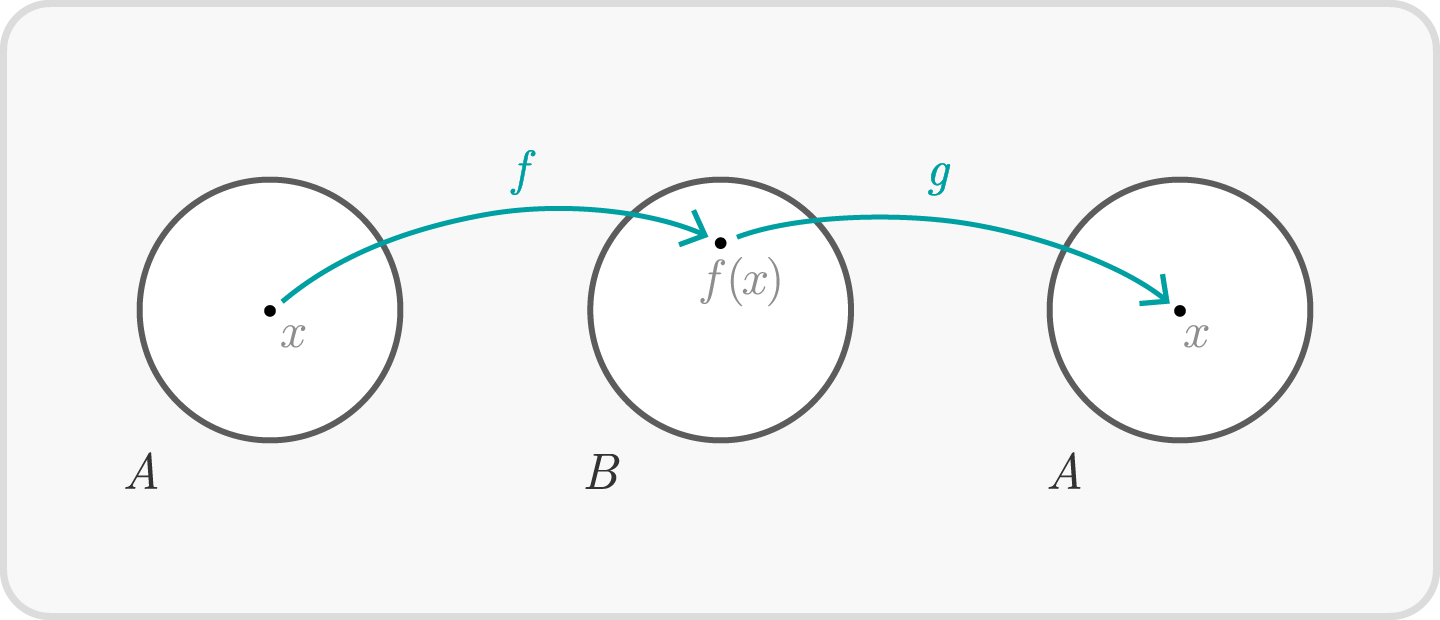
Satz 1.2
Die Abbildung $f: A \to B$ ist genau dann umkehrbar, wenn es eine Abbildung $g: B \to A$ gibt, für die gilt: $$g( f(x) ) = x \mbox{ f}\ddot{\rm u}\text{r alle } x \in A \qquad \mbox{und} \qquad f( g(y) ) = y \mbox{ f}\ddot{\rm u}\text{r alle } y \in B$$
Bemerkung
Die Formulierung „genau dann“ in dem Satz bedeutet, dass wir den Satz in beide Richtungen anwenden dürfen. Die eine Leserichtung lautet: Ist die Abbildung $f$ umkehrbar, dann gibt es eine Abbildung $g$ mit den genannten Eigenschaften. Die andere Leserichtung lautet: Gibt es zu der Abbildung $f$ eine Abbildung $g$ mit den genannten Eigenschaften, dann ist die Abbildung $f$ umkehrbar.
Welche der folgenden Abbildungen sind umkehrbar?
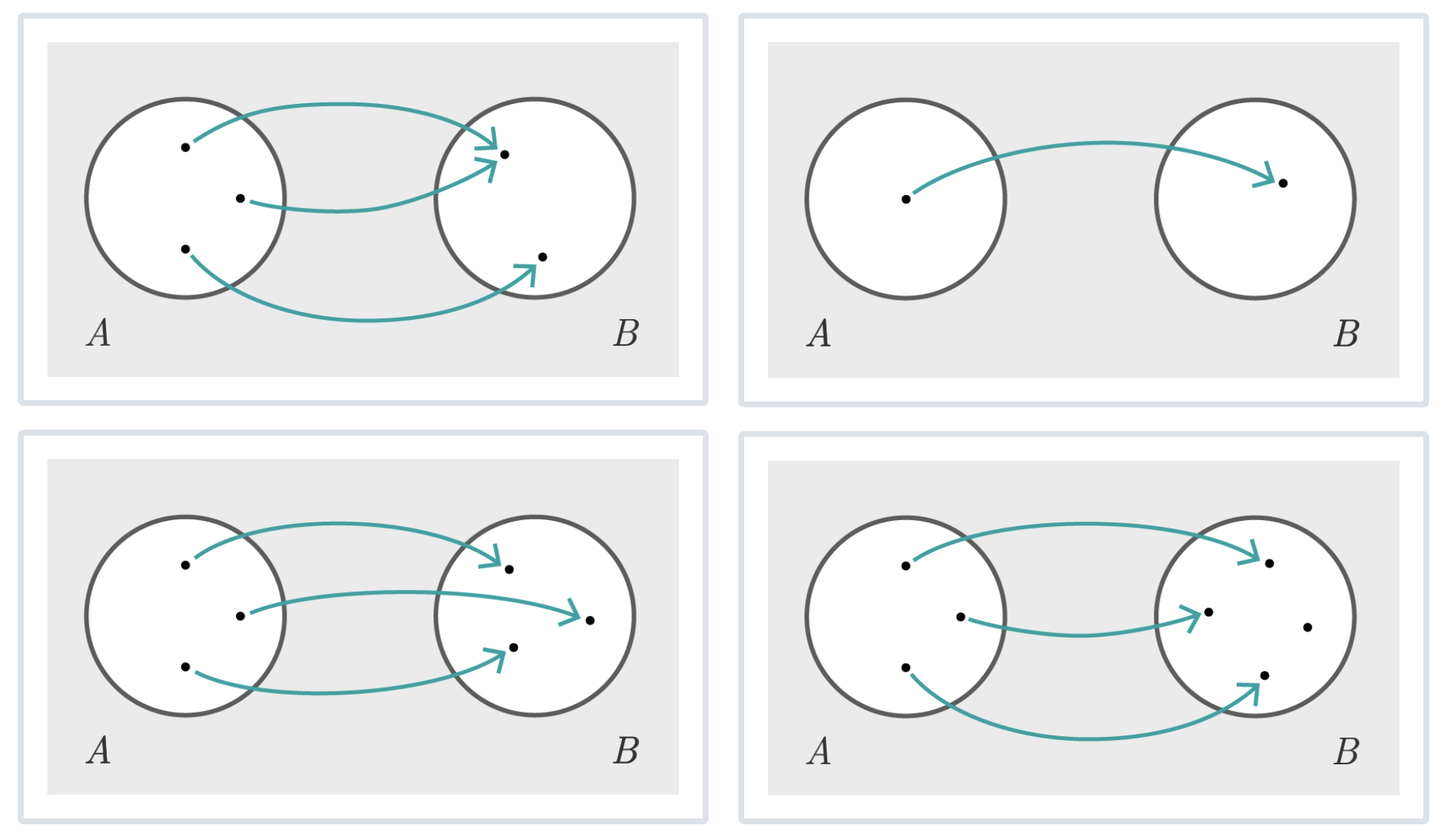
Lösung zum Aufklappen
Die Abbildung rechts oben und die Abbildung links unten sind umkehrbar.
Graphen von Abbildungen
Wir können Abbildungen zwischen Mengen, die aus endlich vielen Elementen
bestehen, über Kreise und Pfeile visualisieren. Wir würden aber gerne
auch Abbildungen zwischen Mengen mit unendlich vielen Elementen (z.B.
Intervallen in $\mathbb{R}$) visualisieren können.
Dazu brauchen wir das Kartesische Produkt von Mengen:
Definition 1.6: Kartesisches Produkt
Seien A, B Mengen und $n \in \mathbb{N}$. Dann ist $$ A \times B := \{ ( x,y ) \;| \;x \in A \mbox{ und } y \in B \} \quad \mbox{(wir sagen: '$A$ Kreuz $B$') } $$ das kartesische Produkt der Mengen $A$ und $B$. Es ist auch möglich, das kartesische Produkt einer Menge mit sich selbst zu bilden. Wir schreiben dann
$$ A^n := \{ ( x_1, \ldots ,x_n) \;|\; x_1, x_2, \ldots , x_n \in A \} .$$
Beispiel
Kartesische Produkte kennen Sie bereits aus Ihrem Alltag: Der uns umgebende Raum ist ein kartesisches Produkt.
$$\mathbb{R}^3 = \{ ( x_1, x_2, x_3 )\; |\; x_1,x_2,x_3 \in \mathbb{R} \}$$
Jeder Punkt im Raum kann durch drei Koordinaten identifiziert werden. Wir nennen die Koordinatenachsen auch $x$-Achse, $y$-Achse und $z$-Achse.
Wir schreiben oft die Elemente aus dem $\mathbb{R}^3$ als Spaltenvektoren, z.B. $$\left(\begin{array}{c} 1\\ 5\\ -3 \end{array} \right) \in \mathbb{R}^3$$
Beispiel
Beim zweidimensionalen Raum $\mathbb{R}^2$ betrachten wir Paare $(x,y)$ mit $x \in \mathbb{R}$ und $y \in \mathbb{R}$. Das Koordinatensystem ist dann ein Koordinatenkreuz. Die $x$-Achse zeigt nach rechts, die $y$-Achse nach oben.
Wir können in dem Koordinatenkreuz Mengen im $\mathbb{R}^2$ graphisch darstellen: $$M= \{ (x,y) \;|\; 0 \le x < 1 \text{ und } 1 < y \le 2 \}$$
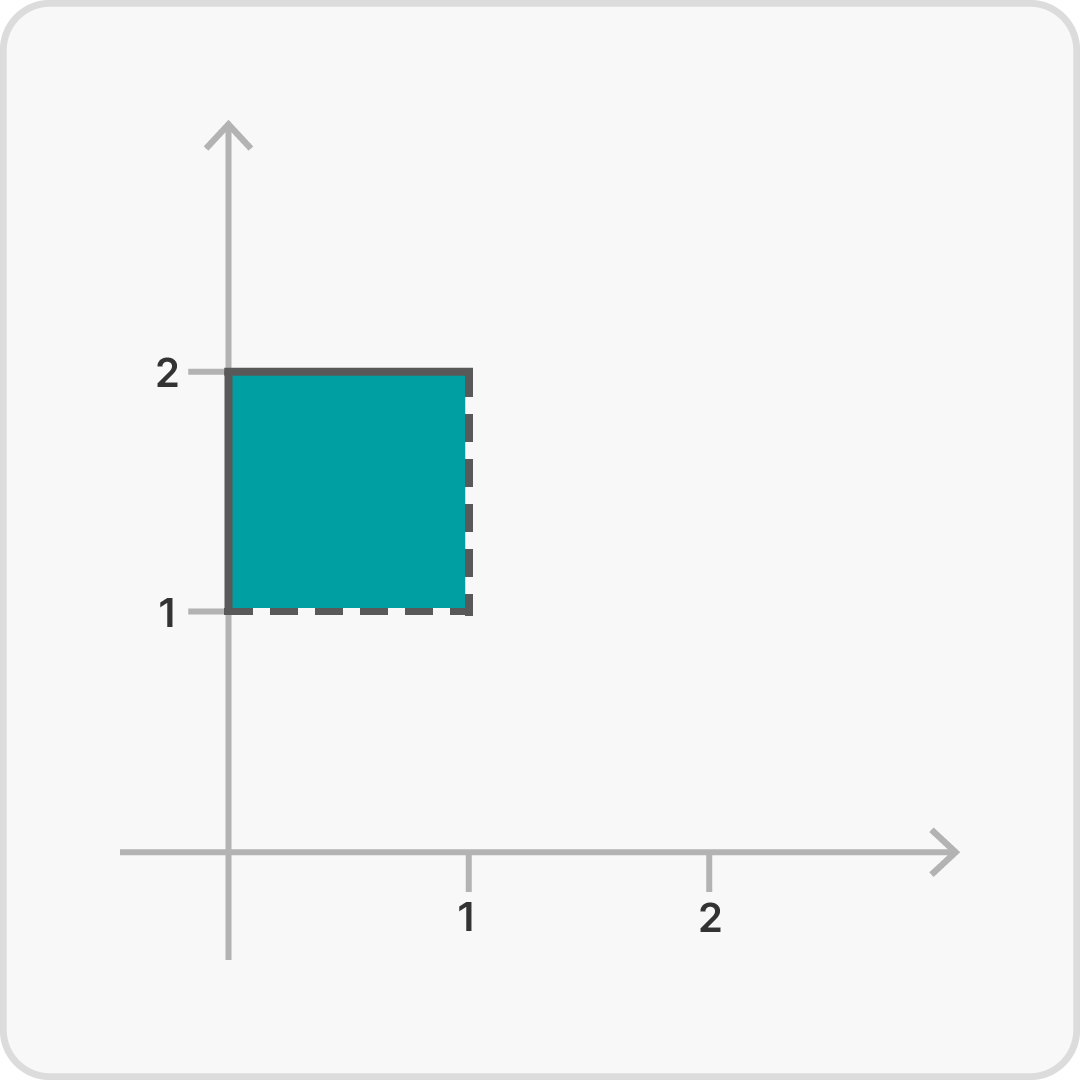
Wir werden die Darstellung zweier reeller Zahlen als Zahlenpaar im $\mathbb{R}^2$ verwenden, um Abbildungen graphisch darzustellen. Der Definitionsbereich gehört dabei stets zur $x$-Achse. Entweder nimmt er alle Werte der $x$-Achse ein oder nur einen Teil davon. Dem Wertebereich ordnen wir entsprechend die $y$-Achse zu. Jedes Paar $(x,f(x))$ beschreibt einen Punkt im $\mathbb{R}^2$, den wir als Punkt im Koordinatensystem mit $x$- und $y$-Achse darstellen können. Die Paare $(x,f(x))$ nennen wir auch Tupel. Alle Tupel stellen zusammen den Graphen der Abbildungen dar:
Definition 1.7
Sei $D \subseteq \mathbb{R}$ und $f: D \to \mathbb{R}$ eine Abbildung. Dann ist $$Graph(f) = \{ (x, f(x)) \in D \times \mathbb{R}\;|\; x \in D \}$$ der Graph von $f$.
Definition 1.8
Eine Abbildung, deren Wertebereich die reellen Zahlen $\mathbb{R}$ sind, nennen wir auch Funktion.
Beispiel
Wir wollen nun den Graphen der Funktion $$f: \mathbb{R} \to \mathbb{R} \quad \text{mit} \quad f(x) = x^2$$ zeichnen.
Definition 1.9
Eine Funktion $f: \mathbb{R} \to \mathbb{R}$ heißt
-
gerade, wenn $f(-x) = f(x)$ für jedes $x \in \mathbb{R}$.
-
ungerade, wenn $f(-x) = -f(x)$ für jedes $x \in \mathbb{R}$.
Wir können die Definitionen gerader und ungerader Funktionen verallgemeinern auf Funktionen $f: A \to \mathbb{R}$, wenn $A$ nur eine Teilmenge von $\mathbb{R}$ ist. Allerdings setzt dies voraus: Ist $x \in A$, dann gilt auch $–x \in A$.
Bemerkung
Der Graph einer geraden Funktion ist spiegelsymmetrisch zur $y$-Achse. Dies bedeutet, dass wenn wir einen Punkt des Graphen an der $y$-Achse spiegeln, wir dann wieder einen Punkt auf dem Graphen erhalten. Wir überprüfen dies durch die Gleichung $f(-x) = f(x)$.
Der Graph einer ungeraden Funktion ist punktsymmetrisch zum Ursprung. Dies bedeutet, dass wenn wir einen Punkt des Graphen am Ursprung spiegeln, wir dann wieder einen Punkt auf dem Graphen erhalten. Eine Punktspiegelung ist eine Drehung um 180°. Wir überprüfen dies durch die Gleichung $f(-x) = -f(x)$.
Lineare Funktionen
Definition 1.10
Seien $a,b \in \mathbb{R}$ und $a \not=0$. Eine Funktion $f: \mathbb{R} \to \mathbb{R}$ darstellbar durch $f(x)=ax+b$ heißt lineare Funktion.
In einer Wertetabelle bestimmen wir für mehrere Punkte aus dem Definitionsbereich die Tupel $(x,f(x))$. Wir übertragen sie in das Koordinatensystem und erhalten als Graphen der Funktion eine Gerade.
Diese Gerade schneidet für $x=0$ die $y$-Achse im Punkt $(0,b)$, denn $f(0)=a \cdot 0 + b=b$. Wir nennen $b$ den $y$-Achsenabschnitt.
Eine Gerade ist neben ihrer Funktionsvorschrift auch eindeutig durch die Vorgabe von zwei verschiedenen Punkten $(x_1, f(x_1))$ und $(x_2, f(x_2))$ festgelegt. Insbesondere ist $x_1 \not=x_2$.
Betrachten wir die Gleichungen der Funktion für diese Punkte, so erhalten wir $f(x_1)=a\cdot x_1 + b$ und $f(x_2)=a\cdot x_2 + b$. Subtrahieren wir diese voneinander, so erhalten wir $$f(x_1)-f(x_2)=a\cdot x_1 - a\cdot x_2.$$
Das $b$ ist in der neuen Gleichung nicht mehr enthalten, und wir können die Gleichung nach $a$ auflösen. $$\frac{f(x_1)-f(x_2)}{x_1 - x_2}=a.$$
Die Wahl der Punkte $(x_1, f(x_1))$ und $(x_2, f(x_2))$ war beliebig, doch der Wert dieses Quotienten $a$ ist unabhängig von der Wahl stets gleich. Wir nennen diese Konstante $a$ die Steigung der Geraden.
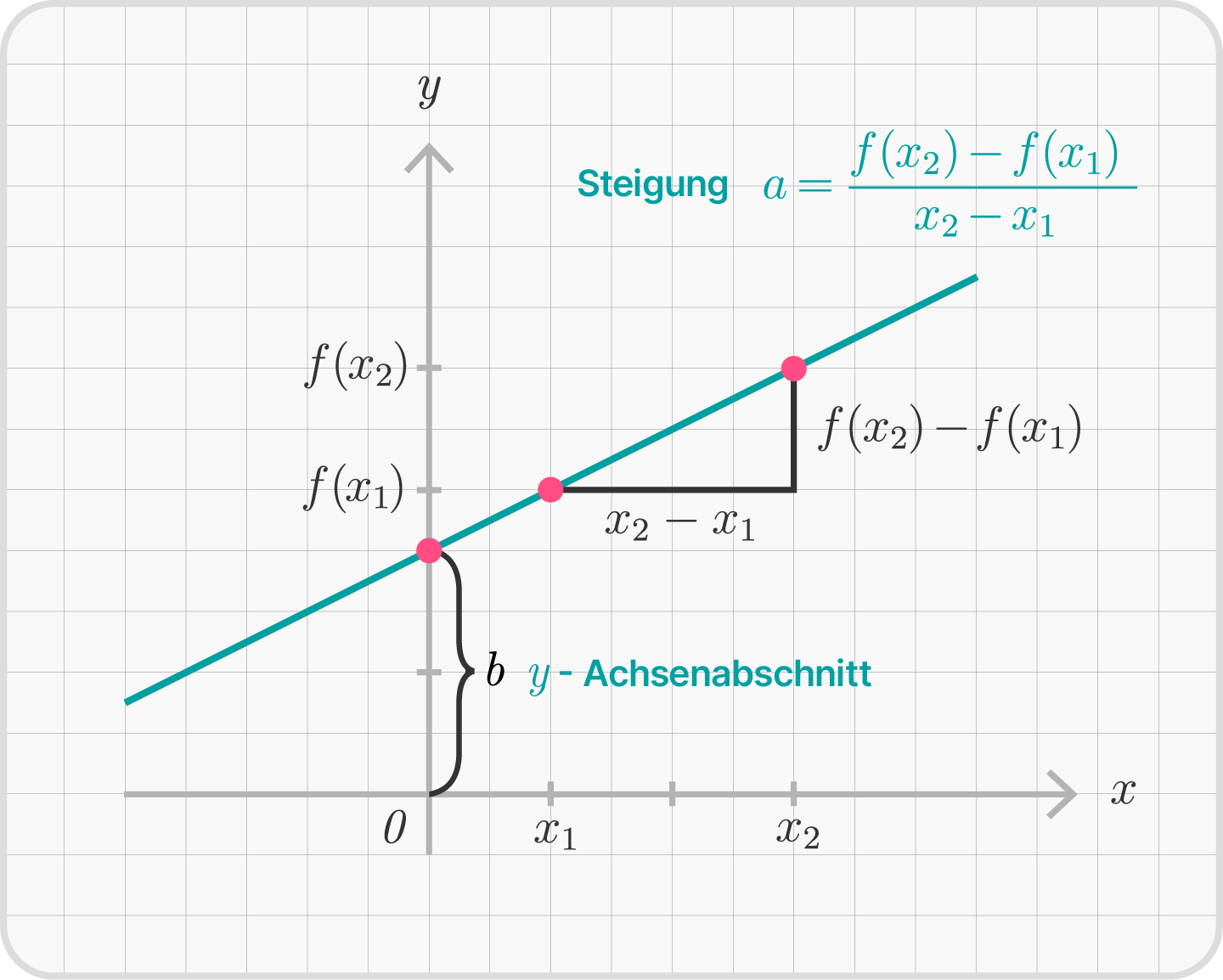
Probieren Sie nun selbst aus, wie sich der Graph der linearen Funktion $f(x)=ax+b$ verändert, wenn Sie die Werte für $a$ und $b$ variieren:
Die Lösungen von linearen Gleichungen der Form $ax+b=0$ haben hier eine geometrische Bedeutung. Es handelt sich um die Nullstellen der Funktion, d.h. es sind Punkte $x_0$, die eingesetzt in die Funktion $f(x)=ax+b$ null ergeben. (Anders formuliert: $x_0 \in \mathbb{R}$ mit $f(x_0)=0$)
Können Sie sich nicht mehr erinnern, wie lineare Gleichungen gelöst werden? Im Anhang finden Sie eine kurze Wiederholung dieses Themas.
Im Koordinatensystem sind Nullstellen Schnittpunkte mit der $x$-Achse, denn die
$x$-Achse enthält alle Paare $(x,0)$.
Ist $a \not=0$, so hat eine lineare Gleichung $ax+b=0$ genau eine Lösung $x_0=\frac{-b}{a}$.
Quadratische Funktionen
Definition 1.11
Seien $a,b,c \in \mathbb{R}$ und $a \not=0$. Eine Funktion $f: \mathbb{R} \to \mathbb{R}$ darstellbar durch $f(x)=ax^2 +bx + c$ heißt quadratische Funktion.
Wenn wir über eine Wertetabelle für mehrere Punkte aus dem
Definitionsbereich die Paare $(x,f(x))$ bestimmen und diese in das
Koordinatensystem übertragen, erhalten wir als Graphen eine sogenannte
Parabel. Die $y$-Achse enthält alle Werte $(0,y)$. Diese Parabel
schneidet daher die $y$-Achse im Punkt $(0,c)$, denn
$f(0)=a \cdot 0^2 + b \cdot 0 + c=c$. Wir nennen auch hier, wie bei
linearen Gleichungen, $c$ den $y$-Achsenabschnitt.
Ob eine Parabel nach oben oder nach unten geöffnet ist, wird durch den
Vorfaktor $a$ festgelegt: Ist $a>0$, dann ist die Parabel nach oben, ist
$a<0$, dann ist die Parabel nach unten geöffnet.
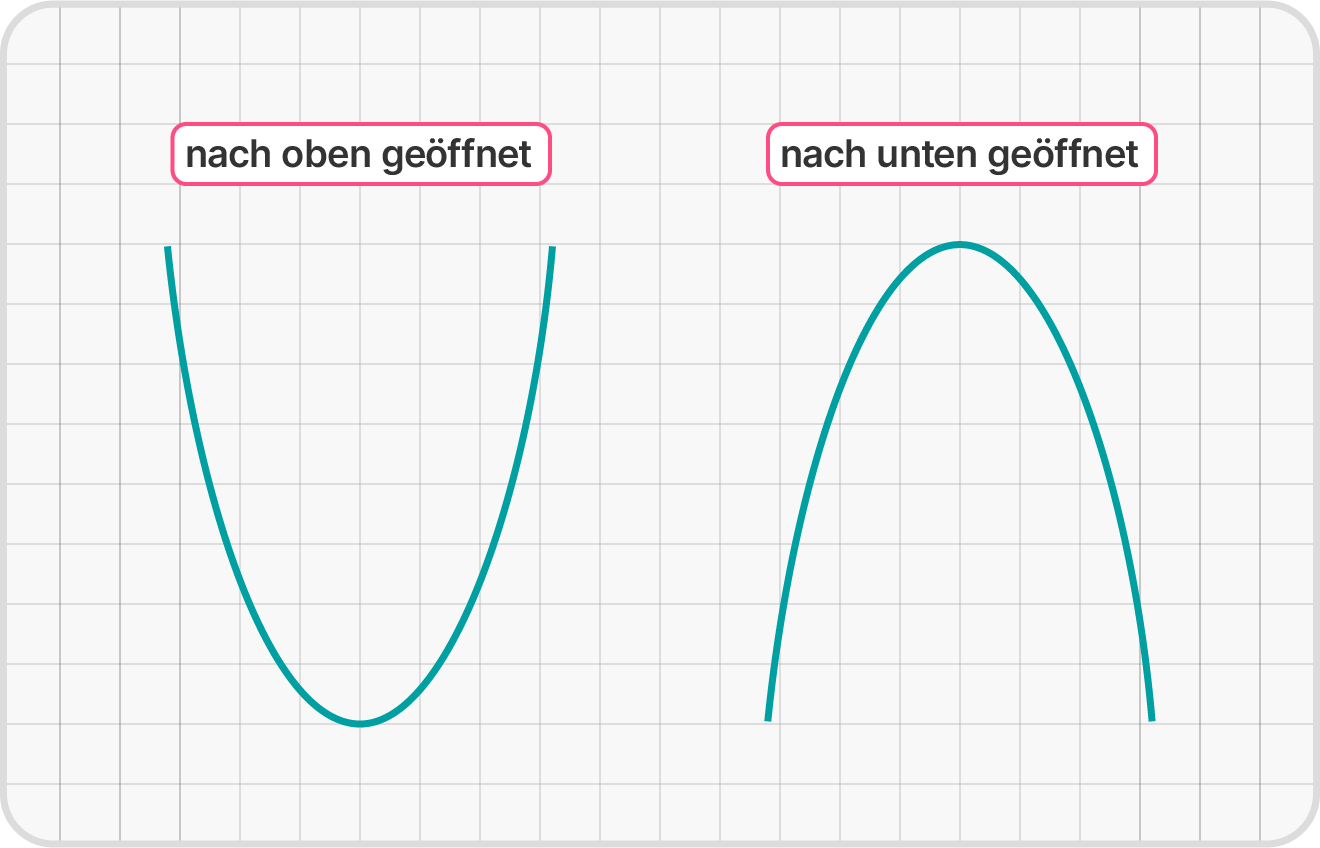
Um die Position einer Parabel im Koordinatensystem eindeutig festzulegen, berechnen wir den Scheitelpunkt der Parabel. Dieser ist der kleinste bzw. der größte Funktionswert der quadratischen Funktion.
Wir wollen uns zuerst ansehen, wie wir den Scheitelpunkt einer Parabel
für einfache Fälle von quadratischen Funktionen bestimmen können:
Fall 1) $f(x)=x^2$. Der Graph ist die sogenannte Normalparabel (Es gilt: $a=1$, $b=0$ und $c=0$). Wir haben sie bereits früher in dieser Lerneinheit visualisiert, siehe Graphen von Funktionen. Wenn wir reelle Zahlen quadrieren, dann ist das Ergebnis stets größer oder gleich null. Quadrieren wir eine von null verschiedene Zahl, so ist das Ergebnis größer null. Der kleinste Wert dieser quadratischen Funktion wird daher in $x=0$ erreicht. Der Scheitelpunkt hat damit die Koordinaten $S=(0,f(0))=(0,0)$.
Fall 2) $f(x)=ax^2$. Diese Funktion unterscheidet sich vom Fall 1) durch den Vorfaktor $a$, den Streckungsfaktor. Dieser Vorfaktor vergrößert, verkleinert oder ändert das Vorzeichen aller unserer Funktionswerte und verändert so die Form unserer Parabel. Er ändert aber nichts an der Position und den Koordinaten des Scheitelpunktes.
Achtung!
Durch den Streckungsfaktor bleibt der Scheitelpunkt erhalten, aber die Parabel wird gestreckt oder bestaucht.
Beim Zeichnen gehen wir wie folgt vor:
Wir tragen den Scheitelpunkt ins Koordinatensystem ein. Dann gehen wir von diesem jeweils einen $1$-Schritt in $x$-Richtung nach rechts und links. Und dann gehen wir in $y$-Richtung jeweils einen Schritt mit dem Wert $a$. Dieser Schritt geht nach oben oder unten, in Abhängigkeit von dem Vorzeichen von $a$. Durch diese beiden neuen Koordinatenpunkte und den Scheitelpunkt verläuft die Parabel.
Fall 3) $f(x)=x^2+d$. Der Summand $d$ ändert die Position der Parabel entlang der $y$-Achse Durch Veränderung von $d$ verschiebt sich die Parabel nach oben oder unten. Der $x$-Wert des Scheitelpunkts bleibt konstant. Der Funktionswert verändert sich in Abhängigkeit von $d$. Die Koordinaten des Scheitelpunkts sind damit $S=(0,f(0))=(0,d).$
Fall 4) $f(x)=(x+s)^2$. Hier betrachten wir eine andere Darstellung einer quadratischen Funktion. Der Summand $s$ im quadratischen Term ändert
die Position der Parabel entlang der $x$-Achse. Durch Veränderung von
$s$ verschiebt sich die Parabel nach links oder rechts um $s$, wobei ein
positives $s$ eine Verschiebung nach links und ein negatives $s$ eine
Verschiebung nach rechts bewirkt. Der Funktionswert des Scheitelpunkts
bleibt dabei konstant. Die Koordinaten des Scheitelpunkts sind damit
$S=(-s,0)$.
Nun wollen wir den allgemeinen Fall einer quadratischen Funktion betrachten. Ihren Scheitelpunkt können wir mithilfe der quadratischen Ergänzung berechnen.
Erinnern Sie sich noch, wie das Verfahren quadratische Ergänzung funktioniert? Falls nicht, so finden Sie eine kurze Wiederholung dieses Themas im Anhang.
Wir können eine quadratische Funktion $f(x)$ wie folgt umformen: $$f(x)=ax^2+bx+c = a(x+\frac{b}{2a})^2 - \frac{b^2}{4a} + c$$ Mit den Erkenntnissen aus der Fallunterscheidung 1-4 folgern wir, dass der Scheitelpunkt bei $S=(-s,d)=(-\frac{b}{2a}, - \frac{b^2}{4a} + c)$ liegt. Die Darstellung $f(x)=(x+s)^2+d$ nennen wir auch die Scheitelpunktform.
Anhang
Auf den nun folgenden Seiten finden Sie den Anhang. Dieser wiederholt das Lösen von lineare und quadratischen Gleichungen. Falls Ihnen die eine oder andere Rechentechnik nicht mehr geläufig ist, können Sie dies hier auf den nächsten Seiten wiederholen.
Anhang: Äquivalenzumformungen
Wir werden in diesem Abschnitt verschiedene Arten von Gleichungen betrachten und ihre Lösungen berechnen.
Um eine Lösung einer linearen Gleichung zu bestimmen, müssen wir die Gleichung umformen. Unsere Umformung darf die Lösung aber nicht verändern. Wir werden in dieser Lerneinheit sehen, dass eine Gleichung eine oder mehrere Lösungen haben kann. Auch die Zahl der Lösungen darf sich durch unsere Umformungen nicht verändern.
Umformungen, die diese beiden Eigenschaften haben, nennen wir Äquivalenzumformungen.
Wenn sich Lösungen von Gleichungen durch Umformungen verändern, handelt es sich demnach um keine Äquivalenzumformungen. Hier sehen wir dazu drei Beispiele:
Beispiel 1: Quadrieren einer Gleichung
Wir betrachten die Gleichung $x-2=4$. Durch Ausprobieren sehen wir, dass für $x=6$ die Gleichung erfüllt wird. $x=6$ ist damit eine Lösung. Wenn wir die Gleichung quadrieren, erhalten wir $(x-2)^2=16$. Für diese Gleichung sind sowohl $x=6$ als auch $x=-2$ Lösungen. Die ursprüngliche Gleichung wird durch $x=-2$ aber nicht gelöst. Also haben wir durch das Quadrieren die Zahl der Lösungen der Gleichung erhöht. Quadrieren ist keine Äquivalenzumformung.
Beispiel 2: Ziehen einer positiven Wurzel
Wir betrachten die Gleichung $(x+2)^2=9$. Durch Ausprobieren sehen wir, dass die Gleichung sowohl durch $x=1$ als auch $x=-5$ gelöst wird. Wenn wir aus der Gleichung die positive Wurzel ziehen, erhalten wir $x+2=3$. Diese Gleichung wird weiterhin durch $x=1$ gelöst, aber nicht mehr durch $x=-5$. Also haben wir durch das Ziehen der positiven Wurzel die Zahl der Lösungen der Gleichung verkleinert. Ziehen der positiven Wurzel ist keine Äquivalenzumformung.
Beispiel 3: Multiplikation mit null
Wir betrachten die Gleichung $x-1=5$ Diese Gleichung wird durch $x=6$ gelöst, aber z.B. durch $x=2$ nicht. Wenn wir die Gleichung mit null multiplizieren, erhalten wir $0\cdot(x-1)=0\cdot 5$. Diese Gleichung $0=0$ hängt nicht von $x$ ab, daher sind alle reellen Zahlen als Lösungen erlaubt. Aber die Lösungen $x=0$ oder $x=3$ sind keine Lösungen der ursprünglichen Gleichung. Also haben wir durch die Multiplikation mit null die Zahl der Lösungen erhöht. Dies ist keine Äquivalenzumformung.
Anhang: Lösungen linearer Gleichungen
Wir beginnen mit der einfachsten Gleichungsart, den linearen Gleichungen:
Definition A.1
Unter einer reellen linearen Gleichung für die Variable $x \in \mathbb{R}$ verstehen wir eine Gleichung der Form:
Bei linearen Gleichungen sind als Äquivalenzumformungen die folgenden Operationen erlaubt: Die Addition und Subtraktion von Zahlen und Termen sowie die Multiplikation und Division von Zahlen und Termen, die von null verschieden sind.
Hinweis
Beim Umformen von Gleichungen geben wir am rechten Rand der Gleichung hinter einem Strich oder in Klammern jeweils an, welche Umformung wir durchgeführt haben. Dies macht es einfacher, die Äquivalenzumformungen nachzuvollziehen. Bei Äquivalenzumformungen setzen wir das Zeichen $\Leftrightarrow$ zwischen die äquivalenten Gleichungen.
Die Lösung einer linearen Gleichung können wir so bestimmen:
$$ \begin{array}{rcl} ax+b &= & 0 \quad \big| -b\\\\ \Leftrightarrow \quad ax &=& -b \quad \big| :a \quad (\text{dies ist m}\ddot{\rm o}\text{glich, da }a \not=0)\\\\ \Leftrightarrow \quad x&=& -\frac{b}{a} \end{array} $$Für zwei konkrete Zahlenwerte $a=2$ und $b=-6$ lautet die Gleichung: $2x-6=0$. Die Lösung dieser Gleichung ist: $x=- \frac{-6}{2}=3$.
Die nächste Aufgabe verwendet das Eingabeformat Äquivalenz-Checker. Sie finden eine Erklärung dazu im Tutorial über digitale Aufgaben. Falls Sie es noch nicht kennen, schauen Sie es sich dort zuerst an, bevor Sie die Aufgabe bearbeiten.
Anhang: Lösungen quadratischer Gleichungen
Nun führen wir einen weiteren Typ von Gleichungen ein, die quadratischen Gleichungen:
Definition A.2
Unter einer reellen quadratischen Gleichung für die Variable $x \in \mathbb{R}$ verstehen wir eine Gleichung der Form:
Eine quadratische Gleichung kann eine, zwei oder keine Lösung haben.
Wir nennen $D=\frac{b^2}{4a^2} - \frac{c}{a}$ die Diskriminante. Die Diskriminante gibt uns Auskunft darüber, wie viele Lösungen wir erhalten:
- Ist $D>0, \quad$ dann existiert die reelle Wurzel $\sqrt{D}$ und die quadratische Gleichung hat genau zwei Lösungen $x_1= -\frac{b}{2a} + \sqrt{D}$ und $x_2=-\frac{b}{2a} - \sqrt{D}$.
- Ist $D=0, \quad$ dann existiert die reelle Wurzel $\sqrt{D}=0$ und die quadratische Gleichung hat genau eine Lösung $x=-\frac{b}{2a}$.
- Ist $D<0, \quad$ dann existiert die reelle Wurzel $\sqrt{D}$ nicht und wir erhalten keine Lösung.
Wir wollen jetzt herleiten, warum die Lösungen der quadratischen Gleichung genau diese Form haben. Dazu nutzen wir die binomischen Formeln $(x+y)^2=x^2+2xy+y^2$ und $(x-y)^2=x^2-2xy+y^2$. Die notwendige Umformung heißt quadratische Ergänzung.
Für einen übersichtlichen Rechenweg betrachten wir nur den Spezialfall $a=1$. Wir werden bei der Umformung eine Wurzel aus beiden Seiten der Gleichung ziehen müssen. Wir wissen bereits, dass das Ziehen der positiven Wurzel keine Äquivalenzumformung ist. Wenn wir beim Wurzelziehen sowohl die positive als auch negative Wurzel betrachten, verändern wir die Lösungen nicht. Dies ist dann eine Äquivalenzumformung. Wir bezeichnen diese Umformung mit $\pm \sqrt{\;\;}$.
\begin{array} {rcl} 0& = & x^2 + bx + c \qquad \big| \ \text{(in Form der ersten binom. Formel bringen)} \\\\ \Leftrightarrow \qquad 0 & = & (\underbrace{x^2}_{= x^2} + 2 \cdot \underbrace{x}_{=x} \cdot \underbrace{\frac{b}{2}}_{= y}+ \underbrace{\left(\frac{b}{2}\right)^2}_{= y^2} - \left(\frac{b}{2}\right)^2) + c \qquad \big| \ \text{(Umformung in bin. Formel)}\\\\ \Leftrightarrow \qquad 0& = & (x+\frac{b}{2})^2 - \frac{b^2}{4} + c \qquad \big| + \frac{b^2}{4}-c \\\\ \Leftrightarrow \qquad \frac{b^2}{4} - c & = & (x+\frac{b}{2})^2\qquad \big| \pm \sqrt{\;\;}\\\\ \Leftrightarrow \qquad \pm \sqrt{\frac{b^2}{4} - c }& = & x+\frac{b}{2} \\\\ \Leftrightarrow \qquad -\frac{b}{2} \pm \sqrt{\frac{b^2}{4} -c }& = & x \end{array}Die Bestimmung der Lösung fassen wir für den Fall $a=1$, $b=p$ und $c=q$ mit $p,q \in \mathbb{R}$ über die sogenannte „p-q-Formel” zusammen:
Satz A.1: p-q-Formel
Die Lösungen der reellen quadratischen Gleichung $x^2+px+q=0$ mit $p,q \in \mathbb{R}$ lauten: $$x_1= -\frac{p}{2} + \sqrt{\left(\frac{p}{2}\right)^2 - q} \qquad \text{ und } \qquad x_2=-\frac{p}{2} - \sqrt{\left(\frac{p}{2}\right)^2 - q}.$$ $x_1$ und $x_2$ können verschieden sein, gleich sein oder nicht existieren.
Die nächste Aufgabe verwendet das Eingabeformat Äquivalenz-Checker. Sie finden eine Erklärung dazu im Tutorial über digitale Aufgaben. Falls Sie es noch nicht kennen, schauen Sie es sich dort zuerst an, bevor Sie die Aufgabe bearbeiten.