1 - Pre Learning (Buch)

Lineare Funktionen

In einer Wertetabelle bestimmen wir für mehrere Punkte aus dem Definitionsbereich die Tupel $(x,f(x))$. Wir übertragen sie in das Koordinatensystem und erhalten als Graphen der Funktion eine Gerade.

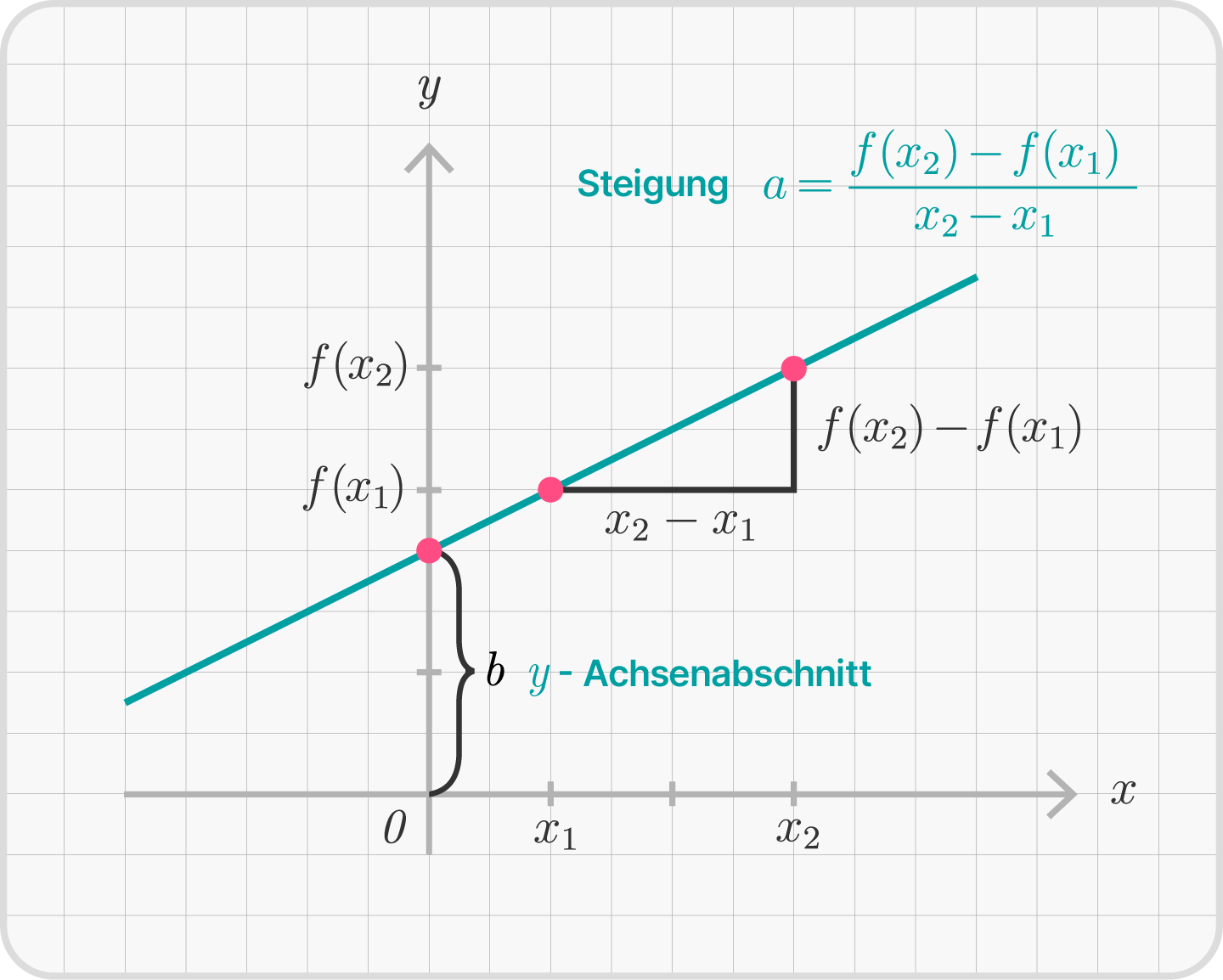
Diese Gerade schneidet für $x=0$ die $y$-Achse im Punkt $(0,b)$, denn $f(0)=a \cdot 0 + b=b$. Wir nennen $b$ den $y$-Achsenabschnitt.

Eine Gerade ist neben ihrer Funktionsvorschrift auch eindeutig durch die Vorgabe von zwei verschiedenen Punkten $(x_1, f(x_1))$ und $(x_2, f(x_2))$ festgelegt. Insbesondere ist $x_1 \not=x_2$.

Betrachten wir die Gleichungen der Funktion für diese Punkte, so erhalten wir $f(x_1)=a\cdot x_1 + b$ und $f(x_2)=a\cdot x_2 + b$. Subtrahieren wir diese voneinander, so erhalten wir $$f(x_1)-f(x_2)=a\cdot x_1 - a\cdot x_2.$$

Das $b$ ist in der neuen Gleichung nicht mehr enthalten, und wir können die Gleichung nach $a$ auflösen. $$\frac{f(x_1)-f(x_2)}{x_1 - x_2}=a.$$

Die Wahl der Punkte $(x_1, f(x_1))$ und $(x_2, f(x_2))$ war beliebig, doch der Wert dieses Quotienten $a$ ist unabhängig von der Wahl stets gleich. Wir nennen diese Konstante $a$ die Steigung der Geraden.

Probieren Sie nun selbst aus, wie sich der Graph der linearen Funktion $f(x)=ax+b$ verändert, wenn Sie die Werte für $a$ und $b$ variieren:

Die Lösungen von linearen Gleichungen der Form $ax+b=0$ haben hier eine geometrische Bedeutung. Es handelt sich um die Nullstellen der Funktion, d.h. es sind Punkte $x_0$, die eingesetzt in die Funktion $f(x)=ax+b$ null ergeben. (Anders formuliert: $x_0 \in \mathbb{R}$ mit $f(x_0)=0$)

Können Sie sich nicht mehr erinnern, wie lineare Gleichungen gelöst werden? Im Anhang finden Sie eine kurze Wiederholung dieses Themas.

Im Koordinatensystem sind Nullstellen Schnittpunkte mit der $x$-Achse, denn die $x$-Achse enthält alle Paare $(x,0)$.
Ist $a \not=0$, so hat eine lineare Gleichung $ax+b=0$ genau eine Lösung $x_0=\frac{-b}{a}$.