1 - Pre Learning (Buch)
Graphen von Abbildungen
Wir können Abbildungen zwischen Mengen, die aus endlich vielen Elementen
bestehen, über Kreise und Pfeile visualisieren. Wir würden aber gerne
auch Abbildungen zwischen Mengen mit unendlich vielen Elementen (z.B.
Intervallen in $\mathbb{R}$) visualisieren können.
Dazu brauchen wir das Kartesische Produkt von Mengen:
Definition 1.6: Kartesisches Produkt
Seien A, B Mengen und $n \in \mathbb{N}$. Dann ist $$ A \times B := \{ ( x,y ) \;| \;x \in A \mbox{ und } y \in B \} \quad \mbox{(wir sagen: '$A$ Kreuz $B$') } $$ das kartesische Produkt der Mengen $A$ und $B$. Es ist auch möglich, das kartesische Produkt einer Menge mit sich selbst zu bilden. Wir schreiben dann
$$ A^n := \{ ( x_1, \ldots ,x_n) \;|\; x_1, x_2, \ldots , x_n \in A \} .$$
Beispiel
Kartesische Produkte kennen Sie bereits aus Ihrem Alltag: Der uns umgebende Raum ist ein kartesisches Produkt.
$$\mathbb{R}^3 = \{ ( x_1, x_2, x_3 )\; |\; x_1,x_2,x_3 \in \mathbb{R} \}$$
Jeder Punkt im Raum kann durch drei Koordinaten identifiziert werden. Wir nennen die Koordinatenachsen auch $x$-Achse, $y$-Achse und $z$-Achse.
Wir schreiben oft die Elemente aus dem $\mathbb{R}^3$ als Spaltenvektoren, z.B. $$\left(\begin{array}{c} 1\\ 5\\ -3 \end{array} \right) \in \mathbb{R}^3$$
Beispiel
Beim zweidimensionalen Raum $\mathbb{R}^2$ betrachten wir Paare $(x,y)$ mit $x \in \mathbb{R}$ und $y \in \mathbb{R}$. Das Koordinatensystem ist dann ein Koordinatenkreuz. Die $x$-Achse zeigt nach rechts, die $y$-Achse nach oben.
Wir können in dem Koordinatenkreuz Mengen im $\mathbb{R}^2$ graphisch darstellen: $$M= \{ (x,y) \;|\; 0 \le x < 1 \text{ und } 1 < y \le 2 \}$$
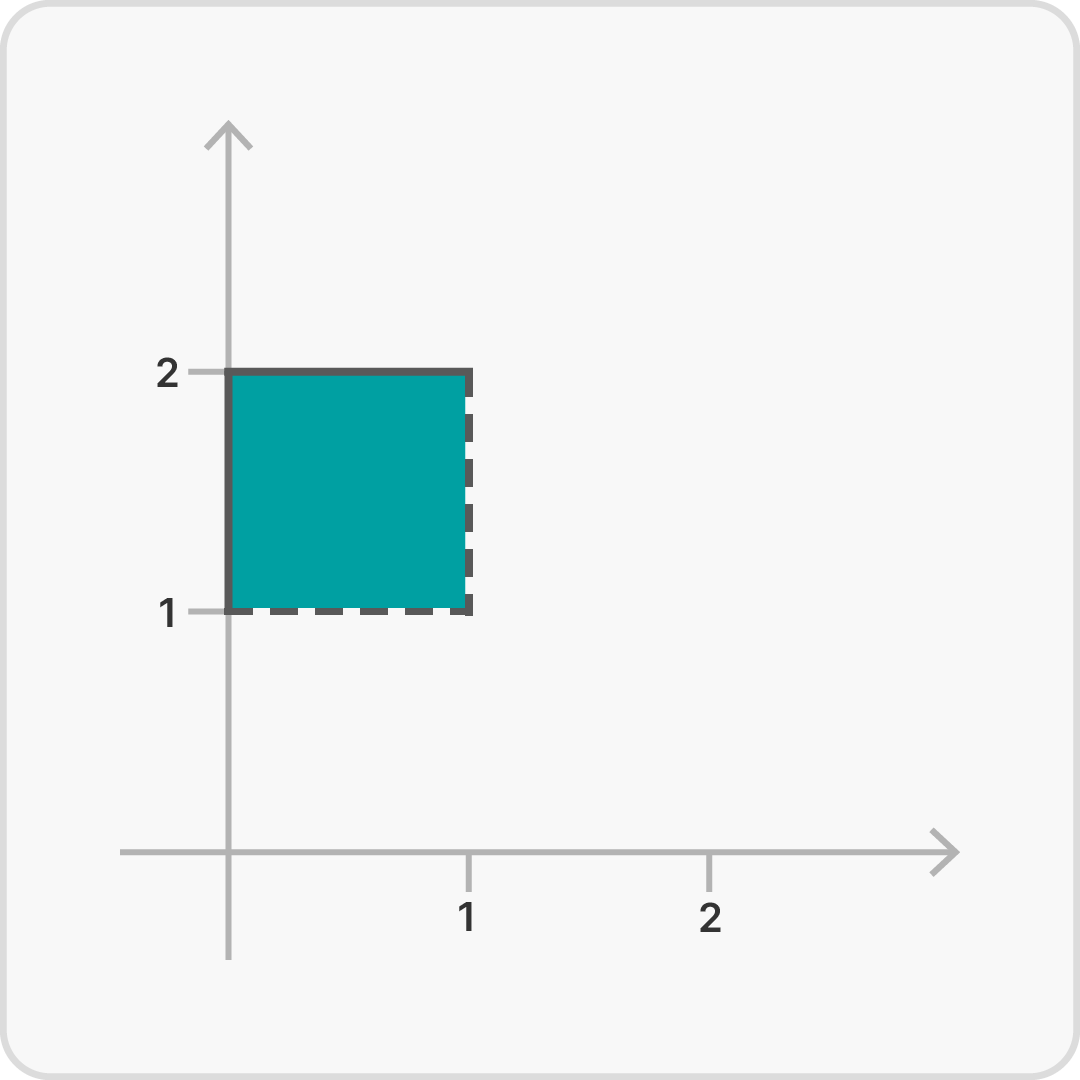
Wir werden die Darstellung zweier reeller Zahlen als Zahlenpaar im $\mathbb{R}^2$ verwenden, um Abbildungen graphisch darzustellen. Der Definitionsbereich gehört dabei stets zur $x$-Achse. Entweder nimmt er alle Werte der $x$-Achse ein oder nur einen Teil davon. Dem Wertebereich ordnen wir entsprechend die $y$-Achse zu. Jedes Paar $(x,f(x))$ beschreibt einen Punkt im $\mathbb{R}^2$, den wir als Punkt im Koordinatensystem mit $x$- und $y$-Achse darstellen können. Die Paare $(x,f(x))$ nennen wir auch Tupel. Alle Tupel stellen zusammen den Graphen der Abbildungen dar:
Definition 1.7
Sei $D \subseteq \mathbb{R}$ und $f: D \to \mathbb{R}$ eine Abbildung. Dann ist $$Graph(f) = \{ (x, f(x)) \in D \times \mathbb{R}\;|\; x \in D \}$$ der Graph von $f$.
Definition 1.8
Eine Abbildung, deren Wertebereich die reellen Zahlen $\mathbb{R}$ sind, nennen wir auch Funktion.
Beispiel
Wir wollen nun den Graphen der Funktion $$f: \mathbb{R} \to \mathbb{R} \quad \text{mit} \quad f(x) = x^2$$ zeichnen.
Definition 1.9
Eine Funktion $f: \mathbb{R} \to \mathbb{R}$ heißt
-
gerade, wenn $f(-x) = f(x)$ für jedes $x \in \mathbb{R}$.
-
ungerade, wenn $f(-x) = -f(x)$ für jedes $x \in \mathbb{R}$.
Wir können die Definitionen gerader und ungerader Funktionen verallgemeinern auf Funktionen $f: A \to \mathbb{R}$, wenn $A$ nur eine Teilmenge von $\mathbb{R}$ ist. Allerdings setzt dies voraus: Ist $x \in A$, dann gilt auch $–x \in A$.
Bemerkung
Der Graph einer geraden Funktion ist spiegelsymmetrisch zur $y$-Achse. Dies bedeutet, dass wenn wir einen Punkt des Graphen an der $y$-Achse spiegeln, wir dann wieder einen Punkt auf dem Graphen erhalten. Wir überprüfen dies durch die Gleichung $f(-x) = f(x)$.
Der Graph einer ungeraden Funktion ist punktsymmetrisch zum Ursprung. Dies bedeutet, dass wenn wir einen Punkt des Graphen am Ursprung spiegeln, wir dann wieder einen Punkt auf dem Graphen erhalten. Eine Punktspiegelung ist eine Drehung um 180°. Wir überprüfen dies durch die Gleichung $f(-x) = -f(x)$.
