1 - Pre Learning (Buch)
Umkehrbare Abbildungen
Definition 1.4
Die Abbildung $f: A \to f(A) \subseteq B$ heißt umkehrbar, wenn für jedes $b \in B$ die Menge $f^{-1}(b)$ aus jeweils genau einem Element besteht.
Bemerkung
Die Formulierung $f^{-1}(b)$ mit $b \in B$ besteht aus jeweils genau einem Element bedeutet, dass zwei Eigenschaften gleichzeitig erfüllt sein müssen:
-
Das Urbild $f^{-1}(b)$ besteht für jedes $b \in B$ aus mindestens einem Element. Im vorherigen Abschnitt haben wir diese Eigenschaft Surjektivität genannt.
-
Das Urbild $f^{-1}(b)$ besteht für jedes $b \in B$ aus höchstens einem Element. Im vorherigen Abschnitt haben wir diese Eigenschaft Injektivität genannt.
Wir erhalten daraus den folgenden Satz:
Satz 1.1
Seien $A$ und $B$ Mengen. Jede bijektive Abbildung $f: A \to B$ ist umkehrbar und jede umkehrbare Abbildung ist bijektiv.
Beispiel
Seien
$A: = \{ x\;|\;x$ <em>nimmt an der Mathe I im aktuellen Semester teil</em>$\}$ und $B: = \{ y\;|\;y$ <em>ist ein Land auf der Welt</em>$\}$ Mengen.
Die Abbildung $f: A \to B$ ordnet jedem Studierenden bzw. jeder Studentin sein bzw. ihr Herkunftsland zu. $f(A)$ ist die Menge der vorkommenden Länder. Die Abbildung $f: A \to B$ ist nicht umkehrbar, da es Herkunftsländer gibt, die für mehrere Studierende zutreffen (keine Injektivität). Zudem gibt es sicherlich Länder, die nicht als Herkunftsländer der Studierenden von Mathe I vorkommen (keine Surjektivität).
Satz 1.2
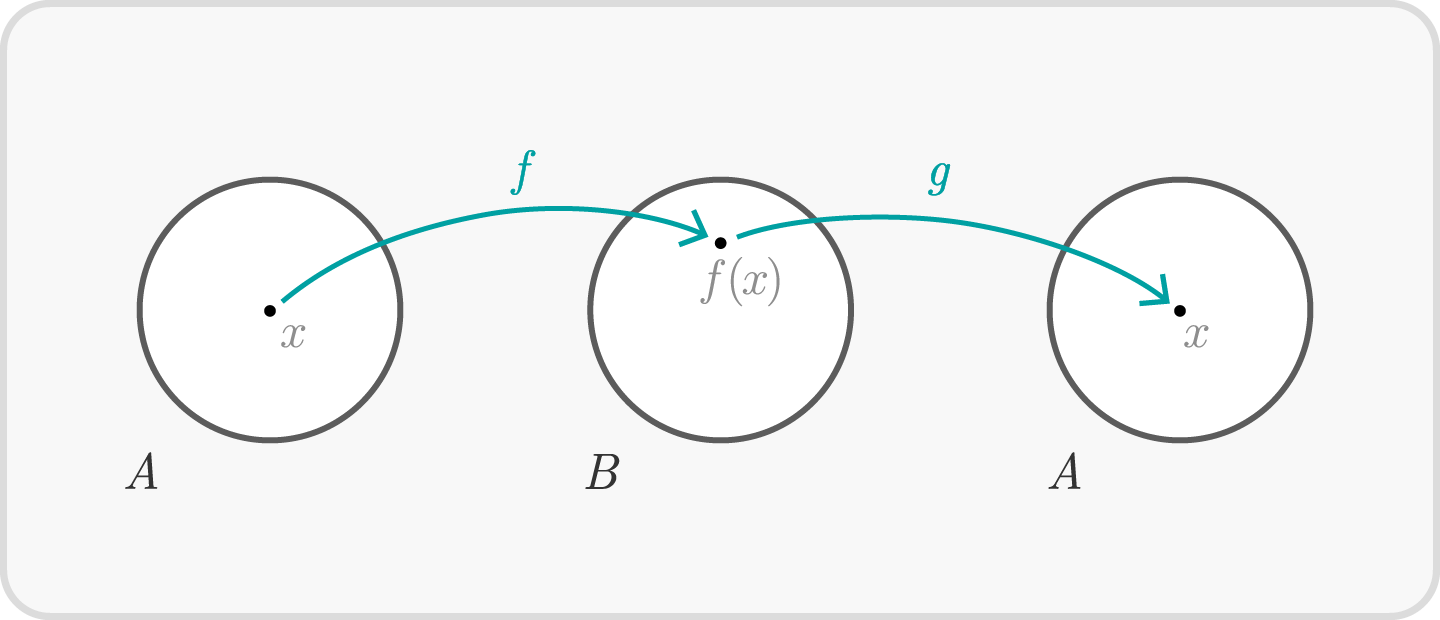
Die Abbildung $f: A \to B$ ist genau dann umkehrbar, wenn es eine Abbildung $g: B \to A$ gibt, für die gilt: $$g( f(x) ) = x \mbox{ f}\ddot{\rm u}\text{r alle } x \in A \qquad \mbox{und} \qquad f( g(y) ) = y \mbox{ f}\ddot{\rm u}\text{r alle } y \in B$$
Bemerkung
Die Formulierung „genau dann“ in dem Satz bedeutet, dass wir den Satz in beide Richtungen anwenden dürfen. Die eine Leserichtung lautet: Ist die Abbildung $f$ umkehrbar, dann gibt es eine Abbildung $g$ mit den genannten Eigenschaften. Die andere Leserichtung lautet: Gibt es zu der Abbildung $f$ eine Abbildung $g$ mit den genannten Eigenschaften, dann ist die Abbildung $f$ umkehrbar.
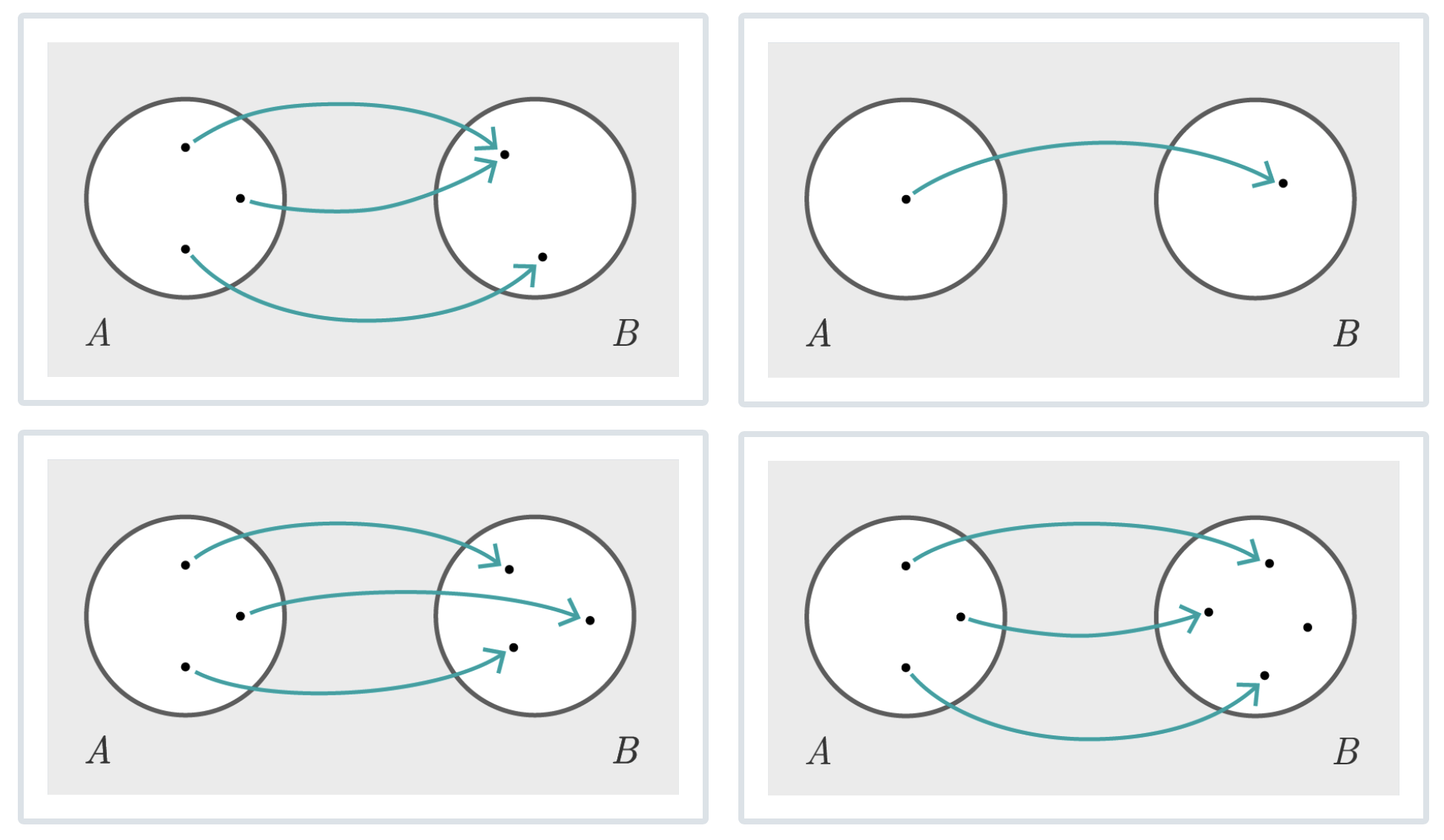
Welche der folgenden Abbildungen sind umkehrbar?
Lösung zum Aufklappen
Die Abbildung rechts oben und die Abbildung links unten sind umkehrbar.
