1 - Pre Learning (Buch)
Injektive, surjektive und bijektive Abbildungen
Wir kennen bereits die Eigenschaften, die eine Zuordnung haben muss, damit sie eine Abbildung zwischen zwei Mengen ist. In diesem Abschnitt werden wir zwei Eigenschaften von Abbildungen kennenlernen, über die wir spezielle Abbildungen charakterisieren können.
Definition 1.3
Sei $f: A \to B$ eine Abbildung.
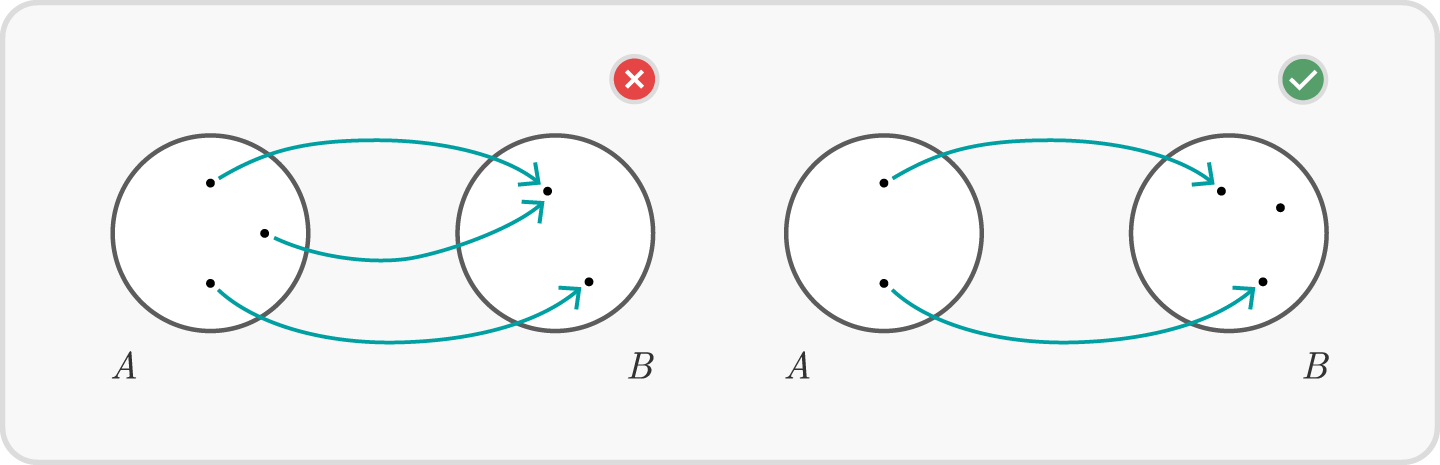
- Ist $f(A) = B$, so heißt $f$ surjektiv (alle Werte aus $B$ werden getroffen).
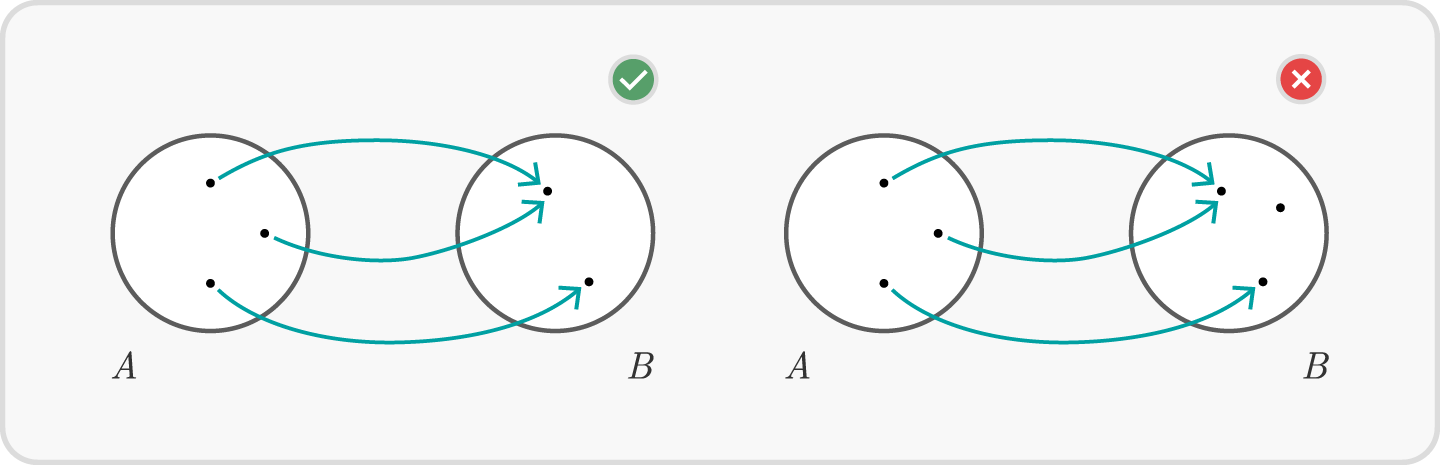
- Gibt es für jedes $b \in B$ höchstens ein $a \in A$ mit $f(a)=b$, so heißt $f$ injektiv.
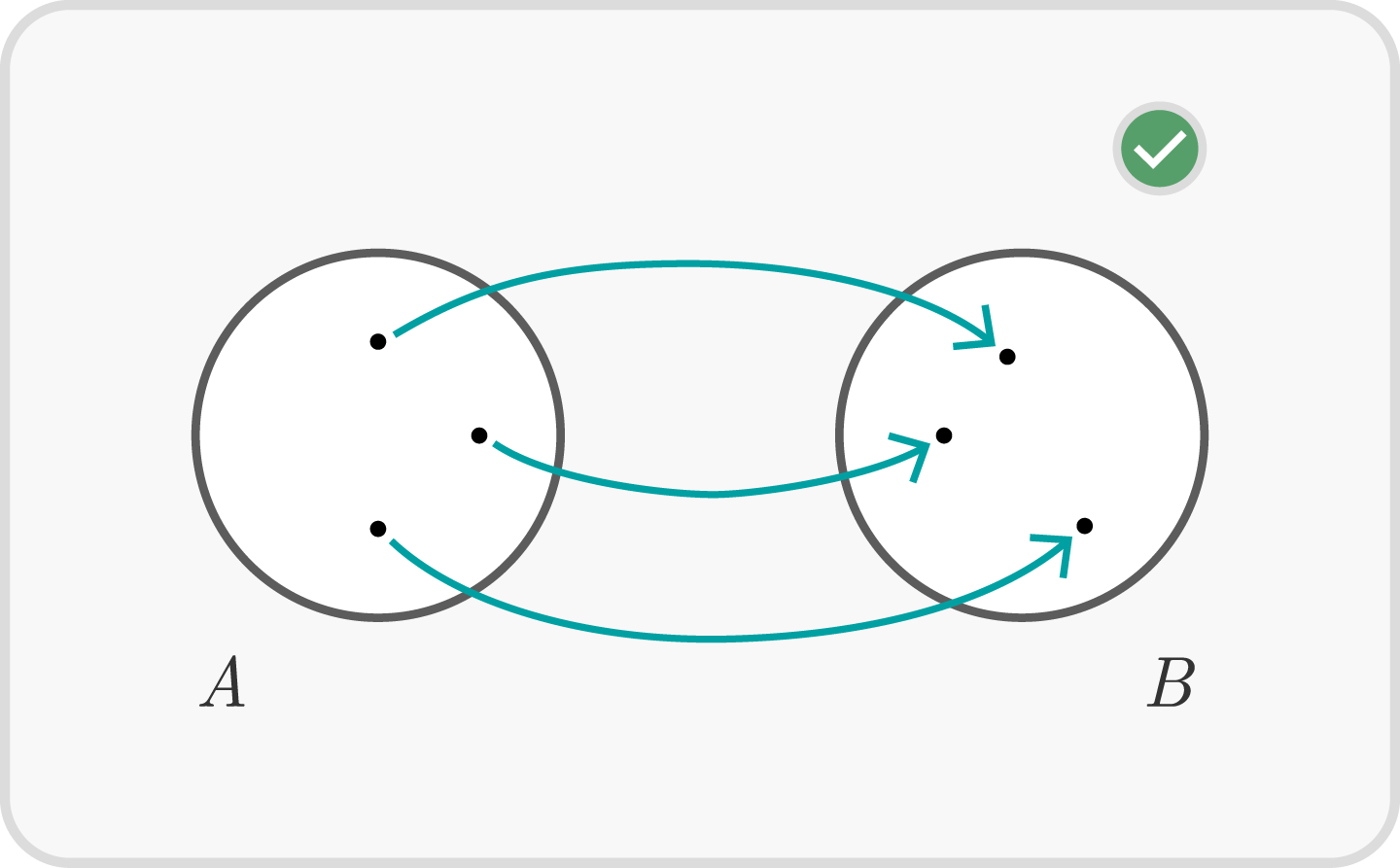
- Ist $f$ injektiv und surjektiv, so heißt $f$ bijektiv.
Bemerkung
-
Anders formuliert bedeutet Surjektivität, dass jeder Punkt aus $B$ mindestens einmal getroffen wird.
Injektivität bedeutet, dass jeder Punkt aus $B$ höchstens einmal getroffen wird.
Damit bedeutet Bijektivität, dass jeder Punkt aus $B$ genau einmal getroffen wird. -
Es gibt auch Abbildungen, die weder injektiv noch surjektiv sind.
Welche der Abbildungen sind surjektiv, aber nicht injektiv?
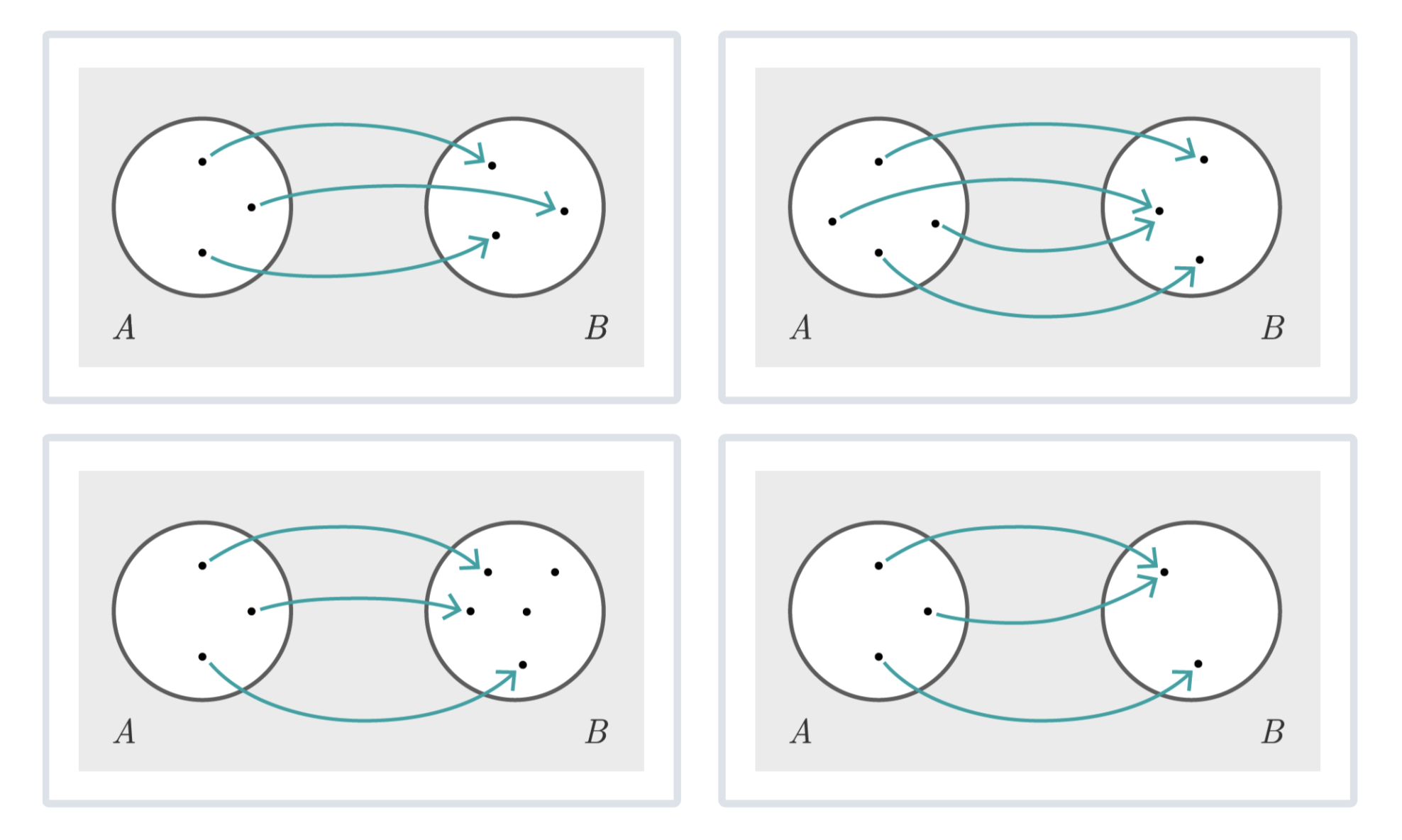
Lösung zum Aufklappen
Die Abbildungen rechts oben und rechts unten sind surjektiv, aber nicht injektiv.
