1 - Pre Learning (Buch)
Urbilder von Mengen
Definition 1.2
Sei $f : A \to B$ eine Abbildung und $b \in B$. Dann
ist das Urbild $$f^{-1}(b) = \{ a \in A \;|\; f(a) = b \}$$ von $b$
die Menge aller Elemente von $A$, die auf $b$ abgebildet werden.
Sei nun $C \subseteq B$. Dann heißt
$$f^{-1}(C) = \{ a \in A \;|\; f(a) \in C \}$$ das Urbild von
$C$. Es ist die Vereinigung aller $f^{-1}(c)$ mit $c \in C$.
Es gilt $f^{-1}(B) = A$, denn jedes Element von $A$ besitzt ein Bild in $B$.
Bemerkung
Wir sagen: $f^{-1}(C)$ ist das Urbild von $C$ unter $f$.
Beispiel
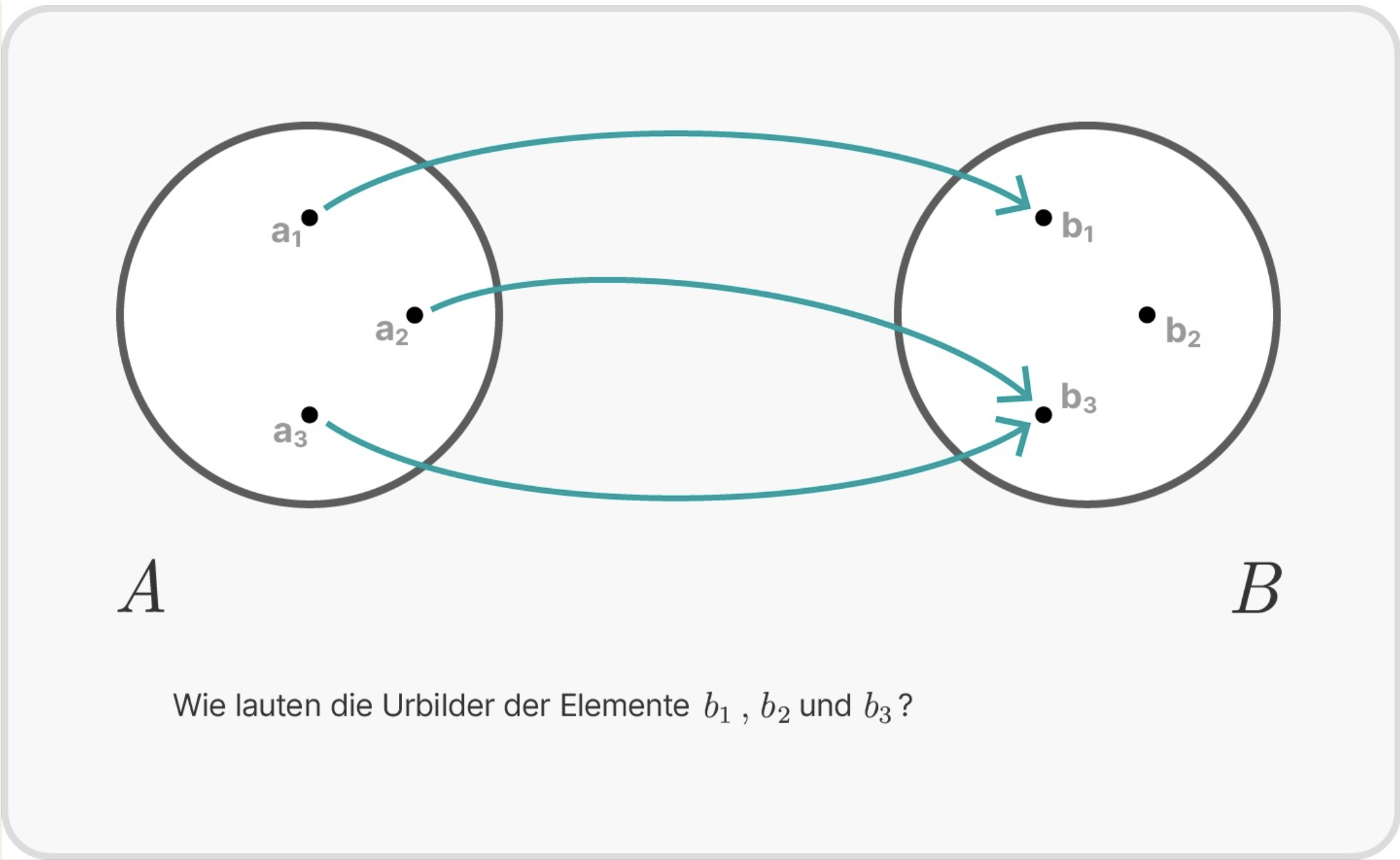
Lösung zum Aufklappen
Das Urbild von $b_1$ ist eine einelementige Menge und enthält nur das Element $a_1$. Wir schreiben_ $f^{-1}(b_1)=\{a_1\}$.
Das Urbild von $b_2$ ist leer. Wir schreiben_ $f^{-1}(b_2)=\{\}$.
Das Urbild von $b_3$ ist eine zweielementige Menge. Sie enthält die Elemente $a_2$ und $a_3$. Wir schreiben_ $f^{-1}(b_3)=\{a_2, a_3\}$.
