14.1a Das bestimmte Integral (Fortsetzung)
14.1 Das bestimmte Integral(Fortsetzung)
Nachdem das Integral nun definiert ist, wollen wir noch nachprüfen, dass die Eigenschaften, die uns am Anfang wünschenswert erschienen, nun auch tatsächlich erfüllt sind.
-
\(\alpha f+ \beta g\) ist Riemann-integrierbar mit
\(\displaystyle \int_a^b\alpha f+\beta g\,\mathrm{d}x=\alpha\int_a^b f\,\mathrm{d}x+\beta\int_a^b g\,\mathrm{d}x\)
-
Falls \(f(x)\leq g(x)\) für alle \(x\in [a,b]\), dann ist \(\displaystyle\int\limits_ a^b f( x) \, \mathrm{d}x\leq \int\limits_a^b g( x) \, \mathrm{d}x\)
Beweis:
-
folgt aus den Überlegungen zu Riemann-Summen, denn für eine Partition \(P\) mit \(a=x_0< x_1<\dots< x_n=b\) und Stützstellen \(\xi _ j\in [x_{j-1},x_ j]\) ist
\(Z_P(\alpha f+\beta g)=\sum\limits_{j=1}^n(x_j-x_{j-1})\alpha f(\xi_j)+\beta g(\xi_j)=\alpha Z_P(f)+\beta Z_P(g)\)
-
folgt ebenfalls aus Betrachtungen zu Riemann-Summen durch Grenzübergang, denn es ist
\(Z_P(f)=\sum\limits_{j=1}^n(x_j-x_{j-1})f(\xi_j)\leq\sum\limits_{j=1}^n(x_j-x_{j-1})g(\xi_j)=Z_P(g)\)
für jede Partition und jede Wahl von Stützstellen.
?
Insbesondere folgt aus 2., dass für \(f\geq 0\) auch \(\int\limits_ a^b f( x) \, \mathrm{d}x \geq 0\) ist.
-
die Riemann-integrierbaren Funktionen auf dem Intervall \([a,b]\) einen (unendlich-dimensionalen) Vektorraum bilden und
-
man das Riemann-Integral auch als eine lineare Abbildung von diesem Vektorraum aller integrierbaren Funktionen in die reellen Zahlen auffassen kann.
Den Übergang von einer Summe zum Integral kann man sich auch anhand eines Beispiels aus der Mechanik veranschaulichen.
Der Teil des Balkens zwischen \(x_ j\) und \(x_{j+1}\) übt nach der Formel
Drehmoment= Kraft \(\times \( Hebelarm das Drehmoment
\(N_j=\underbrace{g\varrho q(x_j)(x_{j+1}-x_j)}_{\text{Gewichtskraft}F_j}\cdot x_j\)
aus, wobei \(g\) die Erdbeschleunigung, \(\varrho (x)\) die Dichte und \(q(x_ j)\) die Querschnittsfläche des Balkens bei \(x=x_ j\) ist.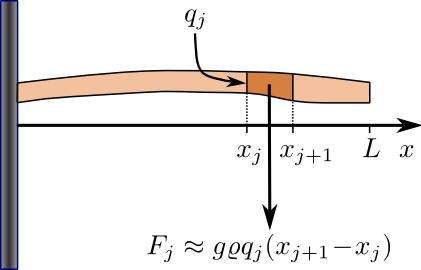
Das gesamte Drehmoment erhält man durch Summation über alle Teile als
\(N=\sum\limits_{j=1}^ng\varrho(x)q(x_j)(x_{j+1}-x_j)\cdot x_j\)
und durch immer feinere Unterteilung geht diese Summe in ein Integral über:\(N=\int\limits_0^Lg\varrho(x)q(x)\cdot x\,\mathrm{d}x.\)
Speziell für konstanten Querschnitt \(q(x)\equiv q\) und konstante Dichte \(\varrho (x)\equiv \varrho \):\(\displaystyle N=\int\limits_0^L g\varrho q\cdot x\,\mathrm{d}x=\frac{1}{2}g\varrho q L^2=\frac{1}{2}mgL\)
wobei \(m=\varrho q L\) die Masse des Balkens ist.An dieser Stelle soll noch überprüft werden, dass auch die dritte Eigenschaft, die wir gerne bei Integralen erfüllt haben wollten, tatsächlich gilt:
Sei \(f\colon [a,b]\to \mathbb {R}\) Riemann-integrierbar und \(c\in (a,b)\) gegeben. Dann gilt:
\(\displaystyle\int\limits_a^bf(x)\,\mathrm{d}x=\int\limits_a^cf(x)\,\mathrm{d}x+\int\limits_c^bf(x)\,\mathrm{d}x\)
Beweis: Jede Partition von \([a,b]\) können wir durch Hinzufügen des Punktes \(c\) zu einer Partition \(P\) machen, die sich in eine Partition \(P’\) von \([a,c]\) und eine Partition \(P”\) von \([c,b]\) unterteilen, der Feinheiten jeweils kleiner oder gleich der Feinheit von \(P\) sind und für die
\(Z_P( f)=Z_{P'}(f)+Z_{P''}( f)\)
gilt. Wenn also die Feinheit \(\delta _ P\to 0\) konvergiert, dann streben auch \(\delta _{P'}\to 0\) und \(\delta _{P''}\to 0\). Die linke Seite konvergiert dann gegen \(\int _ a^ bf( x)\, \mathrm{d}x\), während die rechte Seite gegen \(\int _ a^ c f(x)\, \mathrm{d}x+\int _ c^ bf( x)\, \mathrm{d}x\) konvergiert.
?
-
\(|f|\) ist Riemann-integrierbar und
\(\displaystyle\left|\int_a^b f(x)\,\mathrm{d}x\right|\leq\int_a^b|f|\,\mathrm{d}x\)
-
Sind \(f\) und \(g\) Riemann-integrierbar, dann sind auch die Funktionen \(\min \{ f,g\} ,\max \{ f,g\} :\; [a,b]\to \mathbb {R}\) Riemann-integrierbar und es gilt
\(\displaystyle\int\limits_a^b\min\{f,g\}\,\mathrm{d}x\leq\min\{\int_a^b f( x)\,\mathrm{d}x,\int_a^b g(x)\,\mathrm{d}x\}\)
sowie
\(\displaystyle\int\limits_a^b\max\{f,g\}\,\mathrm{d}x\geq\max\{\int\limits_a^b f\,\mathrm{d}x,\int\limits_a^b g\,\mathrm{d}x\}.\)
Beweis:
- Für jedes feste \(x\in [a,b]\) ist
\(-|f( x)|\leq f( x)\leq |f( x)|\)
Damit folgt dann aus der Positivität des Integrals
\(\displaystyle -\int\limits_a^b|f(x)|\,\mathrm{d}x\leq\int\limits_a^b f\,\mathrm{d}x\leq\int\limits_a^b|f(x)|\,\mathrm{d}x.\)
-
Es gilt
\(\min\{f,g\}=\displaystyle\frac{f+g-|f-g|}{2}\) und \(\max\{f,g\}=\displaystyle\frac{f+g+|f-g|}{2}\)
Daher folgt die Behauptung aus Teil 1 und der Linearität des Integrals.
?
Sei \(f\colon [a,b]\to \mathbb{R}\) durch \(f( x)=x\) gegeben. Dann gilt:
\(\displaystyle \int\limits_a^b f( x)\,\mathrm{d}x=\displaystyle\frac{b^2-a^2}{2}\)
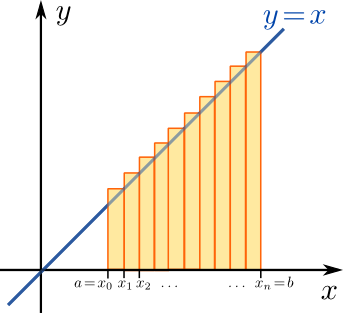
Sei \(P_ n\) die äquidistante Partition \(a=x_0<x_1<\dots< x_n=b\) mit \(x_j=a+j\cdot n = \displaystyle\frac{b-a}{n}\). Die Feinheit \(\delta_{P_n}=\displaystyle\frac{b-a}{n}\) wird für \(n\to\infty\) immer kleiner und es gilt:
\(\displaystyle\begin{array}{rcl}Z_{P_n}(f)&=&\sum\limits_{j=1}^n\underbrace{\displaystyle\frac{b-a}{n}}_{=x_{j+1}-x_j}f\underbrace{\left(a+j\displaystyle\frac{b-a}{n}\right)}_{=\xi_j}=\sum\limits_{j=1}^n\displaystyle\frac{b-a}{n}\left(a+j\displaystyle\frac{b-a}{n}\right)\\&&\\&=&\sum\limits_{j=1}^n\left(a+j\displaystyle\frac{b-a}{n}\right)\displaystyle\frac{b-a}{n}\;\;=\;\;\displaystyle\frac{b-a}{n}\left(na+\displaystyle\frac{b-a}{n}\sum\limits_{j=1}^nj\right)\\&&\\&=&(b-a)a+\displaystyle\frac{b-a}{n}\displaystyle\frac{b-a}{n}\displaystyle\frac{n(n+1)}{2}=ba-a^2+\displaystyle\frac{b^2-2ab+a^2}{2}\displaystyle\frac{n(n+1)}{n^2}\\&&\\\Rightarrow Z_{P_n}(f)&\overset{n\to\infty}{\longrightarrow}&ba-a^2+\displaystyle\frac{b^2}{2}-ab+\displaystyle\frac{a^2}{2}\;\;=\;\;\displaystyle\frac{b^2}{2}-\displaystyle\frac{a^2}{2}\end{array}\)
Das war allerdings etwas etwas mühsam!
Für stetige Funktionen gibt es zum Glück andere Methoden, das Riemann-Integral zu berechnen. Diese lernen wir im nächsten Abschnitt kennen.
