5.3a Berechnung der inversen Matrix
5.3 Die inverse Matrix (Fortsetzung)
Berechnung der inversen Matrix
Auch die inverse Matrix \(A^{-1}\) kann man mit einer Variante des Gaußschen Eliminationsverfahrens berechnen, die in diesem Zusammenhang auch oft Gauß-Jordan-Verfahren heißt.
Sei dazu \(B=(\vec{b}_1,\vec{b}_2,\ldots ,\vec{b}_ n)\) eine \(n\times n\)-Matrix, die wir uns aus \(n\) Spaltenvektoren zusammengesetzt vorstellen. Dann besteht die Matrix \(AB\) aus den \(n\) Spaltenvektoren \(A\vec{b}_1,A\vec{b}_2,\ldots ,A\vec{b}_ n.\) Da \(AB=E_ n\) ergeben soll, erhält man durch Vergleich der Spaltenvektoren, dass
\(A\vec{b}_j=\vec{e}_j\;\;\text{für}\;\;j=1,2,\ldots,n\)
sein muss. Um die Spalten der Matrix \(B\) zu bestimmen, muss man also jeweils ein Lineares Gleichungssystem lösen. Der "Trick" besteht nun darin, diese n linearen Gleichungssysteme alle gleichzeitig zu bearbeiten, indem man die rechten Seiten nebeneinanderschreibt. Da diese rechten Seiten gerade die Einheitsvektoren sind, steht rechts nun statt einem einzelnen Vektor die Einheitsmatrix \(E_n\) und links wie gewohnt die Matrix \(A\). Dann führt man solange elementare Zeilenoperationen durch, bis auf der linken Seite die Einheitsmatrix steht. Die Matrix, die sich dann rechts ergibt, ist gerade \(A^{-1}\).
Schematisch kann man folgendermaßen vorgehen und der Reihe nach auf der linken Seite die nötigen Einträge 1 und 0 erzeugen:
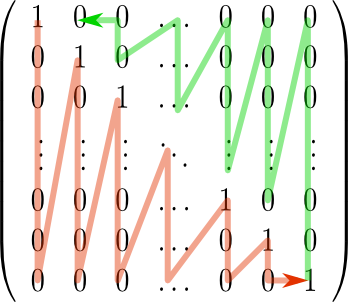
Indem man gegebenfalls zwei Zeilen vertauscht und die erste Zeile mit einer Zahl multipliziert sorgt man dafür, dass der linke obere Eintrag eine Eins ist. Durch Addition von Vielfachen der ersten Zeile kann man dann alle weiteren Einträge in der ersten Spalte zu Null machen. Man fährt dann mit der zweiten Spalte fort und erzeugt dort auf der Diagonalen eine Eins und darunter lauter Nullen usw. bis man links eine Matrix stehen hat, die auf der Diagonale nur Einsen und unterhalb der Diagonale nur Nullen hat. Anschließend arbeitet man sich von der letzten Spalte aus nach links und sorgt dafür, dass auch oberhalb der Diagonalen noch lauter Nullen stehen. Auf diese Weise gelangt man links zur Einheitsmatrix. Wenn man sauber gerechnet hat und auf der rechten Seite jeweils dieselben Zeilenoperationen durchführt, dann steht am Ende rechts die inverse Matrix \(A^{-1}\).
In der Praxis kann es sinnvoll sein, auf der Diagonale zunächst keine Einsen, sondern nur von Null verschiedene Einträge zu erzeugen, damit man so lange wie möglich mit ganzen Zahlen statt mit Brüchen rechnen kann. Die Diagonaleinträge kann man dann am Ende noch auf Eins normieren, wenn die Gefahr, sich zu verrechnen, wesentlich geringer ist.
\(A^{-1}=\displaystyle\frac{1}{a_{11}a_{22}-a_{12}a_{21}}\left(\begin{array}{rr}a_{22}&-a_{12}\\-a_{21}&a_{11}\end{array}\right)\)
Wenn wir demnächst noch die Determinante \(\det (A)=a_{11}a_{22}-a_{12}a_{21}\) als Abkürzung für den Nenner des hier auftretenden Bruchs kennengelernt haben, dann lässt sich dies noch kürzer in der Form
\(A^{-1}=\displaystyle\frac{1}{\det(A)}\left(\begin{array}{rr}a_{22}&-a_{12}\\-a_{21}&a_{11}\end{array}\right)\)
schreiben, oder in Worten:
-
Vertausche die Hauptdiagonalelemente
-
ändere die Vorzeichen auf der Nebendiagonalen und
-
teile durch die Determinante
Am besten probierst Du das direkt mal an einem Beispiel aus:
\(R_{\alpha}=\left(\begin{array}{rr}\cos(\alpha)&-\sin(\alpha)\\\sin(\alpha)&\cos(\alpha)\end{array}\right)\)
beschrieben. Eine solche Matrix heißt daher auch Drehmatrix. Mit Hilfe des Gauß-Jordan-Verfahrens bestimmt man die inverse Matrix:\(\begin{array}{rrr|rrr} \cos(\alpha)&-\sin(\alpha)&&&1&0\\ \sin(\alpha)&\cos(\alpha)&&&0&1\\ &&&&&\\ 1&-\displaystyle\frac{\sin(\alpha)}{\cos(\alpha)}&&&\displaystyle\frac{1}{\cos(\alpha)}&0\\ \sin(\alpha)&\cos(\alpha)&&&0&1\\ &&&&&\\ 1&-\displaystyle\frac{\sin(\alpha)}{\cos(\alpha)}&&&\displaystyle\frac{1}{\cos(\alpha)}&0\\ 0&\underbrace{\cos(\alpha)+\displaystyle\frac{\sin^2(\alpha)}{\cos(\alpha)}}_{=\frac{1}{\cos(\alpha)}}&&&-\displaystyle\frac{\sin(\alpha)}{\cos(\alpha)}&1\\ &&&&&\\ 1&-\displaystyle\frac{\sin(\alpha)}{\cos(\alpha)}&&&\displaystyle\frac{1}{\cos(\alpha)}&0\\ 0&1&&&-\sin(\alpha)&\cos(\alpha)\\ &&&&&\\ 1&0&&&\displaystyle\frac{1}{\cos(\alpha)}-\displaystyle\frac{\sin^2(\alpha)}{\cos(\alpha)}&\displaystyle\frac{\sin(\alpha)}{\cos(\alpha)}\cos(\alpha)\\ 0&1&&&-\sin(\alpha)&\cos(\alpha)\\ &&&&&\\ 1&0&&&\cos(\alpha)&\sin(\alpha)\\ 0&1&&&-\sin(\alpha)&\cos(\alpha) \end{array}\)
Damit ist\(\left(\begin{array}{rr}\cos(\alpha)&-\sin(\alpha)\\\sin(\alpha)&\cos(\alpha)\end{array}\right)^{-1}=\left(\begin{array}{rr}\cos(\alpha)&\sin(\alpha)\\-\sin(\alpha)&\cos(\alpha)\end{array}\right)=\left(\begin{array}{rr}\cos(-\alpha)&-\sin(-\alpha)\\\sin(-\alpha)&\cos(-\alpha)\end{array}\right)\)
Dies entspricht der anschaulichen Tatsache, dass die Drehung um den Winkel \(-\alpha\) die Umkehrung der Drehung um den Winkel \(\alpha\) darstellt.