12.4 Höhere Ableitungen

Die Ableitung einer Funktion lässt sich meist selbst noch einmal differenzieren. Diese "Ableitung der Ableitung" einer Funktion f nennt man dann die zweite Ableitung von f.

Definition (zweimal differenzierbar):

Sei \((a,b)\subset \mathbb {R}\) ein Intervall. Die Funktion \(f\colon(a,b)\to \mathbb {R}\) heißt zweimal differenzierbar, wenn die Ableitung \(f’\) von \(f\) ebenfalls eine differenzierbare Funktion ist. Wir schreiben dann \(f”\) für \((f’)’\) und nennen \(f”\) die zweite Ableitung von \(f\).

Analog ist \((f'')’=f'''\) die dritte Ableitung von \(f\) erklärt, wenn \(f”\) differenzierbar ist, usw.
Weil es irgendwann unpraktisch wird, die \(k\)-te Ableitung durch \(k\) Striche zu notieren, schreibt man bei höheren Ableitungen auch oft \(f^{(k)}\) für die \(k\)-te Ableitung.

Die zweite Ableitung hat auch eine konkrete geometrische Bedeutung. Dafür brauchen wir aber noch eine Definition.

Definition (konkav, konvex):
Sei \(f\colon(a,b)\rightarrow \mathbb {R}\) eine differenzierbare Funktion.

  • \(f\) heißt konkav (rechtsgekrümmt) auf \(( a,b)\) genau dann, wenn \(f’\) auf \(( a,b)\) monoton fallend ist.

  • \(f\) heißt konvex (linksgekrümmt) auf \((a,b)\) genau dann, wenn \(f’\) auf \((a,b)\) monoton wachsend ist.

"Rechtsgekrümmt" bzw. "linksgekrümmt" beschreibt die Gestalt des Graphen. Man stelle sich dazu vor, dass man mit einem (punktförmigen) Auto in Richtung der \(x\)-Achse auf dem Schaubild entlangbraust. Rechts bzw. links bezieht sich dann darauf, in welche Richtung man das Lenkrad einschlagen muss.

konvex

Satz :
Es sei \(f\colon(a,b)\to \mathbb {R}\) differenzierbar. Dann gilt:

  • \(f\) ist konkav auf \((a,b) \Leftrightarrow f( y)\leq f(x) +(y-x)\cdot f’( x)\;\;\) für alle \(\;\;x,y\in (a,b)\).

  • \(f\) ist konvex auf \((a,b) \Leftrightarrow f( y)\geq f( x) +(y-x)\cdot f’( x)\;\;\) für alle \(\;\;x,y\in (a,b)\).

Die beiden Ungleichungen haben eine sehr anschauliche geometrische Bedeutung: Wenn \(f( y)\leq f( x)+(y-x)\cdot f’( x)\) ist, dann liegen alle Punkte \((y,f( y))\) auf dem Schaubild von \(f\) unterhalb der Tangente an \(f\) im Punkt \(x\).

Figures/konvex_anschaulich

Satz:
Ist \(f\colon(a,b)\rightarrow \mathbb {R}\) zweimal differenzierbar, dann gilt:

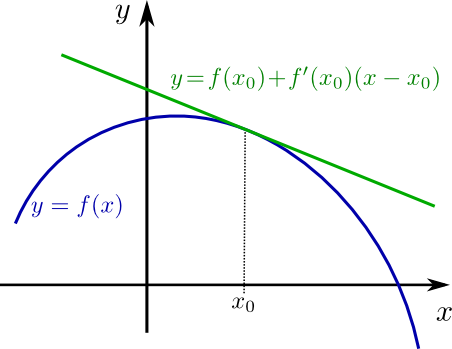
  • \(f\) ist konkav auf \((a,b) \Leftrightarrow \ f”( x)\leq 0\;\;\) für alle \(\;\;x\in (a,b)\).

  • \(f\) ist konvex auf \((a,b) \Leftrightarrow \ f”( x)\geq 0\;\;\) für alle \(\;\;x\in (a,b)\).

Beispiele:

  1. Die Funktionen \(f\) und \(g\) mit \(f( x)=\ln ( x)\) und \(g( x)=-x^{2}\) sind konkav.

  2. Die Funktionen \(f\) und \(g\) mit \(f( x)=\exp ( x)\) und \(g( x)=x^{2}\) sind konvex.

Definition (Wendepunkt):
Es sei \(f\colon(a,b)\rightarrow \mathbb {R}\) differenzierbar und \(x_{0}\in (a,b)\). Dann hat \(f\) in \(x_{0}\) einen Wendepunkt (oder: \(x_{0}\) ist eine Wendestelle von \(f\)) genau dann, wenn ein \(\varepsilon >0\) existiert mit einer der beiden folgenden Eigenschaften:

  • \(f\) ist auf \((x_{0}-\varepsilon ,x_{0})\) konvex und \(f\) ist auf \((x_{0},x_{0}+\varepsilon )\) konkav

  • \(f\) ist auf \((x_{0}-\varepsilon ,x_{0})\) konkav und \(f\) ist auf \((x_{0},x_{0}+\varepsilon )\) konvex.

Satz:
Ist \(f\colon (a,b)\rightarrow \mathbb {R}\) genügend oft differenzierbar, \(x_{0}\in (a,b)\), so hat \(f\) in \(x_0\) einen Wendepunkt wenn

  • \(f”( x_0)=0\) ist, und \(f”\) in \(x_0\) das Vorzeichen wechelt.

  • \(f”(x_0)=0\) und \(f^{(3)}(x_0) \neq 0\) ist.

Weiter zur Feedback-Seite
Ohne Test weiter zu Kapitel 13
Zuletzt geändert: Sonntag, 27. Januar 2019, 22:25