3.3 Darstellung von Ebenen

Ganz ähnlich wie eine Gerade durch einen Punkt und einen Richtungsvektor oder durch zwei Punkte festgelegt ist, kann man auch eine Ebene durch einen Punkt und zwei Richtungsvektoren oder durch drei Punkte beschreiben.

Als erstes betrachten wir eine Ebene, die den Punkt \(A\) enthält und von zwei nicht parallelen Vektoren \(\vec{u}\) und \(\vec{v}\) erzeugt wird.

Ein Punkt \(X\) liegt in dieser Ebene, wenn der Vektor \(\overrightarrow {AX}\) darstellbar ist als

\(\overrightarrow{AX}=s\cdot\vec{u}+t\cdot\vec{v}\)

mit geeigneten \(s,t\in \mathbb {R}\).

Dies ist die Parameterdarstellung von \(E\).

In kartesischen Koordinaten lautet die Ebenengleichung dann

\(\left(\begin{array}{r}x_1\\x_2\\x_3\end{array}\right)=\left(\begin{array}{r}a_1\\a_2\\a_3\end{array}\right)+s\cdot\left(\begin{array}{r}u_1\\u_2\\u_3\end{array}\right)+t\cdot\left(\begin{array}{r}v_1\\v_2\\v_3\end{array}\right)\)

Falls eine Ebene \(E\) durch drei Punkte \(A\), \(B\), \(C\) festgelegt wird, kann man als Richtungsvektoren \(\vec{u}= \overrightarrow {AB}\) und \(\vec{v}= \overrightarrow {AC}\) wählen.
Ein Punkt \(X\) liegt in der Ebene, wenn der Vektor \(\overrightarrow {AX}\) darstellbar ist als

\(\overrightarrow{AX}=s\cdot\overrightarrow{AB}+t\cdot\overrightarrow{AC}\)

mit geeigneten \(s,t\in \mathbb {R}\). Man erhält dann die Drei-Punkte-Form der Ebenengleichung

\(E:\left(\begin{array}{r}x_1\\x_2\\x_3\end{array}\right)=\left(\begin{array}{r}a_1\\a_2\\a_3\end{array}\right)+s\cdot\left(\begin{array}{r}b_1-a_1\\b_2-a_2\\b_3-a_3\end{array}\right)+t\cdot\left(\begin{array}{r}c_1-a_1\\c_2-a_2\\c_3-a_3\end{array}\right)\)

Es gibt noch weitere Möglichkeiten, Ebenen durch Gleichungen darzustellen. Wenn die Ebene \(E\) durch die drei Punkte \(A\), \(B\) und \(C\) verläuft, dann liegt ein Punkt \(X\) genau dann in dieser Ebene, wenn die drei Vektoren \(\overrightarrow {AX}\),\(\overrightarrow {AB}\) und \(\overrightarrow {AC}\) linear abhängig sind. Dies kann man wiederum mit Hilfe des Spatprodukts sehr kompakt ausdrücken:

\([\overrightarrow{AX},\overrightarrow{AB},\overrightarrow{AC}]=\overrightarrow{AX}\cdot(\overrightarrow{AB}\times\overrightarrow{AC})=0\)

Der Vektor \(\vec{n}=\overrightarrow {AB}\times \overrightarrow {AC}\) steht senkrecht auf \(E\) und heißt Normalenvektor von \(E\).

Mit seiner Hilfe kann man eine besonders knappe Form der Ebenengleichung angeben.

In kartesischen Koordinaten mit \(A=(a_1,a_2,a_3)\) und \(\vec{n}=\left(\! \begin{array}{r}n_1\\ n_2\\ n_3\end{array}\! \right)\) lautet die Normalengleichung

\(n_1x_1+n_2x_2+n_3x_3=C\;\;\;\) mit \(\;\;C=n_1a_1+n_2a_2+n_3a_3.\)

Abstände und Schnittwinkel von Ebenen

Wenn es um Abstände von Ebenen zu Punkten, Geraden oder anderen Ebenen geht, sind folgende Grundaufgaben zu lösen:

1. Abstand eines Punktes von einer Ebene

2. Abstand einer Geraden von einer Ebene

3. Abstand zwischen zwei parallelen Ebenen

4. Schnittwinkel zwischen Gerade und Ebene

5. Schnittwinkel zwischen zwei Ebenen

Zunächst sollte man sich klarmachen, dass es genügt, den Abstand eines Punktes von einer Ebene berechnen zu können, um auch die beiden nächsten Aufgaben zu lösen. Eine Gerade und eine Ebene können im \(\mathbb {R}^3\) nur drei Lagen relativ zueinander einnehmen, entweder die Gerade liegt in der Ebene, oder sie schneidet die Ebene in einem Punkt oder die Gerade ist parallel zur Ebene. Nur im letzten Fall kann man von einem echten Abstand sprechen und dieser ist von jedem Punkt der Geraden zur Ebene gleich. Man kann also den Abstand wieder bestimmen, indem man einen beliebigen Punkt der Geraden auswählt und seinen Abstand zur Ebene berechnet.

Ähnlich übersichtlich ist die Lage bei zwei parallelen Ebenen. Auch hier hat jeder Punkt der einen Ebene denselben Abstand zur anderen Ebene und kann folglich verwendet werden, um den Abstand der beiden Ebenen zu berechnen.

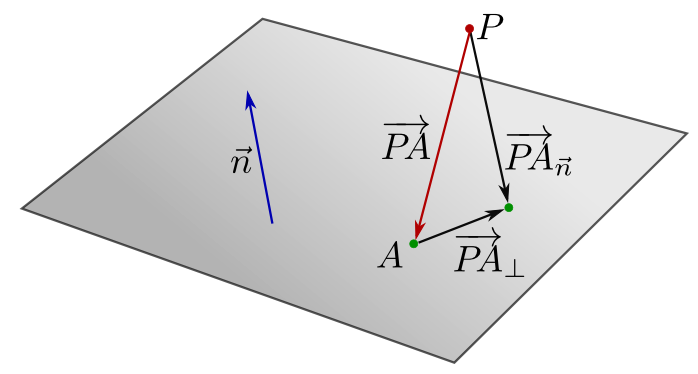
Der Abstand eines Punktes \(P\) von einer Ebene berechnet sich wieder dadurch, dass man den Verbindungsvektor von \(P\) zu einem beliebigen Punkt \(A\) der Ebene in einen Anteil in Richtung von \(\vec{n}\) sowie einen Anteil senkrecht dazu zerlegt. Der Abstand von \(P\) zur Ebene ist dann gerade die Länge des zu \(\vec{n}\) parallelen Anteils.

Mit der orthogonalen Zerlegung

\(\overrightarrow{PA}_{\vec{n}}=\displaystyle\frac{\overrightarrow{PA}\cdot\vec{n}}{|\vec{n}|^2}\,\vec{n}\)

ergibt sich als Abstand \(d\) des Punktes \(P\) von der Ebene daher

\(d=|\overrightarrow{PA}_{\vec{n}}|=\displaystyle\frac{|\overrightarrow{PA}\cdot\vec{n}|}{|\vec{n}|}\)

Im Fall \(|\vec{n}|=1\) ist also \(d= |\overrightarrow {PA}\cdot \vec{n}|\).

Schnitte von Ebenen und Geraden

Im \(\mathbb {R}^3\) gibt es drei Möglichkeiten, wie zwei Ebenen \(E_1\) und \(E_2\) relativ zueinander liegen können:

1. die Ebenen sind identisch

2. die Ebenen sind nicht identisch, aber parallel zueinander

3. die Ebenen schneiden sich entlang einer Geraden

Im letzten Fall steht man vor der Aufgabe, den Schnitt der beiden Ebenen zu bestimmen. Wenn \(\vec{n}_1\) ein Normalenvektor von \(E_1\) und \(\vec{n}_2\) ein Normalenvektor von \(E_2\) ist, so ist das Kreuzprodukt \(\vec{n}_1\times \vec{n}_2\) senkrecht zu \(\vec{n}_1\) und damit parallel zu \(E_1\). Aus demselben Grund ist \(\vec{n}_1\times \vec{n}_2\) auch parallel zu \(E_2\). Der Vektor \(\vec{n}_1\times \vec{n}_2\) ist daher ein Richtungsvektor der Schnittgeraden von \(E_1\) und \(E_2\). Wenn man noch einen Punkt \(A\) auf \(\)g\(\) bestimmt, so kann man die Punkt-Richtungsform der Schnittgeraden angeben.

Schnittwinkel von Ebenen

Der Winkel zwischen zwei sich schneidenden Ebenen ist definiert als der Winkel, den die beiden Normalenvektoren einschließen:

\(\cos(\varphi)=\displaystyle\frac{|\vec{n}_1{\cdot}\vec{n}_2|}{|\vec{n}_1|\cdot|\vec{n}_2|}\)

Dies ist übrigens der kleinste Winkel, den man zwischen zwei Vektoren erhalten kann, von denen jeweils einer zu einer der beiden Ebenen parallel ist.

Der Winkel zwischen einer Geraden mit Richtungsvektor \(\vec{c}\) lässt sich ebenfalls über den Normalenvektor \(\vec{n}\) der Ebene berechnen. Allerdings ist der Winkel \(\alpha \) zwischen \(\vec{c}\) und \(\vec{n}\) nicht der gesuchte Winkel, sondern der Schnittwinkel ist \(\frac{\pi }{2}-\alpha \).

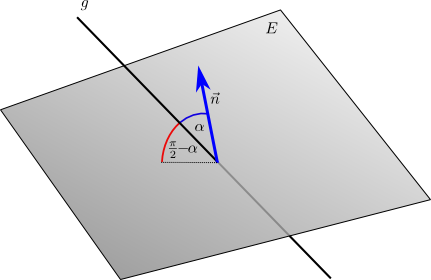
Unter Berücksichtigung der Beziehung \(\cos (\frac{\pi }{2}- x)=\sin ( x)\) gilt daher für den Schnittwinkel \(\varphi \):

\(\sin(\varphi)=\displaystyle\frac{|\vec{c}\cdot\vec{n}|}{|\vec{c}|\cdot|\vec{n}|}\)