8.2. Quadriken im $\mathbb{R}^2$
8.2. Quadriken im \(\mathbb{R}^2\)
Jedes allgemeine quadratische Polynom
\(q(x_1,x_2)=(x_1,x_2)\left(\begin{array}{rr}a_{11}&a_{12}\\ a_{12}&a_{22}\end{array}\right)\left(\begin{array}{r}x_1\\x_2\end{array}\right)+ (a_1,a_2)\cdot\left(\begin{array}{r}x_1\\x_2\end{array}\right)+\alpha\)
in zwei Variablen \(x_1\) und \(x_2\) kann auf eine der im vorigen Abschnitt beschriebenen Normalformen gebracht werden.
Die folgenden Möglichkeiten können dabei eintreten:
-
\(\mathrm{Rang}\, (A)=2\):
in diesem Fall sind beide Eigenwerte \(\lambda _{1,2}\) von \(A\) von Null verschiedene reelle Zahlen und die linearen Terme lassen sich durch quadratisches Ergänzen entfernen.Ohne Einschränkung kann man die Vorzeichen immer so wählen, dass der Term mit \(x_1^2\) positiv ist. Außerdem kann man immer durch den konstanten Term teilen, so dass dieser Damit ergeben sich die folgenden Normalformen
\(\begin{array}{rcl}\displaystyle\frac{x_1^2}{c^2}+\displaystyle\frac{x_2^2}{d^2}-1&=&0\;\;\;\;\text{Ellipse, bzw. Kreis, falls}\;\;c=d\\ \displaystyle\frac{x_1^2}{c^2}+\displaystyle\frac{x_2^2}{d^2}+1&=&0\;\;\;\;\text{leere Menge}\\ \displaystyle\frac{x_1^2}{c^2}-\displaystyle\frac{x_2^2}{d^2}-1&=&0\;\;\;\;\text{Hyperbel}\\ \displaystyle\frac{x_1^2}{c^2}+{x_2^2}&=&0\;\;\;\;\text{einzelner Punkt}\\ \displaystyle\frac{x_1^2}{c^2}-{x_2^2}&=&0\;\;\;\;\text{zwei sich schneidende Geraden}\end{array}\)
-
\(\mathrm{Rang}\, (A)=1\):
In diesem Fall ist einer der Eigenwerte Null und einer von Null verschieden. Ohne Einschränkung können wir annehmen, dass \(\lambda _1\neq 0\) und \(\lambda _2=0\) ist und dass in der Normalform der Term mit \(x_1^2\) wieder positiv ist.\(\begin{array}{rcl}\lambda_1x_1^2+c_2x_2+\beta&=&0\;\;\;\;\text{Parabel, falls }c_2\neq 0\\ \displaystyle\frac{x_1^2}{c^2}+1&=&0\;\;\;\;\text{leere Menge}\\ \displaystyle\frac{x_1^2}{c^2}-1&=&0\;\;\;\;\text{zwei parallele Geraden}\\ \displaystyle\frac{x_1^2}{c^2}&=&0\;\;\;\;\text{eine Gerade}\end{array}\)
-
\(\mathrm{Rang}\, (A)=0\):
In diesem Fall müssen beide Eigenwerte von \(A\) verschwinden und \(A\) muss in diesem Fall die Nullmatrix sein. Die Funktion ist also gar keine "‘quadratische Funktion"’, daher können wir diesen Fall ignorieren.
\(q(x,y)=5\,x^2+4\,xy+8\,y^2+\displaystyle\frac{14\sqrt{5}}{5}\,x-\displaystyle\frac{52\sqrt{5}}{5}\,y-11=0\)
gegeben ist, schreiben wir \(q\) zunächst um in die Form\(q(x,y)=\left(\begin{array}{r}x\\y\end{array}\right)^T\left(\begin{array}{rr}5&2\\2&8\end{array}\right)\left(\begin{array}{r}x\\y\end{array}\right)+(\frac{14\sqrt{5}}{5}\;-\frac{52\sqrt{5}}{5})\left(\begin{array}{r}x\\y\end{array}\right)-11\)
und bestimmen die Eigenwerte der symmetrischen Matrix \(A=\left(\begin{array}{rr}5& 2\\ 2& 8\end{array}\right)\). Mit dem charakteristischen Polynom\(\chi_A(\lambda)=\det(A-\lambda\,E_n)=(5-\lambda)(8-\lambda)-2^2=\lambda^2-13\lambda+36\)
ergeben sich die Eigenwerte \(\lambda _1=4\) und \(\lambda _2=9\) mit Eigenvektoren\(v_1=\left(\begin{array}{r}2\\-1\end{array}\right),\;\;\;\;v_2=\left(\begin{array}{r}1\\2\end{array}\right)\)
Diese stehen automatisch senkrecht aufeinander, haben aber noch nicht die Länge \(1\). Eine orthogonale Matrix, die die Matrix \(A\) diagonalisiert, ist daher\(T=\frac{1}{\sqrt{5}}\left(\begin{array}{rr}2&1\\-1&2\end{array}\right)\)
Mit \(\vec{y}= T^ T \vec{x}\) beziehungsweise \(\vec{x}= T \vec{y}\) erhält man daraus\(\tilde{q}(y_1,y_2)=4y_1^2+9y_2^2+16y_1-18y_2-11=4(y_1^2+4y_1)+9(y_2^2+2y_2)-11\)
und durch quadratisches Ergänzen, indem man \(z_1=y_1+2\) und \(z_2=y_2+1\) setzt schließlich\(\hat{q}(z_1,z_2)=4z_1^2+9z_2^2-36.\)
Damit ist\(\hat{q}(z_1,z_2)=0\;\;\Leftrightarrow\;\;\displaystyle\frac{z_1^2}{3^2}+\displaystyle\frac{z_2^2}{2^2}-1=0\)
es handelt sich also um eine Ellipse mit Halbachsen \(r_1=3\) und \(r_2=2\), die gedreht und verschoben im ursprünglichen Koordinatensystem liegt.
Die folgende Skizze veranschaulicht, wie die Quadrik aus einer "‘normal"’ im Koordinatensystem liegenden Ellipse durch Drehen und Verschieben entsteht.
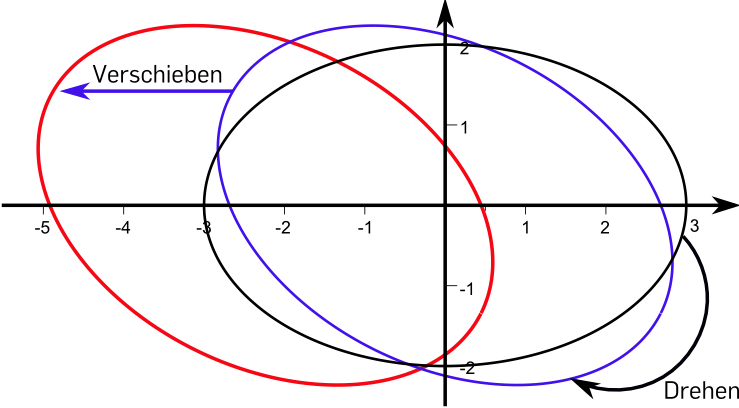
Geogebra-Applet: Quadriken in der Ebene
Versuchen Sie Werte zu finden, bei denen ein Kreis, eine Ellipse, eine Hyperbel und eine Parabel auftritt.
