1.1 Mengen
Mengen sind einer der grundlegendsten Begriffe in der Mathematik. Sie sind so grundlegend, dass wir (hoffentlich) nach kurzer Zeit gar nicht mehr daran denken werden, wenn wir mit Mengen arbeiten. Unter einer Menge versteht man die gedankliche Zusammenfassung von verschiedenen Objekten. Diese Objekte nennt man die Elemente der Menge. Mengen kann man angeben, indem man ihre Elemente aufzählt oder indem man die Elemente charakterisiert.
\(A=\{a;a\text{ hat die Eigenschaft }E\}.\)
Wenn ein Objekt \(a\) zur Menge \(A\) gehört, schreiben wir \(a\in A\), ansonsten \(a\notin A\).
Beispielsweise ist $K=\{ 2,3,4,5,6\}$ eine Menge, aber auch
\(L=\{n\in\mathbb{N};\;n\text{ ist kleiner als }10\text{ und durch }3\text{ teilbar}\}=\{3,6,9\}.\)
Recht anschaulich ist die Vorstellung einer Menge als ein "‘Behälter"’ für darin enthaltene unterscheidbare Objekte. Die Elemente sind auch nicht sortiert, d.h<active::~> die beiden Mengen \(\{ 3,6,9\} \) und $\{ 9,3,6\}$ sind gleich. Es kann auch sein, dass der Behälter keine Gegenstände enthält. Eine solche Menge ohne Elemente nennt man die leere Menge, geschrieben \(\{ \} \) oder $\emptyset$. Die leere Menge ist also nicht "‘Nichts"’, sondern kann als ein Behälter ohne Inhalt aufgefasst werden.
Aus zwei Mengen \(A\) und \(B\) kann man auf verschiedene Arten weitere Mengen konstruieren:
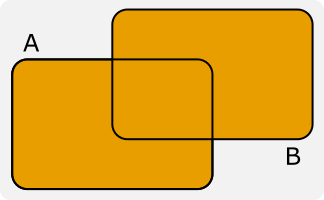
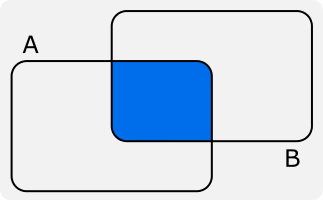
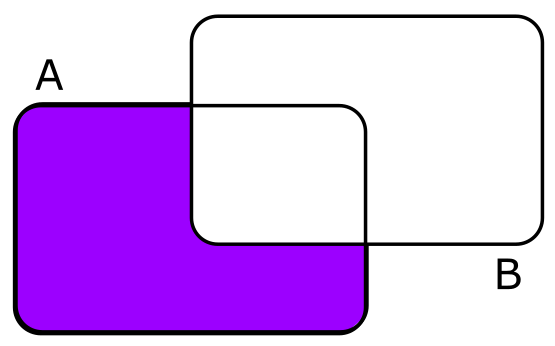
\(\begin{array}{rcl}K\cup L&= &\{2,3,4,5,6,9\},\\K \cap L&=&\{3,6\}\text{ und }\\ K\setminus L&=&\{2,4,5\}\end{array}\)
Achtung! In der Mathematik bedeutet "‘in A oder B enthalten"’ nicht "‘entweder in A oder in B enthalten"’, sondern es schließt die Möglichkeit "‘in A und B enthalten"’ mit ein.
Hier noch eine kleine Testaufgabe dazu:
Durch die Kombination von verschiedenen Operationen kann man weitere Mengen darstellen.
