1.1 Mengen (Fortsetzung 3)
Bei der Vereinigung, Durchschnittsbildung und der Differenz von Mengen gibt es einige Regeln zu beachten.
Rechenregeln für Mengen
Aus der Definition von Vereinigungen und Durchschnitten ergibt sich, dass für zwei Mengen A und B gilt:
\( A\,{\cup}\,B =B\,{\cup}\,A \;\text{ und }\; A\,{\cap}\,B =B\,{\cap}\,A\;\;\) (Kommutativgesetze)
\( (A\cup B) \cup C\,=\,A \cup (B \cup C)\;\) und \(\; (A \cap B) \cap C\,=\,A \cap (B \cap C)\;\;\)
(Assoziativgesetze)
Es kommt also nicht darauf an, in welcher Reihenfolge man Vereinigungen und Durchschnitte aufschreibt oder wie man Klammern setzt, solange in einem Ausdruck nur Vereinigungen oder nur Durchschnitte vorkommen.
Anders ist es bei der Mengendifferenz. Hier gilt im allgemeinen \((A\setminus B)\setminus C\neq A\setminus(B\setminus C)\).
Klammern werden auch dann wichtig, wenn man Ausdrücke betrachtet, die Vereinigungen, Durchschnitte und Mengendifferenzen enthalten.
Hier gelten zum Beispiel die
Für Teilmengen \(A,B\,\subseteq\,M\) einer Menge M gilt:
\(\begin{array}{rcl} M\setminus(A\,\cap\,B)&=&(M\setminus A) \cup (M\setminus B)\\ M\setminus(A\,\cup\,B)&=&(M\setminus A)\,\cap\,(M\setminus B)\end{array}\)
Die Gültigkeit dieser Regeln kann man sich auf verschiedene Arten klarmachen:
-
durch einen logisch korrekten, formalen mathematischen Beweis (die einzige Art, die Mathematiker wirklich gelten lassen), aber für unsere Zwecke etwas aufwändig.
-
durch eine überzeugende Skizze
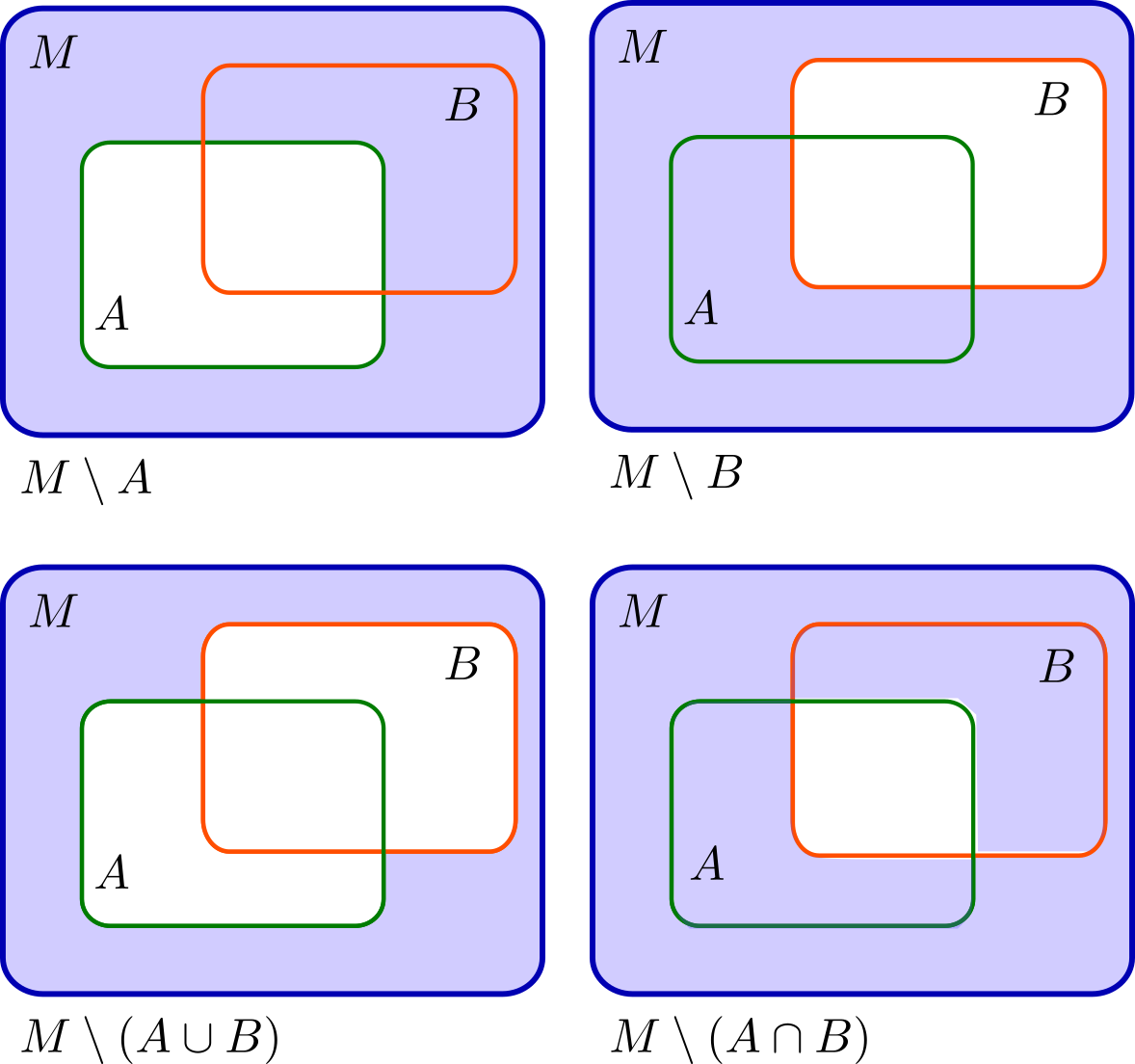
Die De Morganschen Regeln lassen sich folgendermaßen aus diesen Skizzen ablesen: Die im unteren linken Bild blau schraffierten Punkte sind genau die Punkte, die in einem der oberen beiden Bilder (oder in beiden) blau schraffiert sind, während die unten rechts blau schraffierten Punkte genau diejenigen Punkte sind, die in beiden oberen Bildern blau schraffiert sind.
Mathematiker tun sich mit solchen "‘anschaulichen"’ Argumenten manchmal etwas schwer, weil nicht immer sofort klar ist, dass man auch wirklich genau die Aussage der Regeln in ein Bild übersetzt und nicht beispielsweise nur einen Spezialfall betrachtet.
-
indem man sich ein Beispiel überlegt, das einen von der Allgemeingültigkeit der Aussage überzeugt.
Die Mengen könnten beispielsweise sein:
M = \(\{ \) alle Veranstaltungen der nächsten Woche in Bochum\(\} \)
A = \(\{ \) alle Veranstaltungen am nächsten Dienstag in Bochum\(\} \)
B = \(\{ \) alle Veranstaltungen der nächsten Woche in Bochum, die um 20 Uhr beginnen\(\} \)Dann übersetzt sich die erste Regel von De Morgan in
\(M\setminus (A\cap B)\) = Veranstaltungen in Bochum, die nicht am Dienstag um 20 Uhr beginnen
= Veranstaltungen, die nicht am Dienstag stattfinden oder nicht um 20 Uhr beginnenwobei das oder wie oben bereits erwähnt in der Mathematik nicht entweder…oder bedeutet, sondern auch beide Möglichkeiten wahr sein können.
Für die zweite Regel wählen wir andere Mengen:
M = Studierende der Ruhr-Uni
A= VWL-Studierende an der Ruhr-Uni
B = Philosophie-Studierende an der Ruhr-Uni
-
Dann besagt die zweite De Morgansche Regel in Worten:
Ein Studierender, der nicht VWL studiert (\(M\setminus A\)) und der nicht Philosophie studiert (\(M\setminus B\)), gehört zu den Studierenden, die weder VWL noch Philosophie studieren (\(M\setminus (A\,\cup\,B)\))
