1.6a Funktionen (Fortsetzung)
1.6 Funktionen (Fortsetzung)
Im Rest dieses Abschnitts lernen wir noch einige wichtige Grundbegriffe kennen, die im Zusammenhang mit Funktionen verwendet werden.
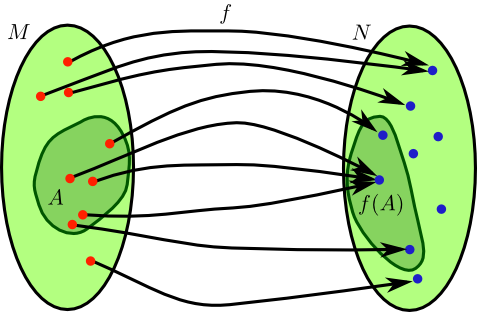
Sei \(f:M\to N\) eine Abbildung und \(A\subset M\) Teilmenge von \(M\).
Dann heißt \(\; \; f(A)= \{ f(a);\; a\in A\} \; \; \) das Bild von \(A\) unter \(f\).
Für \(f\colon\mathbb{R}\to \mathbb{R}\) mit \(f(x)=x^2\) ist
-
\( f(\mathbb {R})= [0,\infty )\)
-
\(f(\{ 2,3\} )= \{ 4,9\}\) aber auch \(f(\{ -3,2\} )= \{ 4,9\}\)
Es kann also durchaus mehrere verschiedene Mengen geben, die dasselbe Bild besitzen.
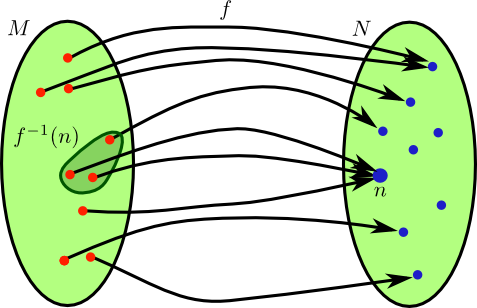
Sei \(f:M\to N\) eine Abbildung und \(n\in N\).
Dann ist das Urbild \(f^{-1}( n)= \{ m\in M;\; f( m)=n\} \) von \(n\) die Menge aller Elemente von \(M\), die auf \(n\) abgebildet werden.
Für \(f:\mathbb {R}\to \mathbb {R}\) mit \(f( x)=x^2\) ist
-
\(f^{-1}(2)=\{ +\sqrt {2}, -\sqrt {2}\} \) das Urbild von \(2\) und
-
\(f^{-1}(0)= \{ 0 \} \)
Sei \(f:M\to N\) eine Abbildung und \(B\subseteq N\) eine Teilmenge von \(N\).
Dann heißt die Menge aller Elemente von \(M\), die nach \(B\) abgebildet werden, das Urbild von \(B\):
\(f^{-1}(B)=\{m\in M;\;f( m)\in B\}\)
Beispiel: \(f( x)=x^2\) Für \(B=[4,9)\) ist \(f^{-1}(B)=[2,3)\cup (-3,-2]\).
