15.2 Kurven und ihre Länge
15.2 Kurven und ihre Länge
Eine sehr allgemeine Art, mit der man Kurven in der Ebene beschreiben kann, ist die Parameterdarstellung. Dabei durchläuft ein Parameter \(t\) ein Intervall \([a,b]\) während der durch zwei differenzierbare Funktionen \(x(t)\) und \(y(t)\) definierte Punkt \(P(t)=(x(t),y(t))\in \mathbb {R}^2\) sich in der Ebene stetig ändert. Man kann sich den Parameter \(t\) gut als Zeit vorstellen und die Kurve als Bahn eines Teilchens in der Ebene.
- Kreislinie
Ein Kreis mit Radius \(r\) und Mittelpunkt \((x_ M, y_ M)\) lässt sich durch
\(\left(\begin{array}{r}x(t)\\y(t)\end{array}\right)=\left(\begin{array}{r}x_M+r\cos(t)\\y_M+r\sin(t)\end{array}\right)\)
mit \(0\leq t{\leq }2\pi\) parametrisieren. Dies ist zwar nur eine von unendlich vielen möglichen Parametrisierungen, aber sicher die mit großem Abstand am häufigsten vorkommende. Interpretiert man diese Parameterdarstellung als Bahnkurve, so bewegt sich das Teilchen mit konstanter Geschwindigkeit.
- Ellipse
Eine Ellipse mit den Halbachsen \(a\) und \(b\), die durch die Gleichung \(\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1\) gegeben ist, lässt sich ähnlich wie der Kreis parametrisieren durch
mit \(0\leq t\leq 2\pi\). Dies ist zwar nur eine von unendlich vielen möglichen Parametrisierungen, aber sicher die mit großem Abstand am häufigsten vorkommende. Interpretiert man diese Parameterdarstellung als Bahnkurve, so bewegt sich das Teilchen mit konstanter Geschwindigkeit.\(\left(\begin{array}{r}x(t)\\y(t)\end{array}\right)=\left(\begin{array}{r}a\cos(t)\\b\sin(t)\end{array}\right)\) 
- Kardiodide
Auch durch
mit \(0\leq t{\leq }2\pi\) wird eine Kurve in der Ebene definiert. Diese heißt Herzkurve oder Kardiodide . Man beachte, dass diese Kurve eine "‘Spitze"’ besitzt, obwohl die Ausdrücke für \(x(t)\) und \(y(t)\) "glatt", d.h. differenzierbar sind.\(\left(\begin{array}{r}x(t)\\y(t)\end{array}\right)=\left(\begin{array}{r}a\cos(t)(1+\cos(t))\\a\sin(t)(1+\cos(t))\end{array}\right)\) 
Mt dem folgenden Applet können Sie selbst ausprobieren, wie man Kurven durch eine Parameterdarstellung erzeugen kann.
Geogebra-Applet: Parameterdarstellung von Kurven
\(\gamma(t)=\left(\begin{array}{r}x(t)\\y(t)\end{array}\right)\)
heißt regulär, wenn \(\dot{x}(t)\) und \(\dot{y}(t)\) stetige Funktionen sind, die nie gleichzeitig verschwinden, d.h.\(\dot{x}(t)^2+\dot{y}(t)^2 \neq 0\)
für alle \(t\).Man kann reguläre Kurven "‘ungeschickt"’ parametrisieren, so dass sie nicht mehr regulär sind. Es gibt jedoch auch Kurven, die in keiner Parametrisierung regulär sind, zum Beispiel die Neilsche Parabel
\(\left(\begin{array}{r}x(t)\\y(t)\end{array}\right)=\left(\begin{array}{r}t^2\\t^3)\end{array}\right)\)
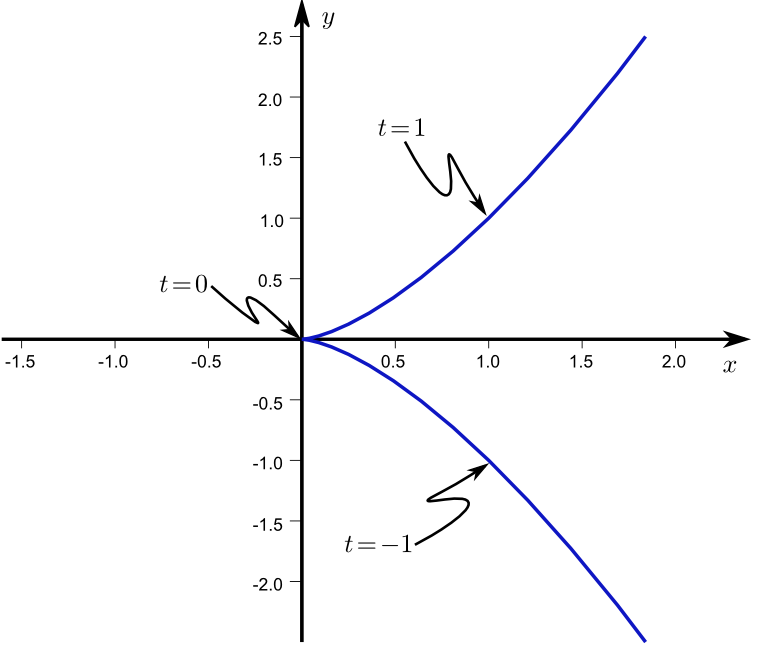
Diese Kurven wollen wir im folgenden Abschnitt nicht berücksichtigen.
Eine weitere Klasse von Kurven in der Ebene sind die Schaubilder von stetigen Funktionen.
| \(\left(\begin{array}{r}x(t)\\y(t)\end{array}\right)=\left(\begin{array}{r}t\\ft)\end{array}\right)\) |
Tangentenvektor
Stellt man sich \(\vec{c}(t)\) als Bahnkurve eines Teilchens vor, dann ist die momentane Geschwindigkeit die Ableitung \(\dot{\vec{c}}(t)\), die man komponentenweise bildet:
| \(\vec{t}(x)=\dot{\vec{c}}(t)=\left(\begin{array}{r}\dot{x}(t)\\\dot{y}(t)\end{array}\right).\) |
Dieser Vektor ist immer tangential an die Kurve und heißt Tangentenvektor. Seine Länge beschreibt die Momentangeschwindigkeit.
Wenn \(\vec{c}(t)\) eine reguläre Kurve beschreibt, dann ist \(\vec{t}(x)\neq \vec{0}\), d.h. die Geschwindigkeit ist immer positiv.
- Wenn \(\vec{c}(t)=\left(\!\!\begin{array}{r} \cos (t)\\ \sin (t)\end{array}\!\right)\) den Einheitskreis durchläuft, dann ist \(\vec{t}(x)=\left(\!\!\begin{array}{r} -\sin (t)\\ \cos (t)\end{array}\!\!\right)\) der Tangentenvektor im Punkt \(\vec{c}(t)\).
- Für die Ellipse mit \(\vec{c}(t)=\left(\!\!\begin{array}{r} a\cos (t)\\ b\sin (t)\end{array}\!\!\right)\) ist der Tangentenvektor \(\vec{t}(x)=\left(\!\!\begin{array}{r} -a\sin (t)\\ b\cos (t)\end{array}\!\!\right)\).
