13.1 Der Mittelwertsatz
Kapitel 13: Anwendungen der Differentiation
13.1 Der Mittelwertsatz
Dann existiert ein \(\xi \in (a,b)\) mit \(f’(\xi )=0\).
Beweis: Wir betrachten drei mögliche Fälle.
-
1. Möglichkeit: \(f\) ist eine konstante Funktion auf dem Intervall \([a,b]\)
\(\Rightarrow f’(\xi)=0\,\;\forall\xi\in(a,b)\)
-
2. Möglichkeit: Es gibt ein \(x_0\in (a,b)\) mit \(f( x_0)>f(a)=f(b)\) Nach dem Satz vom Maximum nimmt die stetige Funktion \(f\) auf dem kompakten Intervall \([a,b]\) ihr Maximum an, es existiert also ein \(\xi \in [a,b]\) mit \(f(\xi )\geq f( x)\, \forall x\in [a,b]\). Da \(\xi \in (a,b)\) und nicht am Rand des Intervalls \([a,b]\) liegt, ist \(\xi \) ein lokales Maximum. Wir wissen bereits, dass in einem Maximum die Ableitung verschwinden muss, also ist dann \(f’(\xi )=0\).
-
3. Möglichkeit: Es existiert ein \(x_0\in (a,b)\) mit \(f( x_0)<f(a)=f(b)\). Dann argumentiert man ähnlich wie im vorigen Fall, denn die stetige Funktion \(f\) nimmt auf dem kompakten Intervall \([a,b]\) ihr Minimum in einem Punkt \(\xi \) an. Dieser muss im offenen Intervall \((a,b)\) liegen und ist daher ein lokales Minimum. Also ist dort \(f’(\xi )=0\).
□
Aus dem Satz von Rolle folgt direkt ein wichtiger Satz der Analysis.
\(f’(\xi)=\displaystyle\frac{f(b)-f(a)}{b-a}.\)
Graphisch lässt sich die Aussage des Mittelwertsatzes so darstellen:
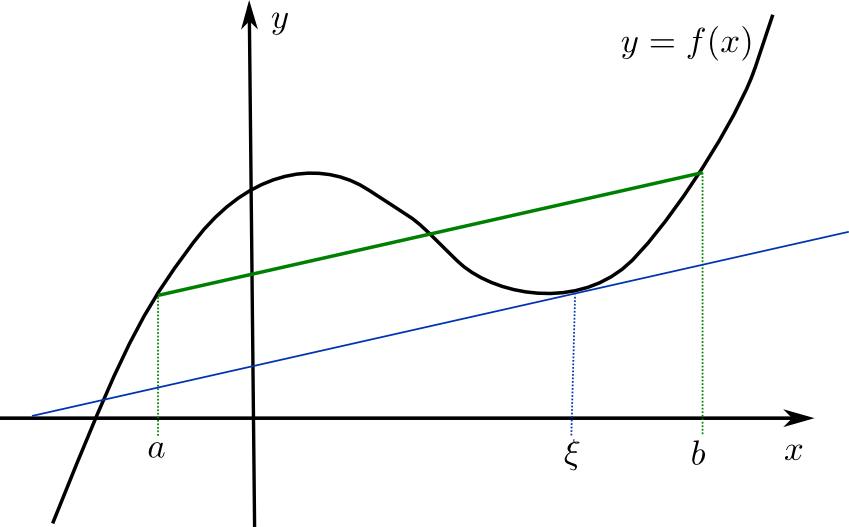
Die Tangentensteigung an der Stelle \(\xi \) ist genau die Steigung der Sehne, die die Punkte \((a,f(a))\) und \((b,f(b))\) miteinander verbindet.
Das folgende Geogebra-Applet erlaubt, die Ränder des Intervalls [a,b] zu verändern und durch Verschieben die richtige Lage des Punktes \(\xi\) herauszufinden.
Applet zum Mittelwertsatz - GeoGebra Dynamisches Arbeitsblatt
Die Punkte a, b und \(\xi\) lassen sich verschieben. Wenn die Tangente im Punkt \((\xi,f(\xi))\) die Bedingung des Mittelwertsatzes erfüllt, färbt sie sich grün.
Wenn man sich die \(x\)-Variable als eine Zeit und die Funktion \(f\) als die zurückgelegte Strecke vorstellt, dann ist \(\displaystyle\frac {f(b)-f(a)}{b-a}\) die Durchschnittsgeschwindigkeit zwischen den Zeitpunkten \(a\) und \(b\) und der Mittelwertsatz besagt, dass irgendwann zwischen diesen beiden Zeitpunkten die Momentangeschwindigkeit genau gleich der Durchschnittsgeschwindigkeit ist. Anschaulich ist das relativ klar, denn es kann ja nicht sein, dass die Momentangeschwindigkeit immer kleiner als die Durchschnittsgeschwindigkeit oder immer größer als die Durchschnittsgeschwindigkeit ist.
Wir belassen es aber nicht bei dieser anschaulichen Erklärung, sondern geben für den Mittelwertsatz auch einen formalen
Beweis:
Zunächst definieren wir eine Hilfsfunktion \(g:[a,b]\rightarrow \mathbb {R}\), die die Funktion \(f\) so "verbiegt", dass wir den Satz von Rolle anwenden können, und zwar durch
\(g(x):=f( x)-(x-a)\cdot\displaystyle\frac{f(b)-f(a)}{b-a}.\)
anschaulich entspricht das einer Scherung in \(y\)-Richtung, die dafür sorgt, dass die Sehne, die oben angesprochen wurde, zu einer horizontalen Geraden wird.
Die Funktion \(g\) ist stetig auf \([a,b]\) und differenzierbar auf \((a,b)\) mit den Werten
\(\begin{array}{rcl}g(a)&=&f(a)\;\;\text{ und }\\g(b)&=&f(b)-\displaystyle\frac{f(b)-f(a)}{b-a}(b-a)=f(a).\end{array}\)
Wir können also tatsächlich den Satz von Rolle anwenden. Nach diesem Satz existiert ein \(\xi \in (a,b)\) mit \(g’(\xi )=0\). An dieser Stelle \(\xi \) ist dann \(f’(\xi )-\displaystyle\frac {f(b)-f(a)}{b-a}=0\).
□
Wenn man diesem Satz zum ersten Mal begegnet, bereitet es häufig Schwierigkeiten, dass über die "Zwischenstelle" \(\xi\) nichts näheres bekannt ist.
Man kann damit auf verschiedene Arten umgehen: eine Möglichkeit besteht darin, alle möglichen Werte von \(f’(\xi )\) zu betrachten. Für \(f( x)=\sin ( x)\) und \([a,b] = [1,\displaystyle\frac {\pi }{2}]\) ist \(f’( x)=\cos ( x)\) und für \(\xi \in (1,\displaystyle\frac {\pi }{2} )\) liegt \(f’(\xi )\) damit im Intervall \(( 0,\cos (1))\). Man kann also aus dem Mittelwertsatz schließen, dass
\(\displaystyle\frac{\sin(1)-1}{1-\displaystyle\frac{\pi}{2}}\in(0,\cos(1)).\)
Man kann aber auch den "schlimmstmöglichen" Fall betrachten. Zum Beispiel ist für beliebige Zahlen \(x,y\in \mathbb {R}\)
\(\left|\displaystyle\frac{\cos( x)-\cos( y)}{x-y}\right|=|\sin(\xi)|\leq1\)
völlig unabhängig davon, was \(\xi \) genau ist. Damit erhält man die Ungleichung
\(|\cos( x)-\cos( y)|\leq|x-y|\)
die für alle \(x,y\in \mathbb{R}\) gültig ist.
Die Begründung ist eine elegante Anwendung des Mittelwertsatzes. Wir nehmen uns zwei beliebige Punkte \(a,b\in I\) und zeigen, dass \(f(a)=f(b)\) ist. Das folgt aber ganz direkt aus dem Mittelwertsatz, denn
\(f(a)-f(b)=\underbrace{f'(\xi)}_{=0}\cdot(a-b)=0\)
wobei man eben nicht wissen muss, wo genau \(\xi \) liegt, da die Ableitung überall verschwindet.
Sei \(f:\mathbb {R}\rightarrow \mathbb {R}\) eine differenzierbare Funktion, die die Differentialgleichung \(f’( x)=f( x)\) erfüllt und den Funktionswert \(f( 0)=1\) hat. Dann ist \(f( x)=e^ x\) für alle \(x\in \mathbb {R}\), denn:
Setze \(g( x):=f( x)e^{-x}\). Dann ist \( g’( x) =f’( x)e^{-x}-f( x)e^{-x}=0\). Also muss \(g\) konstant sein, d.h. \(g( x) \equiv \mathrm{const}=g( 0)=1\) für alle \(x\in \mathbb {R}\).
Daraus folgt wiederum \(f( x)e^{-x} = 1\) für alle \(x\) und daher \(f( x)= e^ x\).
-
\(f’( x)\geq 0\) für alle \(x\in I\Leftrightarrow f\) ist monoton wachsend, d.h. \(x<y\Rightarrow\,f( x)\leq f( y)\)
-
\(f’( x)>0\) für alle \(x\in I\Rightarrow f\) ist streng monoton wachsend, d.h. \(x<y\Rightarrow\,f( x)<f( y)\)
-
\(f’( x)\leq 0\) für alle \(x\in I\Leftrightarrow f\) ist monoton fallend, d.h. \(x< y\Rightarrow\,f( x)\geq f( y)\)
-
\(f’( x) <0\) für alle \(x\in I\Rightarrow f\) ist streng monoton fallend, d.h. \(x<y\Rightarrow f( y)<f( x)\)
Begründung: Wir zeigen nur die erste Behauptung (i), alle anderen kann man sich ganz analog überlegen. Die Äquivalenz "\(\Leftrightarrow \)" zerlegen wir dazu in zwei einzelne Behauptungen.
"\(\Rightarrow \)": Seien \(x,y\in I\) mit \(x \leq y\).
\(f’(\xi)=\displaystyle\frac{f( y)-f( x)}{y-x}\)
Da \(f’(\xi )\geq 0\) und \(y-x>0\), muss \(f( y)-f( x)\geq 0\) sein.
"\(\Leftarrow \)": Sei \(x_0\in I\) beliebig. Wähle eine Folge \((h_n)_{n\in \mathbb {N}}\) mit \(h_n>0\) und \(\lim \limits _{n\to \infty }h_n=0\). Dann ist \(f( x_0+h_ n)-f( x_0)\geq 0\). Da \(f\) in \(x_0\) differenzierbar ist, existiert der Grenzwert
\(f’(x)=\lim\limits_{n\to\infty}\underbrace{\displaystyle\frac{f( x_0+h_n)-f( x_0)}{h}}_{\geq 0}\geq 0\)
falls \(x_0\) nicht der rechte Randpunkt ist.
□
-
Die Exponentialfunktion \(f( x)=e^x\) hat die Ableitung \(f’( x)=e^ x>0\) und ist daher streng monoton wachsend. (Ok, das wussten wir schon, aber zumindest kommt auf diese Weise nicht das Gegenteil heraus.)
-
Die Funktion \(h( x)=\displaystyle\frac {1}{1+x^2}\) hat die Ableitung \(h’( x)=\displaystyle\frac {-2x}{(1+x^2)^2}\). Daher ist \(h’( x)<0\) auf \(( 0,\infty )\), d.h. die Funktion ist dort streng monoton fallend.
-
Die Sinusfunktion \(f( x)=\sin x\) hat die Ableitung \(f’( x)=\cos x\), die auf dem Intervall \((-\displaystyle\frac {\pi }{2},\displaystyle\frac {\pi }{2})\) positiv ist und ist daher auf diesem Intervall streng monoton wachsend.
