13.2 Extrema
13.2 Lokale Extrema
Eine der wichtigsten Anwendungen der Ableitung ist die Bestimmung von Maxima und Minima einer Funktion.
Genauer gesagt kann man mit Hilfe der Ableitung nach sogenannten lokalen Maxima suchen. Das sind Punkte, deren Funktionswert größer ist als alle Funktionswerte in der Nähe. Mathematisch präzise lässt sich das so definieren:
Sei \(I\subset \mathbb {R}\) ein Intervall und \(f:I\rightarrow \mathbb {R}\) eine stetige Funktion.
Ein Punkt \(x_0\in I\) heißt lokales Maximum von \(f\), wenn es eine Zahl \(\delta >0\) gibt, so dass für alle \(x\in I\) gilt:
\(\left| x-x_0 \right| < \delta \Rightarrow f(x)\leq f(x_0)\)
Analog heißt ein Punkt \(x_0\in I\) lokales Minimum von \(f\), wenn es eine Zahl \(\delta >0\) gibt, so dass für alle \(x\in I\) gilt:
\(\left|x-x_0\right|< \delta \Rightarrow f(x)\geq f(x_0)\)
Ein Punkt \(x_0\in I\) heißt lokales Extremum von \(f\), wenn \(x_0\) entweder ein lokales Maximum oder ein lokales Minimum ist.
Ein Punkt \(x_0\in I\) heißt globales Maximum von \(f\), wenn \(f(x_0)\geq f(x)\) für alle \(x\in I\) ist und globales Minimum von \(f\), wenn \(f(x_0)\leq f(x)\) für alle \(x\in I\) ist.
Mit Hilfe der Ableitung kann man feststellen, an welcher Stelle ein lokales Maximum oder Minimum liegen könnte.
Beweis des Satzes: Wir nehmen an, dass \(f\) bei \(x_0\) ein lokales Minimum hat. Am Ende wird noch gezeigt, wie man die Argumentation modifizieren muss, wenn \(x_0\) kein lokales Minimum, sondern ein lokales Maximum von \(f\) ist.
Zunächst wählen wir eine kleine Zahl \(\delta >0\) so, dass \(f(x)\geq f(x_0)\) für alle \(x\) im Intervall \((x_0-\delta ,x_0+\delta )\), also genau wie in der Definition des lokalen Minimums. Wenn wir nun \(n\) sehr groß wählen, also \(\displaystyle\frac {1}{n}\) sehr klein, dann liegt \(x_0-\displaystyle\frac {1}{n}\) und \(x_0+\displaystyle\frac {1}{n}\) in diesem Intervall \((x_0-\delta ,x_0+\delta )\). Nun berechnen wir die Ableitung der Funktion \(f\) in \(x_0\) auf zwei Arten. Einerseits ist
\(f’(x_0)=\lim\limits_{n\to\infty}\displaystyle\frac{f( x_0+\displaystyle\frac{1}{n})-f( x_0)}{\displaystyle\frac{1}{n}}\geq 0,\)
da sowohl Zähler als auch Nenner des Bruches nicht-negativ sind. Andererseits ist
\(f’(x_0)=\lim\limits_{n\to\infty}\displaystyle\frac{f(x_0-\displaystyle\frac{1}{n})-f(x_0)}{-\displaystyle\frac{1}{n}}\leq 0,\)
da hier der Zähler nicht-negativ, der Nenner aber immer negativ ist. Beide Ungleichungen zusammen können nur erfüllt sein, wenn \(f’(x_0)=0\) ist.
Wenn \(x_0\) kein lokales Minimum, sondern ein lokales Maximum von \(f\) ist, dann betrachtet man statt \(f\) die (an der x-Achse gespiegelte) Funktion \(g(x)=-f(x)\), die dann in \(x_0\) ein lokales Minimum hat. Wie gerade eben gezeigt, ist dann \(g’(x_0)=0\), also auch \(f’(x_0)=-g’(x_0)=0\).
?
\(f(x)=\sum\limits_{j=1}^n(x-x_j)^2\)
bestimmen. Hier werden einerseits Abweichungen in beide Richtungen immer mit positivem Vorzeichen gezählt, andererseits gehen größere Abweichungen mit stärkerem Gewicht in die Summe ein. Die Ableitung ist\(f’(x)=2\sum\limits_{j=1}^n(x-x_j)\)
und verschwindet genau für\(\bar{x}=\displaystyle\frac{x_1+x_2+\dots+x_n}{n}\)
also für den Mittelwert (genauer: das arithmetische Mittel ) der Messwerte. Man kann sich überlegen, dass für \(x\to \pm \infty \) immer \(f\left(x\right)\to +\infty \) gilt, da die Messwerte \(x_1,\dots , x_ n\) ja feste Zahlen sind, und da es nur einen Kandidaten für ein Extremum gibt, muss in \(\bar{x}\) ein Minimum vorliegen.\(x_0\in I\) heißt kritischer Punkt von \(f\), wenn \(f’(x_0)=0\).
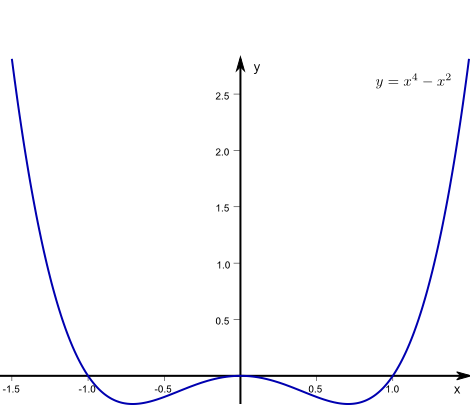
- Wir betrachten die Funktion \(f( x)=x^4-x^2\) von oben.
Ihre Ableitung ist \(f’( x)=4x^3-2x\) und die Bedingung \(f’(x)=0\Leftrightarrow 2x( 2x^2-1)\) führt auf die drei kritischen Punkte\(x_1=0,\;\;x_{2,3}=\pm\displaystyle\frac{1}{\sqrt{2}},\)
die wir ja bereits aus unserer Skizze kennen. - \(f( x)=x^3\)
Hier ist \(f’(0)=0\), d.h. \(x_0=0\) ist ein kritischer Punkt. Dort ist aber kein lokales Extremum, die Bedingung \(f’(x_0)=0\) ist nur notwendig , aber nicht hinreichend !
Um bei einem kritischen Punkt zu entscheiden, ob es sich um ein lokales Maximum, Minimum oder keines von beiden handelt, benötigen wir noch weitere Informationen. Dabei erweist sich die zweite Ableitung als nützlich.
Sei \(f\colon(a,b)\to \mathbb {R}\) zweimal differenzierbar und \(f''\) eine stetige Funktion. Falls für ein \(x_0\in (a,b)\)
\(f'(x_0)=0\) und \(f''(x_0)<0,\)
dann hat \(f\) in \(x_0\) ein striktes lokales Maximum, d.h. es gibt ein \(\varepsilon >0\), so dass gilt:
\(|x-x_0|\leq\varepsilon\;\;\Rightarrow\,f(x)< f(x_0).\)
Analog hat \(f\) ein striktes lokales Minimum in \(x_0\), falls \(f'( x_0)=0\) und \(f''( x_0)>0\).
Beweis: Wir betrachten nur den Fall eines Maximums. Da \(f''(x_0)<0\) gibt es eine Umgebung \((x_0-\varepsilon ,x_0+\varepsilon )\) in der \(f''\) negativ ist. Also ist \(f'\) in dieser Umgebung streng monoton fallend. Da \(f'( x_0)=0\) ist also \(f'( x)>0\) für \(x\in (x_0-\varepsilon ,x_0)\) und \(f'( x)<0\) für \(x\in (x_0,x_0+\varepsilon )\). Also ist \(f\) links von \(x_0\) streng monoton wachsend und rechts von \(x_0\) streng monoton fallend.
Aus einem rechteckigen Blech der Seitenlängen \(a\leq b\) soll ein Kasten von möglichst großem Volumen \(V\) in den RUB-Farben hergestellt werden.
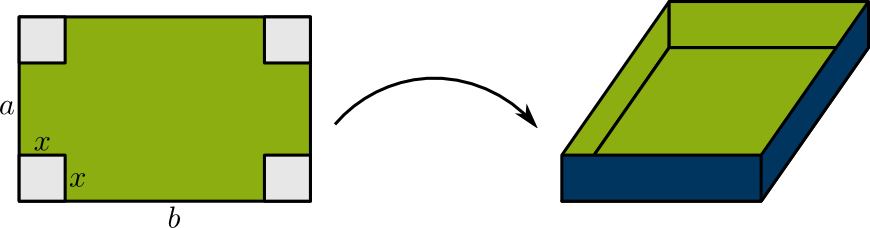
Wie muss die Länge \(x\) gewählt werden, damit \(V\) maximal wird?
Das Volumen lässt sich als Funktion von \(x\) berechnen als
\(V( x)=(a-2x)(b-2x) x = ab x - 2 ( a+b ) x^2+ 4x^3 \)
mit der Ableitung
\(V’(x)=ab-4(a+b)x+12x^2\)
Die kritischen Punkte sind also bei
\(x_{1,2}=\displaystyle\frac{4(a+b)\pm\sqrt{16(a+b)^2-48ab}}{24}=\displaystyle\frac{(a+b)\pm\sqrt{a^2+b^2-ab}}{6}\)
Dass das Volumen
\(x_1=\displaystyle\frac{(a+b)-\sqrt{a^2+b^2-ab}}{6}\)
ein Maximum annimmt, kann man auf zwei Arten nachprüfen. Zum einen kann man den Verlauf einer kubischen Parabel skizzieren und daraus schließen, dass von den beiden kritischen Punkten der kleinere ein Maximum und der größere ein Minimum sein muss, man könnte aber auch die zweite Ableitung berechnen und nachprüfen, dass \(V”(x_1)<0\) ist.
