11.2 Umkehrfunktionen und Wurzeln

Sei \(f\colon [a,b]\to \mathbb {R}\) eine Funktion, die auf dem Intervall \([a,b]\) definiert ist.

Dann wird jedem \(x\in [a,b]\) ein eindeutiges \(y=f( x)\) zugeordnet. Oft möchte man aber zu dem Funktionswert \(y\) das entsprechende \(x\) finden. Dabei hilft die Umkehrfunktion oder inverse Funktion von \(f\).

Definition (Invertierbarkeit):
Sei \(f\! :\! D\to \mathbb {R}\) eine Funktion mit Definitionsbereich \(D\) und Wertebereich \(W=f(D)\).
Dann heißt \(f\) invertierbar (oder umkehrbar), falls jedem \(y\in W\) genau ein \(x\in D\) entspricht mit \(f(x)=y\). Die Abbildung \(f^{-1}:W\to ~ D\), die jedem \(y\in W\) dieses \(x\) zuordnet heißt Umkehrfunktion oder inverse Funktion von \(f\).

Bemerkung:
Die Bezeichnung \(f^{-1}\) steht meistens für die Umkehrfunktion von \(f\), manchmal aber auch für das Urbild einer Menge unter der Funktion \(f\). Was gemeint ist, muss man sich aus dem Zusammenhang klarmachen.

Beispiel (Umkehrfunktion einer linearen Funktion):
Bei einer linearen Funktion \(f(x)=mx+b\) kann man die Umkehrfunktion durch "Auflösen nach \(x\)" direkt berechnen:

\(x=\displaystyle \frac{y-b}{m}=\frac{1}{m}y-\frac{b}{m}=f^{-1}( y)\)

In diesem Fall ist \(f^{-1}\) nun eine von der Variablen \(y\) abhängige Funktion. Allerdings ist es in der Mathematik oft üblich, die unabhängige Variable mit \(x\) zu bezeichnen und so werden an dieser Stelle meist die Variablen getauscht bzw.< umbenannt und man schreibt

\(f^{-1}(x)=\frac{1}{m}x-\frac{b}{m}.\)

Insbesondere ist die Umkehrfunktion einer linearen Funktion wieder eine lineare Funktion.

Dies ist auch geometrisch sehr schön einzusehen, wenn man berücksichtigt, dass das Schaubild der Umkehrfunktion \(f^{-1}\) aus dem Schaubild von \(f\) durch Spiegelung an der Diagonalen hervorgeht.

Figures/umkehrfunktion_spiegelung

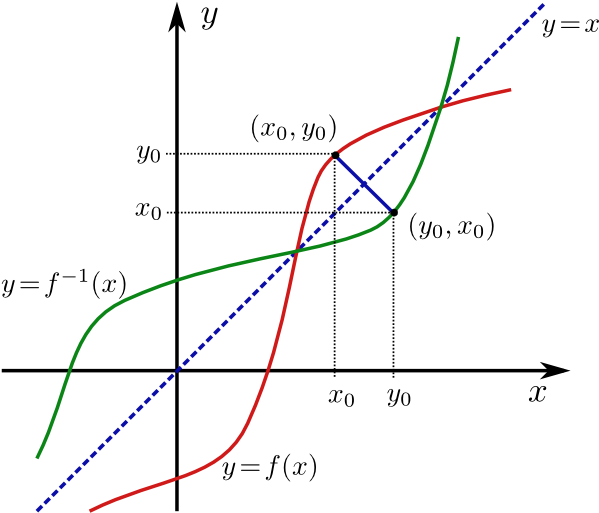
Zur Begründung betrachten wir irgendein \(x_0\) und setzen \(y_0=f(x_0)\). Dann liegt der Punkt \((x_0,y_0)\) auf dem Schaubild von \(f\). Dieser Punkt geht durch Spiegelung an der Winkelhalbierenden \(x=y\) in den Punkt \((y_0,x_0)\) über. Andererseits ist \(x_0=f^{-1}(y_0)\), falls \(f\) eine invertierbare Funktion ist, d.h. \(x_0\) ist der Funktionswert von \(f^{-1}\) an der Stelle \(y_0\) und \((y_0,x_0)\) liegt damit auf dem Schaubild von \(f^{-1}\).

n-te Wurzeln

Zu einer natürlichen Zahl \(n\in \mathbb{N}\) betrachten wir die Potenzfunktion \(f(x)=x^ n\). Diese ist nicht unbedingt eine monotone Funktion, daher unterscheiden wir zwei Fälle:

1.Fall: \(n\) ist ungerade
In diesem Fall ist \(f\) auf ganz \(\mathbb{R}\) eine streng monoton wachsende Funktion und es gilt \(\lim \limits_{x\to -\infty }f(x)=-\infty \) und \(\lim \limits _{x\to +\infty }f(x)=+\infty \), der Wertebereich von \(f\) ist also ganz \(\mathbb{R}\). Daher besitzt \(f\) eine auf ganz \(\mathbb {R}\) definierte Umkehrfunktion \(f^{-1}\).
2.Fall: \(n\) ist gerade
In diesem Fall ist \(f(-x)=f(x)\) und \(f\) ist nur auf \((-\infty ,0]\) bzw. auf \([0,\infty )\) streng monoton. Wenn wir \(f\) nur noch mit dem Definitionsbereich \([0,\infty )\) betrachten, ist der Wertebereich ebenfalls \([0,\infty )\) und es gibt zu jedem \(y\geq 0\) genau ein \(x\in [0,\infty )\) mit \(x^ n=y\). Dieses \(x\) ist die n-te Wurzel von \(y\), geschrieben \(x=\sqrt [n]{y}\). Die Umkehrfunktion von \(f\) ist also \(f^{-1}:[0,\infty )\to [0,\infty )\) mit \(f^{-1}(x)=\sqrt [n]{x}\).

Bemerkung:
Es kann durchaus vorkommen, dass eine Funktion zwar umkehrbar ist, man die Umkehrfunktion aber nicht durch Wurzeln oder andere bekannte Funktionen ausdrücken kann. Zum Beispiel ist die Funktion \(f(x)=x^5+x+1\) sicher auf ganz \(\mathbb{R}\) monoton wachsend und damit invertierbar, aber die Gleichung \(x^5+x+1=y\) lässt sich nicht explizit nach \(x\) auflösen. Es gibt also eine Umkehrfunktion, wir können sie aber nicht einfach hinschreiben. Das mag einem zwar unsympathisch sein, dennoch ist es hin und wieder nötig, auch mit solchen Funktionen zu rechnen.

Zuletzt geändert: Sonntag, 20. Januar 2019, 13:13