11.1 Polynome
Kapitel 11: Elementare Funktionen
11.1 Polynome
Viele physikalische Zusammenhänge lassen sich durch Gesetzmäßigkeiten der Form \(y=c\cdot x^n\) mit \(n\in \mathbb{N}\) beschreiben. Zugegeben, meist ist sogar \(n=1\) oder \(2\), aber hin und wieder kommen auch ein paar größere Zahlen vor. Zum Beispiel beträgt das Flächenträgheitsmoment eines Balkens der Breite b und Höhe h mit rechteckigem Querschnitt \(\displaystyle\frac {1}{12}bh^3\).
Wenn mehrere Einflüsse eine Rolle spielen, dann addieren sich diese oft. Solche Zusammenhänge werden dann durch Polynome beschrieben.
$p(x) = a_0 + a_1x+a_2x^2+\ldots+a_nx^n$
heißt Polynom oder ganzrationale Funktion. Die Zahlen $a_0,a_1,\ldots,a_n$ heißen Koeffizienten, die größte Zahl n, für die \(a_n\neq 0\) ist, nennt man den Grad des Polynoms.
Mit Hilfe des Summenzeichens kann man ein Polynom auch sehr kompakt als
\(p(x)=\sum\limits_{k=0}^na_kx^k\)
schreiben.
Am häufigsten begegnet man den rationalen Funktionen mit kleinem Grad also
-
den affin-linearen Funktionen p(x) = a0 + a1 x vom Grad 1,
-
den quadratischen Funktionen p(x) = a0 + a1 x + a2 x2 vom Grad 2 und
-
den kubischen Funktionen \(p(x)=a_0+a_1 x+a_2 x^2 + a_3 x^3\) vom Grad \(3\).
Affin-lineare Funktionen hatten wir im Abschnitt über Geraden schon behandelt. Sie sind sehr häufig, aber auch quadratische Funktionen findet man nicht so selten, da man deren Nullstellen explizit berechnen kann.
Allgemeine Potenzfunktionen
Für \(n\in \mathbb{N}\) ist die n-te Potenz $x^n$ einer Zahl n eine Kurzschreibweise für das n-malige Produkt der Zahl mit sich selbst:
$x^n = \underbrace{x\cdot x \cdot x \cdot \dots \cdot x}_{n\; \; \text { Faktoren}}$
Für diese gilt \(x^n \cdot x^m = x^{n+m}\), wie man sich durch Abzählen der Faktoren klarmacht.
Setzt man \(x^0 := 1\) und \(x^{-n} :=\displaystyle\frac {1}{x^n}\), so gilt diese Regel weiter, und zwar für \(m,n\in \mathbb{Z}\).
-
\(x^n \cdot x^m = x^{n+m}\)
-
\(\displaystyle\frac {x^n}{x^ m} = x^{n-m}\)
-
\(\left(x^ n\right)^ m = x^{n\cdot m}\)
Potenzgesetze benutzt man, wenn es darum geht, die Dimension von physikalischen Größen zu bestimmen.
Das Newtonsche Gravitationsgesetz sagt aus, dass zwei Körper der Massen \(m\) und \(M\), die den Abstand \(r\) voneinander haben sich mit der Kraft
\(F=\gamma\displaystyle\frac{mM}{r^2}\)
gegenseitig anziehen. Um die Dimension der Gravitationskonstante \(\gamma \) zu bestimmen, betrachtet man die Einheiten
\(\left[\displaystyle\frac{kg\, m}{s^2}\right]=\left[\gamma\right]\cdot\left[\displaystyle\frac{kg^2}{m^2}\right]\)
woraus als Einheit von \(\gamma \) folgt
$\left[\gamma\right]=\displaystyle\frac{\left[\displaystyle\frac{kg \cdot m}{s^2}\right]}{\left[\displaystyle\frac{kg^2}{m^2}\right]} =\left[\displaystyle\frac{kg^{1-2}\cdot m^{1+2}}{s^2}\right]=\left[\displaystyle\frac{m^3}{kg\cdot s^2}\right]$
Diese Potenzgesetze bleiben weiter gültig, wenn man
\(x^{\frac{m}{n}}:=\sqrt[n]{x^m}\)
setzt, also insbesondere \(x^{1/n}=\sqrt[n]{x}\). Das funktioniert dann nur noch für \(x\geq 0\), da man aus negativen Zahlen keine Wurzeln ziehen kann.
Später werden wir \(x^{\alpha}\) auch für irrationale \(\alpha \) betrachten, aber dazu muss man Grenzwerte betrachten, im Moment beschränken wir uns daher auf rationale \(\alpha \).
Das folgende Diagramm zeigt die Schaubilder von Potenzfunktionen \(x^{m/n}\) für verschiedene Exponenten:
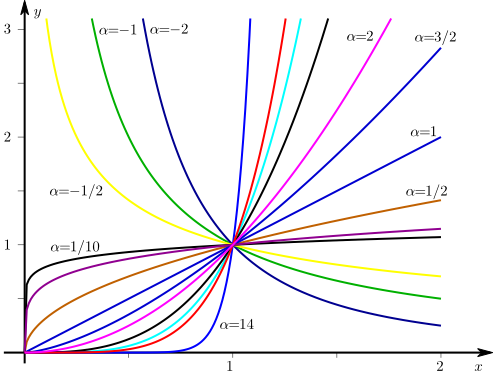
-
alle Schaubilder sind monoton: wachsend für \(\alpha >0\) und fallend für \(\alpha <0\)
-
alle Schaubilder verlaufen durch den Punkt \((1,1)\)
-
Für $\alpha >0$ verlaufen die Schaubilder durch den Punkt \((0,0)\)
-
Für \(\alpha <0\) konvergieren die Funktionswerte für \(x\to 0\) gegen \(+\infty \) und für \(x\to \infty \) gegen \(0\)
Rationale Funktionen
\(f(x)=\displaystyle\frac{p(x)}{q(x)}\)
wobei \(p\) und \(q\) Polynome sind.
Der Definitionsbereich von \(f\) ist \(\mathbb {R}{\setminus }N_ q\), wobei \(N_ q\) die Nullstellenmenge von \(q\) ist. Eine rationale Funktion ist auf ihrem ganzen Definitionsbereich stetig. Was das Verhalten in der Nähe der Definitionslücken angeht, so handelt es sich typischerweise um Polstellen.
Sei \(x_0\in N_ q\) eine Nullstelle von \(q\). Wir bezeichnen mit \(r>0\) die Vielfachheit der Nullstelle \(x_0\) als Nullstelle von \(q\) und mit \(s\geq 0\) die Vielfachheit von \(x_0\) als Nullstelle von \(p\), wobei \(s=0\), falls \(p(x_0)\neq 0\) ist. Dann gilt:
-
im Fall \(r > s\) hat \(f\) in \(x_0\) eine Polstelle der Ordnung \((r-s)\). Das heißt, wenn man Terme \((x-x_0)\) soweit möglich kürzt, hat \(f\) die Form
\(f(x)=\displaystyle\frac{\tilde{p}(x)}{(x-x_0)^{r-s}\tilde{q}(x)}\)
wobei \(\tilde{p}(x_0),\tilde{q}(x_0)\neq 0\) sind.
Eine ungerade Ordnung bedeutet dabei, dass \(f\) auf beiden Seiten der Polstelle verschiedene Vorzeichen hat, bei einer geraden Ordnung stimmen die Vorzeichen überein. -
im Fall \(r\,\leq\, s\) ist \(x_0\) eine hebbare Unstetigkeitsstelle, das heißt, man könnte im Zähler und Nenner den Term \((x-x_0)^r\) kürzen und würde auf diese Weise eine in \(x_0\) stetige Funktion erhalten. Die Definitionslücke bei \(x_0\) ist also künstlich (oder noch deutlicher gesagt, "eigentlich unnötig"). Wenn \(f\) sich stetig nach \(x_0\) fortsetzen lässt, dann kann das Problem, das \(f\) an der Stelle \(x_0\) hat, "behoben" werden, indem man \(f( x_0)\) geeignet definiert.
