4.1 Lineare Gleichungssysteme
Kapitel 4: Lineare Gleichungssysteme
4.1 Lineare Gleichungssysteme
Eine große Klasse von Gleichungen, die man im Prinzip explizit lösen kann, sind die linearen Gleichungen in \(n\) Variablen.
Ein lineares Gleichungssystem (LGS) mit \(m\) Gleichungen und \(n\) Unbekannten \(x_1,x_2,\ldots , x_ n\) ist ein System von Gleichungen der Form
\( \begin{align*} a_{11}x_1+a_{12}x_2+\ldots+a_{1n}x_n&=b_1\\a_{21}x_1+a_{22}x_2+\ldots+a_{2n}x_n&=b_2\\\vdots\hspace{5em}&\vdots\\a_{m1}x_1+a_{m2}x_2+\ldots+a_{mn}x_n&=b_m \end{align*} \)
Es dürfen also keine "nichtlinearen" Terme wie \(x_1\cdot x_2\) oder \(\sin (x_1)\) oder \(x_3^2\) auftauchen.
Harnstoff reagiert mit salpetriger Säure zu Kohlendioxid, Stickstoff und Wasser. In der zugehörigen Reaktionsgleichung
\(CH_4N_2O+a\,HNO_2\rightarrow\,b\,CO_2+c\,N_2+d\,H_2O\)
sollen natürliche Zahlen \(a\), \(b\), \(c\) und \(d\) bestimmt werden, so dass für jedes Element die Anzahl der Atome in den Ausgangsstoffen und in den Endstoffen übereinstimmt.
\( \begin{align*} \text{Kohlenstoff:}&&1&=b\\\text{Wasserstoff:}&&4+a&=2d\\\text{Stickstoff:}&&2+a&=2c\\\text{Sauerstoff:}&&1+2a&=2b+d \end{align*} \)
Setzt man \(b=1\) in die letzte Gleichung ein und multipliziert mit zwei, so erhält man \(4a-2 = 2d\) und durch Vergleich mit der zweiten Gleichung folgt \(4+a=4a-2\) also \(a=2\), woraus sich für die übrigen Unbekannten \(d=3\) und \(c=2\) ergibt.
2\(\cdot \)(Anzahl der Knoten) -3 = Anzahl der Verbindungen
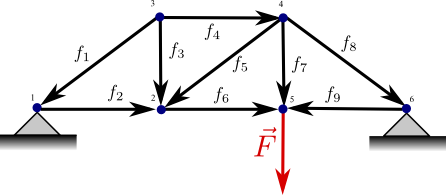
Man erkennt, dass schon bei relativ "einfachen" mechanischen Systemen, die zugehörigen linearen Gleichungssysteme etwas unübersichtlich werden können. Die Multiplikation von Matrizen und Vektoren kann man verwenden, um lineare Gleichungssysteme in kompakter Form aufzuschreiben und zu lösen.
Bei der Lösung des ersten Beispiels sind wir ziemlich ungeordnet ("ad hoc") vorgegangen. Ziel dieses Abschnitts ist es auch, ein systematisches Verfahren zu erlernen, mit dem man im Prinzip beliebig große lineare Gleichungssysteme lösen kann.
Definiert man die Koeffizientenmatrix \(A=(a_{ij})\) durch die Koeffizienten des Gleichungssystems, den Spaltenvektor \(x\in \mathbb {R}^ n\) durch die unbekannten Variablen \(x_1,x_2,\ldots ,x_ n\) und den Spaltenvektor \(b\in \mathbb {R}^ m\) durch die rechte Seite des Gleichungssystems, dann kann man es in der Form
\(Ax=b\Leftrightarrow\left(\begin{array}{cccc}a_{11}&a_{12}&\ldots&a_{1n}\\a_{21}&a_{22}&\ldots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{m1}&a_{m2}&\ldots&a_{mn}\end{array}\right)\left(\begin{array}{r}x_1\\x_2\\\vdots\\x_n\end{array}\right)=\left(\begin{array}{r}b_1\\b_2\\\vdots\\b_m\end{array}\right)\)
schreiben.
Wenn \(b=0\) der Nullvektor ist, dann nennt man das Gleichungssystem homogen . In diesem Fall ist der Vektor \(x=0\) immer eine Lösung des Gleichungssystems.
Falls \(b\neq 0\) nicht der Nullvektor ist, dann gibt es mehrere Möglichkeiten.
-
das Gleichungssystem hat keine Lösung. Dies ist meist (aber nicht immer) der Fall, wenn die Anzahl der Gleichungen größer ist als die Zahl der Unbekannten (m>n).
-
das Gleichungssystem hat genau eine Lösung. Dies ist meist (aber nicht immer) der Fall, wenn die Anzahl der Gleichungen gleich der Zahl der Unbekannten ist (m=n).
-
das Gleichungssystem hat unendlich viele Lösungen. Dies ist meist (aber nicht immer) der Fall, wenn die Anzahl der Gleichungen kleiner ist als die Zahl der Unbekannten (m<n).
Im Gegensatz zu quadratischen Gleichungen ("p-q-Formel") kann es bei linearen Gleichungssystemen beispielsweise nie passieren, dass genau zwei Lösungen existieren. Wir werden als nächstes genau beschreiben, wie man herausfindet, wie viele und welche Lösungen ein lineares Gleichungssystem hat.
