2.3 Das Kreuzprodukt
Für Vektoren im Raum gibt es eine weitere Verknüpfungsmöglichkeit, das Kreuzprodukt. Es hat die Eigenschaften, dass zwei Vektoren \(\vec{a}\) und \(\vec{b}\) ein dritter Vektor \(\vec{a}\times \vec{b}\) zugeordnet wird, der senkrecht auf derjenigen Ebene steht, die \(\vec{a}\) und \(\vec{b}\) enthält.
\(\vec{a}\times\vec{b}=\left(\begin{array}{r}a_1\\a_2\\a_3\end{array}\right)\times\left(\begin{array}{r}b_1\\b_2\\b_3\end{array}\right)=\left(\begin{array}{r}a_2b_3-a_3b_2\\a_3b_1-a_1b_3\\a_1b_2-a_2b_1\end{array}\right)\)
Kreuzprodukt oder Vektorprodukt von \(\vec{a}\) und \(\vec{b}\).
Die Rechenvorschrift kann man sich etwas leichter anhand des Schemas

merken, bei dem man die beiden ersten Komponenten der Vektoren noch einmal hinschreibt, und dann die Komponenten des Kreuzprodukts als "‘Produkte über Kreuz"’ berechnet.
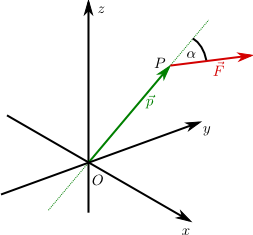
Ein weiteres Beispiel aus der Physik, bei dem das Kreuzprodukt auftritt, ist die Lorentz-Kraft \(\vec{F} = q(\vec{v} \times \vec{B})\), die von einem Magnetfeld der Induktion \(\vec{B}\) auf eine Ladung \(q\) ausgeübt wird, wenn diese sich mit der Geschwindigkeit \(\vec{v}\) im Magnetfeld bewegt.
Sind \(\vec{a}\) und \(\vec{b}\) zwei Vektoren im \(\mathbb {R}^3\), dann ist
\(|\vec{a}\times\vec{b}|=|\vec{a}|\cdot|\vec{b}|\cdot\sin\alpha\)
wobei \(\alpha\) der Winkel zwischen den Vektoren \(\vec{a}\) und \(\vec{b}\) ist.
Außerdem ist \(|\vec{a}\times \vec{b}|\) der Flächeninhalt des von \(\vec{a}\) und \(\vec{b}\) aufgespannten Parallelogramms.

Beweis: Wir berechnen
\( \begin{align*} |\vec{a}\times\vec{b}|^2&=(\vec{a}\times\vec{b})\cdot(\vec{a}\times\vec{b})\\&=(a_2b_3-a_3b_2)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2\\&=(a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^2)-(a_1b_1+a_2b_2+a_3b_3)^2\\&=|\vec{a}|^2\cdot|\vec{b}|^2-\left(\vec{a}\cdot\vec{b}\right)^2\\&=|\vec{a}|^2\cdot|\vec{b}|^2-\left(|\vec{a}|\cdot|\vec{b}|\cos(\alpha)\right)^2\\&=|\vec{a}|^2\cdot|\vec{b}|^2\cdot\underbrace{(1-\cos^2(\alpha))}_{=\sin^2(\alpha)}\\&=\left(|\vec{a}|\cdot|\vec{b}|\cdot\sin(\alpha)\right)^2 \end{align*} \)
Da \(\alpha \) zwischen \(0\) und \(\pi\) liegt, ist \(\sin (\alpha)\) positiv und wenn man die Wurzel auf beiden Seiten der Ungleichung zieht, erhält man
\(|\vec{a}\times\vec{b}|=|\vec{a}|\cdot|\vec{b}|\cdot\sin(\alpha)\)
Der Flächeninhalt des Parallelogramms ist "‘Grundseite mal Höhe"’, also ebenfalls
\(|\vec{a}|\cdot h=|\vec{a}|\cdot(|\vec{b}|\,\sin(\alpha))\)
?
Die folgenden Rechenregeln ergeben sich zwar ohne großen Aufwand aus der Definition des Kreuzprodukts, man sollte sie sich aber gut einprägen, da sie teilweise anders sind, als man dies vom "‘normalen"’ produkt zweier Zahlen gewohnt ist.
-
\(\vec{a}\times \vec{a} = \vec{0}\) für jeden Vektor \(\vec{a}\)
-
\(\vec{a}\times \vec{b} = -\vec{b}\times \vec{a}\)
-
\(\vec{a}\times (\vec{b} \times \vec{c}) = (\vec{a}\cdot \vec{c})\vec{b}- (\vec{a}\cdot \vec{b})\vec{c}\)
-
\((\vec{a}\times \vec{b})\cdot (\vec{c} \times \vec{d}) = (\vec{a}\cdot \vec{c})(\vec{b}\cdot \vec{d})- (\vec{a}\cdot \vec{d})(\vec{b}\cdot \vec{c})\)
Insbesondere ist
\((\vec{a}\times\vec{b})\times\vec{c}=-\vec{c}\times(\vec{a}\times\vec{b})=-(\vec{c}\cdot\vec{b})\vec{a}+(\vec{c}\cdot\vec{a})\vec{b}\neq\vec{a}\times(\vec{b}\times\vec{c})\)
Das Spatprodukt
\([\vec{a},\vec{b},\vec{c}]=\vec{a}\cdot(\vec{b}\times\vec{c})\)
Geometrisch gibt \(|[\vec{a},\vec{b},\vec{c}]|\) das Volumen des Spats (oder Parallelepipeds, Parallelotop) an, das von den drei Vektoren \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) aufgespannt wird:
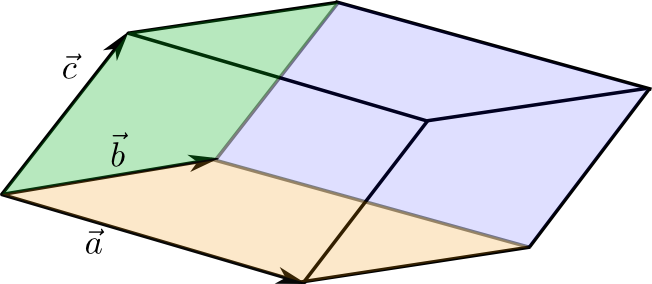
Dabei handelt es sich um die räumliche Variante eines Parallelogramms, d.h. die sechs Seitenflächen sind drei Paare von kongruenten, parallelen Parallelogrammen. Für das Spatprodukt gelten die folgenden Rechenregeln:
- Wenn einer der Vektoren mit der Zahl \(\lambda\) multipliziert wird, dann wird auch das Spatprodukt mit \(\lambda\) multipliziert:
\([\lambda\vec{a},\vec{b},\vec{c}]=[\vec{a},\lambda\vec{b},\vec{c}]=[\vec{a},\vec{b},\lambda\vec{c}]=\lambda\cdot[\vec{a},\vec{b},\vec{c}]\)
- Das Spatprodukt bleibt unverändert, wenn man zu einem der Vektoren einen der beiden anderen addiert:
\([\vec{a},\vec{b}+\vec{a},\vec{c}]=[\vec{a},\vec{b},\vec{c}+\vec{a}]=[\vec{a}+\vec{b},\vec{b},\vec{c}]=\dots=[\vec{a},\vec{b},\vec{c}]\)
- Für die Standardeinheitsvektoren gilt
\([\vec{e}_1,\vec{e}_2,\vec{e}_3]=1.\)
Beweis durch Nachrechnen:
-
nur für die ersten beiden Varianten:
\([\lambda\vec{a},\vec{b},\vec{c}]=\lambda\vec{a}\cdot(\vec{b}\times\vec{c})=\lambda[\vec{a},\vec{b},\vec{c}]\)
\([\vec{a},\lambda\vec{b},\vec{c}]=\vec{a}\cdot(\lambda\vec{b}\times\vec{c})=\vec{a}\cdot\lambda(\vec{b}\times\vec{c})=\lambda\cdot[\vec{a},\vec{b},\vec{c}]\)
-
auch hier nur exemplarisch ein Fall:
\([\vec{a},\vec{b}+\vec{a},\vec{c}]=\vec{a}\cdot((\vec{b}+\vec{a})\times\vec{c})=\vec{a}\cdot(\vec{b}\times\vec{c}+\vec{a}\times\vec{c})=\vec{a}\cdot(\vec{b}\times\vec{c})+\underbrace{\vec{a}\cdot(\vec{a}\times\vec{c})}_{=0}=[\vec{a},\vec{b},\vec{c}]\)
da der Vektor \(\vec{a}\times \vec{c}\) senkrecht zu \(\vec{a}\) ist.
-
Direkt nachrechnen:
\([\vec{e}_1,\vec{e}_2,\vec{e}_3]=\vec{e}_1\cdot(\underbrace{\vec{e}_2\times \vec{e}_3}_{=\vec{e}_1})= 1\)
□
- Es ist \([\vec{a},\vec{b},\vec{c}] = 0\) genau dann, wenn die drei Vektoren \(\vec{a},\vec{b}\) und \(\vec{c}\) in einer Ebene liegen. Man kann also mit Hilfe des Spatprodukts überprüfen, ob drei Vektoren im \(\mathbb{R}^3\) linear unabhängig sind oder nicht.
- Das Spatprodukt lässt sich auch mit Hilfe von Determinanten (siehe Kapitel 6) berechnen:
\([\vec{a},\vec{b},\vec{c}]=\det\left(\begin{array}{ccc}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{array}\right)\)
