2.1 Vektoren
Kapitel 2: Vektoren
2.1 Vektoren
Kartesische Koordinaten
Wir wollen in diesem Kapitel ein wenig Analytische Geometrie betreiben, d.h. geometrische Objekte durch Zahlen und Gleichungen beschreiben.
Dazu benötigen wir als erstes einen besonderen Punkt 0, den wir Ursprung nennen und von dem aus wir unsere Messungen durchführen. Darüber hinaus brauchen wir noch zwei zueinander senkrechte durch 0 verlaufende Geraden angibt, die x- und y-Achse, und auf diesen eine Maßeinheit zum Messen von Entfernungen. Man nennt dies ein Kartesisches Koordinatensystem der Ebene \(\mathbb {R}^2=\mathbb {R}\times \mathbb {R}\). Typischerweise ist dies alles schon gegeben, wenn wir anfangen zu rechnen, aber wir werden uns später Gedanken machen, was zu tun ist, wenn man von einem gegebenen kartesischen Koordinatensystem in ein anderes (zum Beispiel gedrehtes) Koordinatensystem wechseln will.
Üblicherweise werden die Bezeichnungen so gewählt, dass man die x-Achse durch eine Drehung um \(90^{\circ }\) gegen den Uhrzeigersinn in die y-Achse überführen kann. Durch die Koordinatenachsen wird die Ebene in vier Quadranten Quadranten unterteilt.

Die Koordinaten eines Punktes P in der Ebene erhält man, indem man von \(P\) aus das Lot auf die Achsen fällt. Die Fußpunkte geben dann die \(x\)-Koordinate \(x_P\) bzw. die y-Koordinate \(y_ P\) des Punktes \(P\) an. Wir schreiben \(P=(x_P,y_P)\), um die Lage des Punktes \(\)P\(\) anzugeben. Der Ursprung \(\)O\(\) hat daher die Koordinaten \(\)O=(0,0)$$.
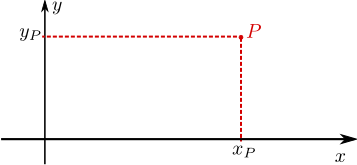
So wie jeder Punkt nach Festlegung eines Koordinatensystems eindeutige x- und y-Koordinaten besitzt, wird auch durch die Angabe der Koordinaten in der Ebene eindeutig ein Punkt festgelegt. Zu einem Zahlenpaar \((x_Q,y_Q)\in \mathbb {R}^2=\mathbb {R}\times \mathbb {R}\) gibt es genau einen Punkt Q in der Ebene, so dass \(Q=(x_ Q,y_ Q)\). Dass wir die Lage eines Punktes mit genau zwei Zahlen beschreiben können, liegt daran, dass die Ebene zweidimensional ist. Es ist möglich und auch durchaus gebräuchlich, die Lage von Punkten in anderen Koordinaten anzugeben:
-
auf der Kugeloberfläche durch geographische Länge und Breite
-
in ebenen Polarkoordinaten durch den Abstand vom Ursprung und den Winkel zwischen der Verbindungslinie zum Ursprung und der x-Achse (siehe später)

Man beachte, dass man in einer Ebene auf viele verschiedene Arten kartesische Koordinatensysteme wählen kann: Man kann einerseits den Ursprung zu einem anderen Punkt verschieben, andererseits kann man auch die Achsen um den Ursprung drehen.
Nachdem man sich auf ein bestimmtes Koordinatensystem festgelegt hat, lässt sich jeder Punkt eindeutig durch die Koordinaten darstellen.
Was gewinnt man dadurch? Man kann nun Mengen in der Ebene durch Gleichungen oder Ungleichungen beschreiben. Beispielsweise liegt die Menge der Punkte \((x,y)\) mit \(x^2+y^2< 1\) im Inneren eines Kreises vom Radius 1 um den Ursprung.
Achtung! Die Sprechweise ist hier manchmal etwas unsauber. (Sehr) korrekt ist beispielsweise
"die Menge aller Punkte \((x,y)\in \mathbb {R}^2\) mit \(x^2+y^2=4\) liegt
auf einem Kreis mit Radius 2 um den Ursprung"
Oft wird man aber hören
"\(x^2+y^2=4\) ist ein Kreis mit Radius 2 um den Ursprung"
was ja schon deshalb nicht stimmen kann, weil ein Kreis eine geometrische Figur und keine Gleichung ist.
Vektoren
Vektoren im \(\mathbb {R}^2\) oder \(\mathbb {R}^3\) kann man sich als Verschiebung veranschaulichen: Zu zwei beliebigen Punkten P und Q gibt es eine Parallelverschiebung der Ebene oder des Raumes, die genau den Punkt P auf den Punkt Q schiebt. Diese Parallelverschiebung bezeichnen wir mit \(=\overrightarrow {PQ}\) und symbolisieren den Vektor durch einen Pfeil von P nach Q.
Man beachte, dass ein Vektor eine Richtung und eine feste Länge, aber keinen festen Anfangs- und Endpunkt hat. In der folgenden Abbildung ist daher \(\overrightarrow {PQ}=\overrightarrow {RS}\).

Ein spezieller Vektor ist der Nullvektor \(\overrightarrow {0}\), der einer Verschiebung entspricht, bei der nichts verschoben wird, also der identischen Abbildung: \(\vec{0}=\overrightarrow {PP}\) für alle Punkte P.
Zu einem Vektor \(\vec{v}\) gibt es immer einen gleich langen, aber entgegengesetzt gerichteten Vektor, den wir mit \(-\vec{v}\) bezeichnen. Die Verschiebung mit \(-\vec{v}\) macht die vom Vektor \(\vec{v}\) bewirkte Verschiebung rückgängig. Insbesondere ist also \(\overrightarrow {QP}=-\overrightarrow {PQ}\).
\(\overrightarrow{PQ}=\left(\begin{array}{r}q_1-p_1\\q_2-p_2\end{array}\right).\)
Analog wird nach Wahl eines Koordinatensystems im \(\mathbb{R}^3\) jeder Vektor durch ein Tripel reeller Zahlen und im \(\mathbb {R}^n\) durch ein n-Tupel reeller Zahlen beschrieben. Wir schreiben dann
\(\vec{v}=\left(\begin{array}{c}v_1\\v_2\\\vdots\\v_n\end{array}\right)\in\mathbb{R}^n.\)
Vektoren treten in vielen technischen Anwendungen auf, zum Beispiel sind Kräfte als Vektoren aufzufassen, aber auch das elektrische Feld ist eine vektorielle Größe, da es in jedem Punkt des Raumes eine Richtung und eine "Länge" (hier: die Feldstärke) hat.
Übrigens zeigt sich hier mal wieder, warum Mathematik für Ingenieurinnen und Ingenieure so wichtig ist. Ein relativ abstraktes Konzept (hier die Vektorrechnung) lässt sich in völlig verschiedenen Zusammenhängen verwenden. Wenn man einmal gelernt hat, mit Vektoren zu rechnen, kann man damit Kräftezerlegungen, elektrische Felder, Flüssigkeitsströmungen und vieles mehr behandeln.
