1.6 Funktionen
1.6 Funktionen
Funktionen bzw. Abbildungen sind ein grundlegendes Hilfsmittel zur mathematischen Beschreibung der Zusammenhänge zwischen verschiedenen Größen.
Beispiel 1: Ohmsches Gesetz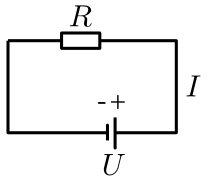 In einem elektrischen Stromkreis mit einem Widerstand \(R\) hängt die Stromstärke I von der angelegten Spannung U ab. Es gilt der Zusammenhang
In einem elektrischen Stromkreis mit einem Widerstand \(R\) hängt die Stromstärke I von der angelegten Spannung U ab. Es gilt der Zusammenhang
\(I(U)=\displaystyle\frac{U}{R}\).
Jedem Wert von \(U\) lässt sich so eine eindeutige Stromstärke \(I\) zuordnen.
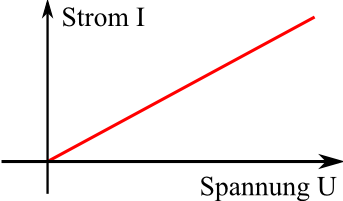
Diesen Zusammenhang kann man auch graphisch veranschaulichen durch das folgende Strom-Spannungs-Diagramm:
Tendenziell kann man sagen, dass man eher Funktion sagt, wenn \(M\) und \(N\) Mengen von Zahlen sind, während man sonst eher von Abbildungen spricht, einen echten Unterschied zwischen den beiden Begriffen gibt es aber nicht.
Wenn man eine Funktion \(f\) beschreiben möchte, gibt man meist an, was \(f\) mit den Elementen von \(M\) macht, d.h. man definiert \(f(x)\) für ein beliebiges \(x\in M\) durch eine Formel oder einen anderen Ausdruck. Oft schreibt man \(y=f(x)\), um \(f\) festzulegen, insbesondere wenn \(f:\mathbb{R}\to \mathbb {R}\) eine Funktion ist, die jeder Zahl \(x\) eine andere Zahl \(y\) zuordnet. Achtung! Dies ist ein wenig irreführend, denn in der Mathematik sind die Abbildung \(f\) und das Bild \(f(x)\) von \(x\) unter der Abbildung \(f\) zwei verschiedene Dinge.
Beispiele für Abbildungen sind die Zuordnungen
|
Matrikelnummer |
\(\longrightarrow \) |
Student/in |
|
Zahl \(n\) |
\(\longrightarrow \) |
Zahl \(n^2-1\) |
|
Datum |
\(\longrightarrow \) |
Wochentag |
|
Spannung im Draht |
\(\longrightarrow \) |
Stromstärke im Draht |
|
positive reelle Zahl \(x\) |
\(\longrightarrow \) |
reelle Zahl \(\sqrt {x}\) |
|
Kantenlänge eines Würfels |
\(\longrightarrow \) |
Volumen eines Würfels |
Wozu sind Funktionen nützlich?
Als kompakte Methode, um die Abhängigkeit einer Größe von einer (oder mehreren) anderen Größen auszudrücken. In diesem Sinne kann man eine Funktion auch als Input-Output-Relation verstehen. Man füttert einen "Input" \(x\) in einen Apparat, der einem dann auf irgendeine Weise daraus einen Output \(f(x)\) produziert. Der Definitionsbereich ist dann die Menge aller "sinnvollen" oder "vernünftigen" Inputs, während die das Bild von \(f\) die Menge aller möglichen Outputs darstellt.
Beispiel 2: Koordinatensystem
Jedem Punkt des dreidimensionalen (euklidischen) Raumes ordnet man ein Tripel \((x,y,z)\in \mathbb{R}^3\) zu, seine Koordinaten.
Umgekehrt entspricht jedem Koordinatentripel genau ein Punkt.
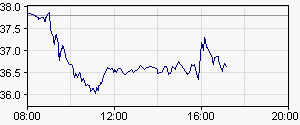
Beispiel 3: Börsenkurse
Für die Aktie der Rubotectrics AG wird im elektronischen Handel zu jedem Zeitpunkt \(t\) eines Handelstages der entsprechende Kurs \(K\) festgestellt. Das Schaubild der Funktion \(t\mapsto K(t)\) bezeichnen Börsianer als Chart und viele Versuchen mit List und Tücke aus diesen Charts Informationen über den zukünftigen Kursverlauf herauszulesen ("‘Chartanalyse"’).