10.6 Funktionsgrenzwerte und Stetigkeit
10.6 Funktionsgrenzwerte und Stetigkeit
In der Praxis hat man recht selten mit Zahlenfolgen, aber oft mit Funktionen zu tun. Daher übertragen wir den Grenzwertbegriff nun auf Funktionen.
Sei \(f:D\to \mathbb {R}\) eine Funktion und \(x_0\in \mathbb {R}\).
Man sagt, dass \(f\) für \(x\to x_0\) den Grenzwert \(a\) hat, wenn für jede Folge \(( x_ n)_{n\in \mathbb {N}}\) mit \(x_ n\in D\setminus \{ x_0 \} \) und \(\lim \limits _{n\to \infty } x_ n= x_0\) gilt:
\(\lim\limits_{n\to\infty}f( x_n)=a.\)
Man schreibt in diesem Fall
\(\lim\limits_{x\to x_0}f( x)=a.\)
Anschaulich bedeutet der Grenzübergang \(x\to x_0\), dass \(x\) der Stelle \(x_0\) beliebig nahe kommt, den Wert \(x_0\) aber nicht annimmt.
Es wird dabei vorausgesetzt, dass es eine Folge im Definitionsbereich von \(f\) gibt, die gegen \(x_0\) konvergiert.
Oft erlaubt man auch uneigentliche Grenzwerte und schreibt \(\lim \limits _{x\to x_0} f( x) =+\infty \) oder \(\lim\limits_{x\to x_0} f( x) =-\infty \), falls die Folge \(( x_ n)\) den uneigentlichen Grenzwert \(+\infty \) oder \(-\infty \) besitzt.
Aus den Rechenregeln für Grenzwerte von Folgen erhält man unmittelbar
Seien \(f\) und \(g\) zwei Funktionen, für die die Grenzwerte \(\lim\limits_{x\to x_0} f( x)\) und \(\lim \limits _{x\to x_0} g( x)\) beide existieren. Dann gilt
\(\begin{array}{rcl}\lim\limits_{x\to x_0}\left(f( x)+g( x)\right)&=&\lim\limits_{x\to x_0}f( x)+\lim\limits_{x\to x_0}g(x)\\ \lim\limits_{x\to x_0}\left(f(x)-g(x)\right)&=&\lim\limits_{x\to x_0}f( x)-\lim\limits_{x\to x_0}g( x)\\ \lim\limits_{x\to x_0}\left(f( x)\cdot g( x)\right)&=&\lim\limits_{x\to x_0}f( x)\cdot\lim\limits_{x\to x_0}g( x)\\ \lim\limits_{x\to x_0}\displaystyle\frac{f( x)}{g( x)}&=&\displaystyle\frac{\lim\limits_{x\to x_0}f( x)}{\lim\limits_{x\to x_0}g( x)}\;\;\text{falls}\;\;\lim\limits_{x\to x_0}g( x)\neq 0\\ \lim\limits_{x\to x_0}(c\cdot f( x))&=&c\cdot\lim\limits_{x\to x_0}f( x)\;\;\text{f\"ur\;\;alle}\;\;c\in\mathbb{R}\end{array}\)
Grenzwerte von Funktionen können verwendet werden, um spezielle Grenzfälle (kleine Massen, kleines Massenverhältnis, große Abstände,...) zu berechnen.
Beim idealen elastischen Stoß von zwei Massen gelten der Energie- und der Impulserhaltungssatz:
\(\begin{array}{rcl}\displaystyle\frac{1}{2}m_1u_1^2+\displaystyle\frac{1}{2}m_2u_2^2&=&\displaystyle\frac{1}{2}m_1v_1^2+\displaystyle\frac{1}{2}m_2v_2^2\\m_1u_1+m_2u_2&=&m_1v_1+m_2v_2\end{array}\)
wobei \(u_1\), \(u_2\) die Geschwindigkeiten vor dem Stoß und \(v_1\), \(v_2\) die Geschwindigkeiten nach dem Stoß sind.
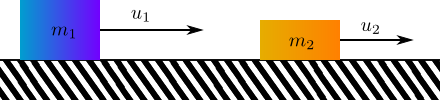
Durch algebraische Umformungen kann man aus diesen beiden Gleichungen die Geschwindigkeiten nach dem Stoß aus \(u_1\) und \(u_2\) berechnen:
\(\begin{array}{rcl}v_1&=&\displaystyle\frac{m_1u_1+m_2(-u_1+2u_2)}{m_1+m_2}\\v_2&=&\displaystyle\frac{m_1(2u_1-u_2)+m_2u_2}{m_1+m_2}\end{array}\)
Als Grenzfälle kann man beispielsweise den Fall betrachten, dass eine sehr viel größere Masse auf eine kleine trifft (\(m_2\to 0\)). Physikalisch ergibt der Grenzfall \(m_2=0\) natürlich keinen Sinn (was ist eine masselose Kugel?), aber die Geschwindigkeiten im Grenzfall \(m_2=0\)
\(\begin{array}{rcl}v_1&=&u_1\\v_2&=&2u_1-u_2\end{array}\)
sind eine gute Näherung für die Geschwindigkeiten bei \(m_2{\approx }0\)
Stetigkeit
Wenn man in einer Versuchsanordnung eine Inputgröße regeln kann, erwartet man typischerweise, dass kleine Änderungen (wenig Drehen am Regler) auch nur kleine Änderungen am Output bewirken. Diese Eigenschaft, dass eine kontinuierliche Änderung von \(x\) auch eine allmähliche Änderung von \(f( x)\) bewirkt ohne dass Sprünge auftreten, nennt man Stetigkeit. Sie ist in aller Regel die Mindestanforderung an "vernünftige" Funktionen, mit denen man technische Vorgänge beschreibt.
Es ist aber natürlich nicht so, dass diese Eigenschaft automatisch vorhanden ist. Ein anschauliches
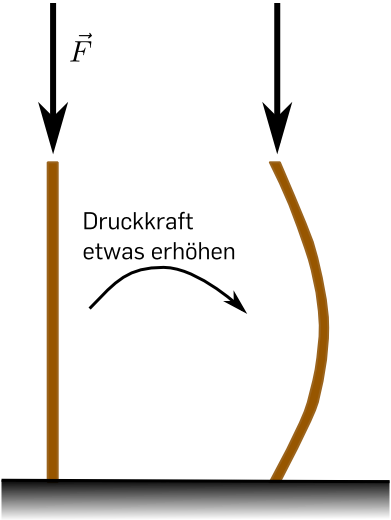
Weitere Beispiele für "natürliche" unstetige Vorgänge sind Brüche oder Rissbildungen.
\(\lim\limits_{x\to x_0}f(x)=f(x_0)\)
gilt. Die Funktion heißt stetig, wenn sie an jedem Punkt ihres Definitionsbereiches stetig ist.Summen, Differenzen, Produkte, Quotienten und Verkettungen von stetigen Funktionen sind (soweit sie definiert sind) auch wieder stetig:
-
Die Funktionen \(f+g\), \(f-g\) und \(f\cdot g\) sind stetig. Falls \(g(x)\neq 0\) für alle \(x\), dann ist auch \(f/g\) stetig
-
die Hintereinanderausführung \(g\circ f\) ist stetig (vorausgesetzt, dass \(f(x)\) für alle \(x\) im Definitionsbereich von \(g\) liegt).
Achtung! Leider gibt es nicht nur Sprungstellen, die für die Unstetigkeit einer Funktion sorgen können, sondern auch andere Effekte, insbesondere starke Oszillationen. Selbst Wertetabellen können hier ziemlich in die Irre führen.
Betrachte als Beispiel dafür die Funktion \(f( x)=\sin \left(\displaystyle\frac {\pi }{x}\right)\) mit der harmlos aussehenden Wertetabelle
| \(x\) |
\(\sin \left(\displaystyle\frac {\pi }{x}\right)\) |
|
1,0 |
0 |
|
0,5 |
0 |
|
0,4 |
1 |
|
0,3 |
-0,866 |
|
0,2 |
0 |
|
0,1 |
0 |
|
0,05 |
0 |
|
0,01 |
0 |
|
0,005 |
0 |

\(\lim\limits_{x{\to}0}\displaystyle\frac{\sin( x)}{x}=1\)
ist und dass man daher \(f\) zu einer auf ganz \(\mathbb {R}\) stetigen Funktion machen kann, wenn man an der Definitionslücke zusätzlich \(f( 0)=1\) definiert. Diese Definitionslücke ist also "hebbar", das heißt man kann sie beseitigen, indem man einen geeigneten Funktionswert "von Hand" definiert. Eine geometrische Überlegung liefert uns den oben angesprochenen Grenzwert:
\(\sin(x)\leq x\leq\tan(x)=\dfrac{\sin(x)}{\cos(x)}\)
Daraus ergibt sich\(\cos(x)\leq\displaystyle\frac{\sin( x)}{x}{\leq}1\)
und weil für \(\lim \limits _{x\to 0}\cos ( x)=\cos ( 0)=1\) ist, strebt die linke Seite der Ungleichung genau wie die rechte gegen \(1\). Damit muss auch der mittlere Ausdruck gegen \(1\) konvergieren.Der Grenzwert
\(\lim\limits_{x\to 0}\displaystyle\frac{\sin( x)}{x}=1\)
ist auch der Grund, warum man in vielen Situationen, in denen der Winkel \(x\) einigermaßen klein ist, \(\sin ( x)\) zur Vereinfachung durch \(x\) ersetzt. Der Grenzwert wird dann so interpretiert, dass für "kleine Winkel \(x\)" die Näherung \(\sin(x)\approx x\) gilt.
So wird zum Beispiel aus der Differentialgleichung \(\ddot{x}+\displaystyle\frac {g}{\ell }\sin ( x)=0\), die sich nicht exakt explizit lösen lässt durch diese Vereinfachung der harmonische Oszillator \(\ddot{x}+\displaystyle\frac {g}{\ell }x=0\), dessen Lösungen viel leichter zu bestimmen sind.
-
Kann ein Nenner Null werden?
-
Kann unter einer Wurzel etwas Negatives stehen?
-
Versucht man, den Logarithmus einer nicht-positiven Zahl zu bilden?
-
Wenn die Funktion abschnittsweise definiert ist: Passen die Abschnitte "lückenlos" zusammen?
