10.3 Konvergenz
10.3 Konvergenz
Unter allen Zahlenfolgen interessiert man sich besonders für die konvergenten Folgen, das sind diejenigen Folgen, deren Folgenglieder sich einem bestimmten Wert immer mehr annähern. Bei der Frage nach der Konvergenz geht es darum zu beschreiben, wie sich Glieder einer Folge schließlich verhalten, wenn man n immer größer macht.
Ein Behälter vom Volumen V soll mit Hilfe einer Pumpe evakuiert werden. Dazu wird mehrmals hintereinander der folgende Zyklus durchlaufen:
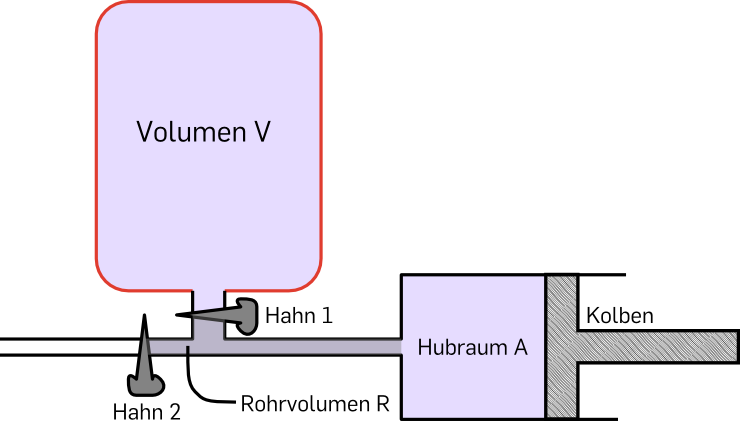
-
Hahn 1 wird geschlossen und Hahn 2 geöffnet
-
der Kolben wird herausgezogen
-
Hahn 2 wird geschlossen und Hahn 1 geöffnet
-
der Kolben wird hineingeschoben
\(p_{n+1}\cdot(V+R+K)=p_nV+p_0R\;\Rightarrow\;p_{n+1}=\displaystyle\frac{p_nV+p_0R}{V+R+K},\)
bevor Hahn 1 wieder geschlossen wird. Auf diese Weise wird der Druckverlauf im Behälter durch eine rekursive Folge beschrieben.
Von Interesse ist hier natürlich die Frage, wie klein man den Druck auf diese Weise machen kann. Für \(V=1\), \(p_0=1000\), \(K=0,2\) und \(R=0,1\) sind die ersten 50 Werte von \(p_n\) in der folgenden Graphik dargestellt:
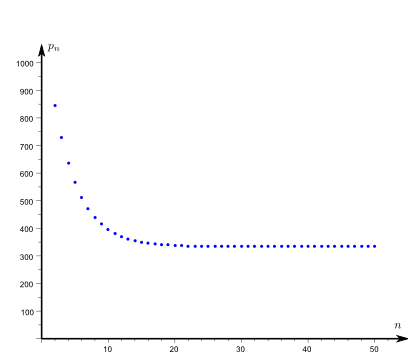
Offenbar nähert sich der Druck im Behälter immer mehr einem festen Wert \(p_{\infty }\) an. Wie man das mathematisch präzise beschreibt und wie man diesen Druck \(p_{\infty }\) bestimmt, der "schließlich" erreicht wird, werden wir in diesem Kapitel lernen.
In der Praxis wird man in vielen Fällen die Folgenglieder \(a_n\) einer konvergenten Folge \((a_ n)_{n\in \mathbb {N}}\) für großes n und den Grenzwert der Folge nicht mehr unterscheiden. In dem eben diskutierten Beispiel wird der Grenzwert des Drucks nie ganz erreicht. Trotzdem wird man davon ausgehen, dass man nur einen winzigen Fehler macht, wenn man statt \(p_{100}\) oder \(p_{1000000}\) mit dem (von n unabhängigen) Wert \(p_{\infty }\) rechnet.
Als nächstes soll nun ganz präzise beschrieben werden, was es bedeutet, dass sich die Glieder einer Folge immer mehr einem "‘Grenzwert"’ annähern.
Um die anschauliche Vorstellung mathematisch in den Griff zu bekommen, betrachtet man kleine Intervalle um eine vorgegebene Zahl herum.
\(B_{\varepsilon}(a):=\{y\in\mathbb{R};|a-y|<\varepsilon\}=(a-\varepsilon,a+\varepsilon)\)
die \(\varepsilon\)-Umgebung von \(a\).
Die Folge \((a_n)_{n\in \mathbb{N}}\) konvergiert dann gegen eine Zahl \(a\), falls es zu jedem noch so kleinen \(\varepsilon >0\) einen Index \(N=N(\varepsilon )\) gibt, so dass ab diesem Folgenindex alle Folgenglieder in der \(\varepsilon \)-Umgebung von \(a\) liegen.
Sei \(\left( x_n\right)_{n\in \mathbb {N}}\) eine Folge reeller Zahlen und \(a\) eine reelle Zahl. Dann konvergiert die Folge \(\left( x_n\right)_{n\in \mathbb {N}}\) gegen \(a\), falls es zu jeder reellen Zahl \(\varepsilon >0\) eine natürliche Zahl \(N\in \mathbb {N}\) gibt, so dass
\(|x_n-a|<\varepsilon\;\) für alle \(\;n>N.\)
Man schreibt dann
\(\lim\limits_{n\to\infty}x_n=a\;\) oder auch \(\;x_n\stackrel{n\to\infty}{\longrightarrow}a.\)
Die Zahl \(a\) nennt man den Grenzwert oder Limes der Folge.
Falls eine Folge nicht konvergiert, nennt man sie divergent.
Beispielsweise sind die Folgen \((0,1,0,1,0,1,\dots )\) oder \((1,2,3,4,5,\dots )\) oder \((1,-2,3,-4,5,-6,\dots )\) alle divergent.
Besonders häufig haben wir es mit Folgen zu tun, die gegen 0 konvergieren. Diese Folgen nennt man Nullfolgen.
