11.3 Exponentialfunktion (Fortsetzung)
Wenn man die Exponentialfunktion mit Hilfe eines Grenzwerts definiert, ist zunächst nicht klar, dass auch tatsächlich die üblichen Rechenregeln für Potenzen gelten. Daher muss man eigentlich die folgende Aussage nachweisen:
Für alle \(x,y\in \mathbb{R}\) gilt
\(\exp( x+y)=\exp( x)\cdot\exp( y).\)
Beweisidee: Wenn man von der unendlichen Summe für \(e^x\) und \(e^y\) jeweils nur einige Terme "‘mitnimmt"’, dann kann man diese (endlichen!) Summen problemlos miteinander multiplizieren. Zum Beispiel ist bis zu Termen 3. Ordnung
\(\begin{array}{rcl}&&(1+x+\displaystyle\frac{x^2}{2}+\displaystyle\frac{x^3}{6})(1+y+\displaystyle\frac{y^2}{2}+\displaystyle\frac{y^3}{6})\\&=&1+x+y+\displaystyle\frac{x^2}{2}+\displaystyle\frac{y^2}{2}+xy+\displaystyle\frac{x^3}{6}+\displaystyle\frac{x^2y}{2}+\displaystyle\frac{xy^2}{2}+\displaystyle\frac{y^3}{6}+\dots\end{array}\)
wobei die noch folgenden Terme alle mindestens von 4. Ordnung sind. Auch wenn man von der Exponentialsumme weitere Terme hinzunimmt, also \(\displaystyle\frac {x^4}{4!}\) etc. kommen beim Ausmultiplizieren nur Terme von vierter und höherer Ordnung hinzu.
Aus dem obigen Ergebnis machen wir unter Benutzung des Binomischen Satzes
\(\begin{array}{rcl}&&(1+x+\displaystyle\frac{x^2}{2}+\displaystyle\frac{x^3}{6})(1+y+\displaystyle\frac{y^2}{2}+\displaystyle\frac{y^3}{6})\\&=&1+(x+y)+\displaystyle\frac{(x+y)^2}{2!}+\displaystyle\frac{(x+y)^3}{3!}+\dots\end{array}\)
d.h. die ersten Terme der Summe sind genau die ersten Terme von \(e^{x+y}\).
Man kann mit etwas Aufwand ganz allgemein zeigen, dass dies immer noch so ist, wenn man nicht nur Terme bis zur Ordnung 3, sondern bis zu einer beliebigen Ordnung \(n\) betrachtet. Man kann sich sogar überlegen, wie man unendliche Summen miteinander multiplizieren kann und dass dann tatsächlich alle Ordnungen übereinstimmen.
Dies zeigt, dass die Exponentialfunktion die Potenzgesetze erfüllt.
Beweisidee: Wenn \(x_1\) kleiner als \(x_2\) ist, dann ist jedes Glied in der Summe für \(S_n(x_1)\) kleiner als das entsprechende Glied \(S_n(x_2)\). Entsprechend muss auch der Grenzwert \(\exp(x_1)\) kleiner sein als der Grenzwert \(\exp(x_2)\).
\(\lim\limits_{x\to\infty}\displaystyle\frac{e^x}{x^n}=+\infty\;\;\text{für jedes }n\in\mathbb{N}.\)
Für \(x\to -\infty\) klingt sie schneller ab als jede Potenzfunktion wächst:\(\lim\limits_{x\to-\infty}x^ne^x=0\;\;\text{für jedes }n\in\mathbb{N}.\)
Begründung: Für \(x>0\) ist
\(e^x=1+x+\displaystyle\frac{x^2}{2!}+\dots+\displaystyle\frac{x^{n+1}}{(n+1)!}+\dots>\displaystyle\frac{x^{n+1}}{(n+1)!}\;\Rightarrow\;\displaystyle\frac{e^x}{x^n}\geq\displaystyle\frac{x}{(n+1)!}\to+\infty\)
Für \(x<0\) ist
\(x^ne^x=(-x)^ne^{-(-x)}=\displaystyle\frac{(-x)^n}{e^{-x}}=\displaystyle\frac{1}{\frac{e^{-x}}{(-x)^n}}\)
Setzt man \(u=-x\), dann ist wegen \(\displaystyle\frac {e^u}{u^n}\to +\infty \)
\(\lim\limits_{x\to-\infty}x^ne^x=\lim\limits_{x\to-\infty}\displaystyle\frac{1}{\frac{e^{-x}}{(-x)^n}}=\lim\limits_{u\to+\infty}\displaystyle\frac{1}{\frac{e^u}{u^n}}=0.\)
☐
\(\lim\limits_{x\to\pm\infty}p(x)\cdot e^{ax}\)
mit einem Polynom \(p\) und \(a\neq 0\) immer das Verhalten der Exponentialfunktion ausschlaggebend ist.Schon mal darüber nachgedacht, warum sich ein tonnenschweres Schiff mit einem Seil festhalten lässt, das einen Poller zwei- oder dreimal umschlingt?
Die Seilreibungsformel (Euler-Eytelwein-Formel) beschreibt den Zusammenhang zwischen der ziehenden Kraft \(\vec{F}_z\) des Schiffs und der haltenden Kraft \(\vec{F}_h\) bei einem Haftreibungskoeffizienten \(\mu _H\) zwischen Seil und Poller. Dabei gilt
\(|\vec{F}_z|=|\vec{F}_h|\cdot e^{\mu_H\cdot\alpha}\)
wobei \(\alpha \) im Bogenmaß gemessene Umschlingungswinkel ist.
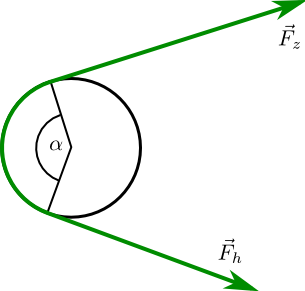
Solange die Biegesteifigkeit des Seils keine Rolle spielt, ist die Abnahme der Kraft dabei unabhängig vom Radius des Pollers!
Das schnelle Wachstum der Exponentialfunktion, bzw. das schnelle Abklingen für negative Exponenten bewirkt, dass \(|\vec{F}_ z|\) und \(|\vec{F}_ h|\) auch für moderate \(\alpha\) sehr unterschiedlich sein können.
Wenn beispielsweise das Seil zweieinhalbmal um den Poller läuft, ist \(\alpha \approx 5\pi \approx 16\), d.h. bei einem Haftreibungskoeffizient von \(\mu_H=0.15\) für die Reibung zwischen Stahlpoller und Stahlseil ist
\(|\vec{F}_z|=|\vec{F}_h|\cdot e^{0.15\cdot16}\Rightarrow|\vec{F}_h|\approx 0.09|\vec{F}_h|\)
d.h.die Haltekraft muss weniger als ein Zehntel der Zugkraft betragen.
Die Euler-Eytelwein-Formel wird ebenfalls dazu benutzt, bei einem langsam laufenden Riemenantrieb abzuschätzen, welches Drehmoment bei vorgegebener Vorspannung übertragen werden kann.
Quelle: Wikipedia.de
