12.2 Ableitungsregeln (Fortsetzung)
Besonders wichtig ist die Regel für die Ableitung verketteter Funktionen.
Seien \(I,J\subset \mathbb {R}\) offene Intervalle, \(f:I\rightarrow J\) differenzierbar an der Stelle \(x_0\in I\) und \(g:J\rightarrow \mathbb {R}\) differenzierbar an der Stelle \(y_0=f( x_0)\in J\). Dann ist auch die Hintereinanderausführung \(g\circ f:I\rightarrow \mathbb {R}\) an der Stelle \(x_0\) differenzierbar mit der Ableitung
\((g\circ f)’(x_0)=g’(f(x_0))\cdot f’(x_0).\)
Eine mathematisch nicht ganz saubere Begründung für die Kettenregel liefert die folgende Rechnung:
\(\begin{array}{rcl}\lim\limits_{h\to 0}\displaystyle\frac{g(f(x_0+h))-g(f(x_0)}{h}&=&\lim\limits_{h\to0}\displaystyle\frac{g(f(x_0+h))-g(f(x_0))}{f(x_0+h)-f(x_0)}\displaystyle\frac{f(x_0+h)-f(x_0)}{h}\\&&\to g’(f(x_0))\quad f’(x_0)\end{array}\)
Das Problem daran ist, dass für viele Werte von \(h\) eventuell \(f( x_0+h)-f( x_0)=0\) sein könnte. Dann wäre die Umformung gar nicht erlaubt.
Die Grundidee, die dahinter steckt, lässt sich aber retten, und auf etwas kompliziertere Weise kann man dann doch einen mathematisch einwandfreien Beweis der Kettenregel geben. Diesen finden Sie bei Interesse in vielen Büchern.
-
Die Funktion \(f( x)=(5x+3)^{100} \) ist die Verkettung \(f=g\circ h\) der Funktionen \(h(x)=5x+3\) und \(g(w)=w^{100}\). Wegen \(h’(x)=5\) und \(g’(w)=100 w^{99}\) ist nach der Kettenregel
\( f'(x) = g'(h(x))\cdot h'(x) = 5 \cdot (5x+3)^{99}\,. \)
-
Die Funktion \(f( x)=\cos (x^2+x^3)\) ist die Verkettung \(f=g\circ h\) der Funktionen \(h(x)=x^2+x^3\) und \(g(w)=\cos (w)\). Wegen \(h’(x)=2x+3x^2\) und \( g’(w)= -\sin (w) \) ist nach der Kettenregel
\(f’(x)=g’(h(x))\cdot h’(x)=-\sin(x^2+x^3)\cdot(2x+3x^2)\)
-
In der Wahrscheinlichkeitsrechnung tritt die Funktion \(f( x)=e^{-\frac {x^2}{2}}\) auf. Ihr Schaubild ist als Gaußsche Glockenkurve bekannt und war vor 2002 auf dem Zehnmarkschein abgebildet. Da \(f\) die Verkettung \(g\circ h\) der beiden Funktionen \(g(y)=e^ y\) und \(h(x)=-\displaystyle\frac {x^2}{2}\) ist berechnet sich die Ableitung von \(\)f\(\) als
\(f’(x)=g’(h(x)) \cdot h’(x)=e^{-\frac{x^2}{2}}\cdot(-x).\)
- Die Ableitung der allgemeinen Potenzfunktion \(p(x)=a^ x\) mit \(a>0\) lässt sich mit Hilfe der Kettenregel bestimmen, wenn man sich an die Definition \(p(x)=a^ x=e^{x\cdot \ln (a)}\) erinnert. Dann kann man \(p\) als Verkettung \(p(x)=q(r(x))\) schreiben mit \(\)q(y)=e^ y\(\) und \(\)r(x)=x\cdot \ln (a)\(\). Die beiden Ableitungen \(\)q’(y)=e^ y\(\) und \(r’(x)=\ln (a)\) sind schnell berechnet, also ist \((a^x)’=p’(x)=q’(r(x)){\cdot}r’(x)=e^{x\cdot\ln(a)}\cdot\ln(a)=a^x{\cdot}\ln(a).\)

Wir pumpen einen Luftballon auf, den wir uns idealisiert als einen Ball vom Radius \(r\) vorstellen. Wenn wir eine Pumpe benutzen, die mit einer konstanten Rate Luft in den Ballon pumpt, dann gilt für das Volumen (gemessen in Litern) \(V(t)=C\cdot t\) wobei \(\dot{V}(t)=C\) die Rate in Litern pro Sekunde angibt. Andererseits gilt für das Kugelvolumen \(V(t)=\frac{4}{3}\pi (r(t))^3\) mit einem Radius \(r(t)\), der mit der Zeit anwächst. Die Änderungsrate für diesen Radius erhält man mit Hilfe der Kettenregel, denn \(C=\dot{V}(t)=\frac{4}{3}\pi 3(r(t))^2\cdot\dot{r}(t)\;\;\Rightarrow\;\;\dot{r}(t)=\displaystyle\frac{C}{4\pi r(t)^2}\) Dem etwas erfahrenen Ingenieur oder Physiker war dieses Ergebnis schon ohne Rechnung klar, denn er interpretiert das Ergebnis als
"infinitesimale Volumenänderung = Oberfläche der Kugel mal infinitesimale Radiusänderung"
Wenn man die Ableitung einer komplizierten Funktion bestimmen möchte, sollte man zuerst überlegen, welche Struktur die Funktion hat, d.h. wie sie sich aus kleineren Teilen durch Summation, Multiplikation, Verkettung etc. zusammensetzen lässt.
Daraus ergibt sich dann, welche Regeln angewandt werden müssen und wie diese Regeln miteinander kombiniert werden.
Um die Ableitung von \( f(x)=x\cos\left(\frac{1}{1+x^2}\right)\) zu erhalten, macht man sich klar, dass \(f(x)=x\cdot g(x)\) mit \(g(x)=\cos \left(\frac{1}{1+x^2}\right)\). Also ist nach der Produktregel \(f(x)=g(x)+x\cdot g’(x)\). Die Ableitung \(g’(x)\) lässt sich wiederum mit Hilfe der Kettenregel berechnen, wenn man \(g(x)=h(k(x))\) mit \(h(x)=\cos (x)\) und \(k(x)=\frac{1}{1+x^2}\) schreibt. Damit ist
\(g’(x)=h’(k(x))k’(x)=-\sin\left(\frac{1}{1+x^2}\right)\cdot\frac{-2x}{(1+x^2)^2}\)
wobei für die Berechnung von \(k’\) noch die Quotientenregel benutzt wurde. Setzt man alles zusammen, erhält man also
\(f’(x)=\cos\left(\frac{1}{1+x^2}\right)+2\sin\left(\frac{1}{1+x^2}\right)\cdot\displaystyle\frac{x}{(1+x^2)^2}.\)
Beim Härteprüfverfahren nach Brinell wird eine Hartmetallkugel vom Durchmesser \(D\) mit einer festgelegten Prüfkraft \(F\) in die Oberfläche des zu prüfenden Werkstückes gedrückt. Anschließend wird der Durchmesser \(d\) des Eindruckes gemessen und die Brinellhärte nach der Formel
\(HBW=\displaystyle\frac{0{.}102\cdot2\cdot F}{\pi\cdot D\cdot\left(D-\sqrt{D^2-d^2}\right)}\)
bestimmt. Fasst man \(D\) und \(F\) als feste Größen auf, dann ist die Härte \(HBW(d)\) eine Funktion von \(d\), die man als Verkettung der beiden Funktionen \(h(d)=\sqrt {D^2-d^2}\) und \(g(w)=\displaystyle\frac {0{.}102 \cdot 2 \cdot F}{\pi \cdot D \cdot \left(D -w \right)}\) betrachten kann.
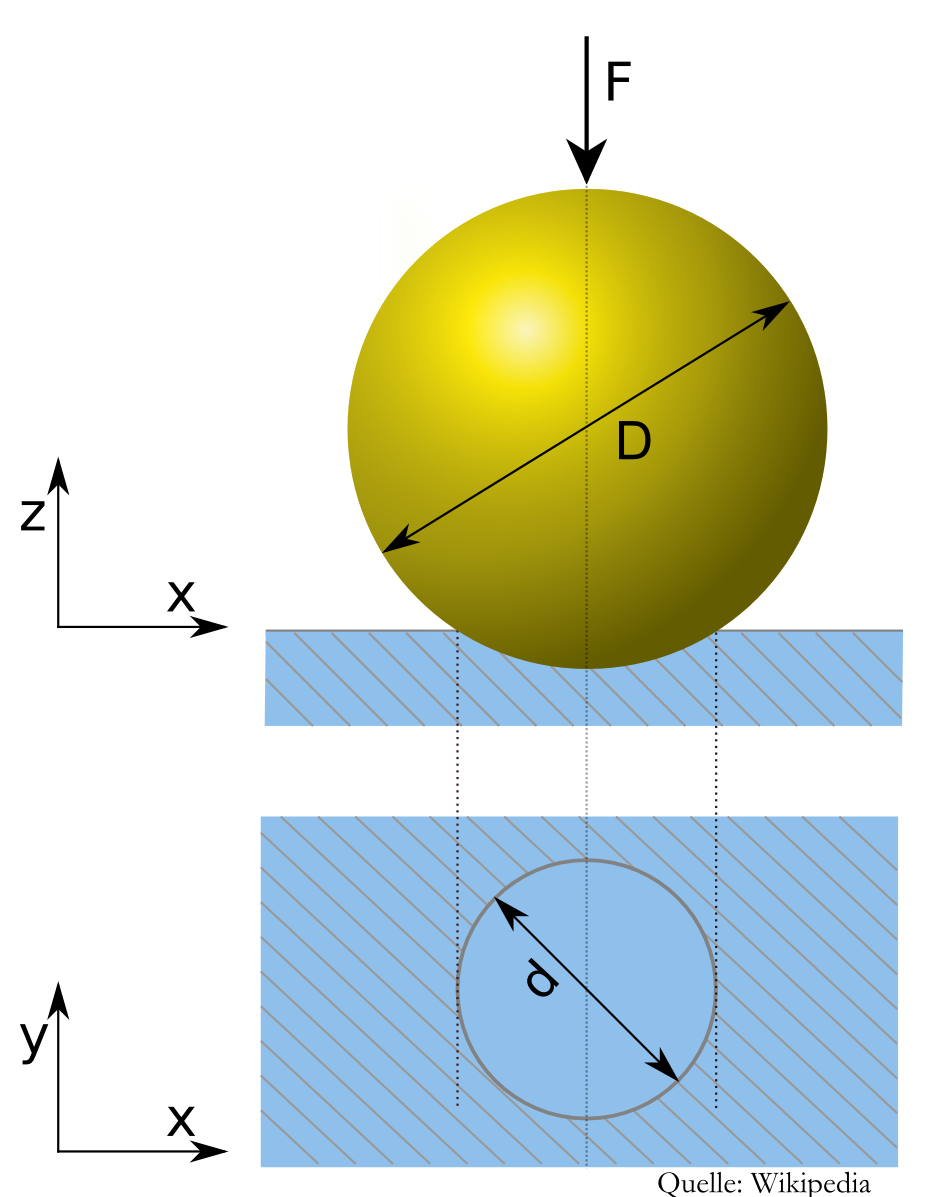
Wegen \(h=u\circ v\) mit \(v(d)=D^2-d^2\) und \(u(y)=\sqrt {y}\) braucht man schon für die Ableitung \(h\) die Kettenregel und erhält
\(h’(d)=u’(v(d))v’(d)=\displaystyle\frac{1}{2\sqrt{D^2-d^2}}(-2d)=-\displaystyle\frac{d}{\sqrt{D^2-d^2}}.\)
Daraus ergibt sich unter erneuter Anwendung der Kettenregel\( HBW’(d)=g’(h(d))\cdot h’(d)=\displaystyle\frac{0{.}102\cdot 2\cdot F}{\pi\cdot D\cdot\left(D-\sqrt{D^2-d^2}\right)^2}\left(-\displaystyle\frac{d}{\sqrt{D^2-d^2}}\right)\)
