3.1 Darstellung von Geraden (Fortsetzung)
3.1 Darstellung von Geraden (Fortsetzung)
Zwei Punkte P und Q in der Ebene mit Ortsvektoren \(\vec{p}\) und \(\vec{q}\) legen eindeutig eine Gerade fest, die durch diese beiden Punkte verläuft. Ein Punkt \(X\) mit dem Ortsvektor \(\vec{x}\) liegt genau dann auf der Geraden, wenn \(\vec{x}\) die Darstellung
\(\vec{x}=\vec{p}+s(\vec{q}-\vec{p})\)
besitzt. Dabei darf der Parameter s alle reellen Werte annehmen.
Andersherum betrachtet: Wenn s alle reellen Zahlen durchläuft, dann liefert \(\vec{x} = \vec{p} + s (\vec{q} -\vec{p})\) die Ortsvektoren von allen Punkten, die auf der Geraden durch P und Q liegen.
Dasselbe gilt, wenn man einen Punkt P und einen Richtungsvektor \(\vec{u} \in \mathbb {R}^2\) gegeben hat, wobei \(\vec{u}\neq \vec{0}\). Für alle Punkte X auf der Geraden ist dann \(\overrightarrow {PX}\) parallel zum Vektor \(\vec{u}\).
\(\vec{x}=\vec{p}+s\vec{c},\;\; s\in\mathbb{R}\)
auf einer Geraden durch P parallel zu \(\vec{c}\).
Da in beiden Fällen die Gerade dadurch dargestellt wird, dass ein Parameter (hier: s) alle möglichen Werte durchläuft, nennt man diese Formen Parameterdarstellungen von Geraden.
Geogebra-Applet: Punkt-Richtungsform einer Geraden
Die beiden Darstellungen kann man auch in Koordinaten schreiben:
Die Zwei-Punkte-Form lautet dann
\(\left(\begin{array}{r}x_1\\x_2\end{array}\right)\; = \;\left(\begin{array}{r}p_1\\p_2\end{array}\right)+s\cdot\left(\begin{array}{r}q_1-p_1\\q_2-p_2\end{array}\right)\)
Die Punkt-Richtungs-Form hat die Gestalt
\(\left(\begin{array}{r}x_1\\x_2\end{array}\right)\; = \; \left(\begin{array}{r}p_1\\p_2\end{array}\right)+s\cdot\left(\begin{array}{r}c_1\\c_2\end{array}\right)\)
-
Die Gerade durch die beiden Punkte P=(2,1) und Q=(-3,2) hat die Gleichung
\(\left(\begin{array}{r}x_1\\x_2\end{array}\right)=\left(\begin{array}{r}2\\1\end{array}\right)+s\cdot\left(\begin{array}{r}-5\\1\end{array}\right)\)
-
Die Gerade durch den Punkt P=(2,1), die parallel zu \(\vec{c}=\left(\begin{array}{r} -2\\ 3 \end{array}\right)\) ist, hat die Darstellung
\(\left(\begin{array}{r}x_1\\x_2\end{array}\right)=\left(\begin{array}{r}2\\1\end{array}\right)+s\cdot\left(\begin{array}{r}-2\\3\end{array}\right)\)
Geraden im \(\mathbb {R}^3\)
Zunächst gibt es die gerade eben eingeführten Zwei-Punkte-Form und Punkt-Richtungsform auch für Geraden im \(\mathbb {R}^3\). Sie lauten dort
\(\begin{array}{rcl}\left(\begin{array}{r}x_1\\x_2\\x_3\end{array}\right)&=&\left(\begin{array}{r}p_1\\p_2\\p_3\end{array}\right)+s\cdot\left(\begin{array}{r}q_1-p_1\\q_2-p_2\\q_3-p_3\end{array}\right)\qquad\;\text{Zwei-Punkte-Form}\\ & & \\ \left(\begin{array}{r}x_1\\x_2\\x_3\end{array}\right)&=&\left(\begin{array}{r}p_1\\p_2\\p_3\end{array}\right)+s\cdot\left(\begin{array}{r}c_1\\c_2\\c_3\end{array}\right)\qquad\;\text{Punkt-Richtungs-Form}\end{array}\)
Außer dass alle Vektoren nun eine dritte Komponente besitzen, ändert sich also überhaupt nichts. Wir können auf diese Weise auch ohne Probleme Geraden im \(\mathbb {R}^n\) definieren, auch wenn wir uns diese nicht mehr anschaulich vorstellen können.
Es gibt im \(\mathbb {R}^3\) allerdings eine neue Form, mit der man Geraden unter Benutzung des Vektorprodukts darstellen kann. Betrachte dazu eine Gerade, die durch einen Punkt \(A\) verläuft und den Richtungsvektor \(\vec{c}\) besitzt. Wenn \(P\in \mathbb {R}^3\) ein beliebiger Punkt ist, dann ist der Vektor \(\overrightarrow {AX}=\overrightarrow {PX}-\overrightarrow {PA}\) genau dann parallel zu \(\vec{c}\), wenn \(\overrightarrow {AX} \times \vec{c}= 0\) ist, d.h. \((\overrightarrow {PX}-\overrightarrow {PA})\times \vec{c}= 0\).
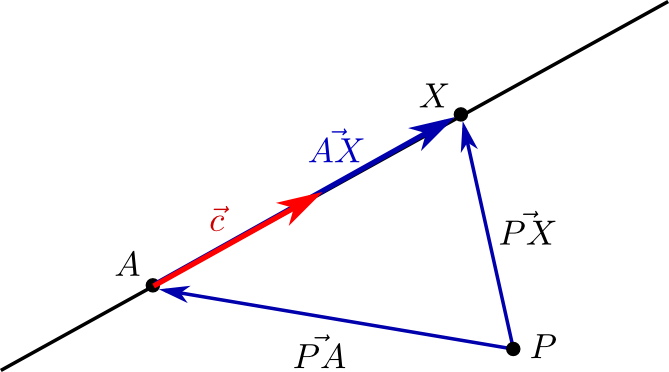
Daraus erhalten wir nun eine weitere Möglichkeit, wie man eine Gerade im \(\mathbb {R}^3\) analytisch darstellen kann.
\(\overrightarrow{PX}\times\overrightarrow{c}=\overrightarrow{PA}\times\vec{c}\)
Diese Form heißt Momentengleichung der Gerade.
